デジタル大辞泉
「対応」の意味・読み・例文・類語
出典 小学館デジタル大辞泉について 情報 | 凡例
Sponserd by 
たい‐おう【対応】
- 〘 名詞 〙
- ① 互いに向かい合うこと。相対すること。〔和漢大辞典(1919)〕
- ② ある一つの物事が、他の種類、範疇の物事に対して、対立、上位・下位、並列などの関係にあること。
- [初出の実例]「最初は『裸像』といふ同人雑誌へ、つぎは『驢馬』といふ同人雑誌へ、最後にはいろんなプロレタリヤ的な新聞雑誌へ書いた。第一部、第二部、第三部が、それに対応するわけではないが」(出典:中野重治詩集(1935)〈中野重治〉序)
- ③ 二つの異なるものや性質が、よくつり合いのとれていること。
- ④ 相手の出方や状況に応じてそれにふさわしく行動すること。
- [初出の実例]「渠(かれ)が砲艦に対応(タイオウ)すべき砲台の設け甚だ乏しく」(出典:近世紀聞(1875‐81)〈染崎延房〉四)
- ⑤ 数学で、一つの集合の各要素を第二の集合の要素にそれぞれ結びつける規則。ふつう、AからBへの対応という。→関数・写像
出典 精選版 日本国語大辞典精選版 日本国語大辞典について 情報 | 凡例
Sponserd by 
出典 株式会社平凡社「改訂新版 世界大百科事典」改訂新版 世界大百科事典について 情報
Sponserd by 
対応
たいおう
correspondence
関係P(x,y)が与えられたとき、xに対してこの関係を満足するyが何個か定まる。つまり、xとyの組が関係P(x,y)を満足するとき、yはxにこの関係で対応しているという。たとえば、実数の間の関係x2+y2=1のような場合にはxが3/5ならばyは4/5と-4/5の二つがある。しかし、xが2のときは、これに対応するyは存在しない。また、x=yはxにそれ自身を対応させており、恒等対応とよばれている。
P(x,y)となるyが存在するxの全体をこの対応の定義域、そのようなxが存在するyの全体をその値域とよぶ。定義域に属する任意のxに対してただ一つのyが対応しているとき一価な対応という。このような場合xにただ一つ決まるyを対応させる写像fが定まる。すなわちP(x,y)はy=f(x)と同値な関係となる。一価な対応をもって単に対応とよぶことがある。さらに値域に属する任意のyに対してただ一つのxが定まるとき、この対応は一対一対応とよばれる。これは全単射というのと同値である。いままでP(x,y)のxにyを対応させたが、逆にyにxを対応させることもできる。これをもとの対応の逆対応とよぶ。P(x,y)およびQ(y,z)によって定められる二つの対応の積は、xに対してP(x,y)かつQ(y,z)となるyが存在するようなzを対応させるものである。
[難波完爾]
出典 小学館 日本大百科全書(ニッポニカ)日本大百科全書(ニッポニカ)について 情報 | 凡例
Sponserd by 
対応【たいおう】
普通は関数の概念を拡張した写像と同義に扱われるが,もっと広く,多価関数の概念の拡張をも含む。つまり,二つの集合M,Nにおいて,MからNへの対応Γとは,Mの各元xにNの部分集合Γ(x)を定め,〈多対多〉となることを許したもの。ΓがMからNへの対応であるとき,直積(直積集合)M×Nの部分集合G={(x,y)|x∈M,y∈Γ(x)}をこの対応Γのグラフという。また,(x,y)∈Gとなるようなyが存在するxの集合D(⊆M)を対応Γの定義域といい,(x,y)∈Gとなるようなxが存在するyの集合R(⊆N)をΓの値域という。→1対1対応
出典 株式会社平凡社百科事典マイペディアについて 情報
Sponserd by 
対応
たいおう
correspondence
数学用語。関数,写像などと類似の概念で,ときに混用する。ただし,対応という場合には,必ずしも一意性を要求しない。数学的な形式としては,集合 A と B について,積集合 A×B の部分集合 R をグラフとして定義できる。このとき,集合 A に属する任意の元 x には R(x)={y|(x,y)∈R} の各点が対応するわけである。主として,代数幾何学で R が曲線であるときのように,多対多の対応を論じる必要のある場合に用いる。
出典 ブリタニカ国際大百科事典 小項目事典ブリタニカ国際大百科事典 小項目事典について 情報
Sponserd by 
普及版 字通
「対応」の読み・字形・画数・意味
出典 平凡社「普及版 字通」普及版 字通について 情報
Sponserd by 


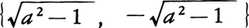 が定まり,実数から実数へ,一つの対応ができる。ΓがAからBへの対応であるとき,直積A×Bの部分集合{(a,b)|a∈A,b∈Γ(a)}を考えることができ,この集合を対応Γの
が定まり,実数から実数へ,一つの対応ができる。ΓがAからBへの対応であるとき,直積A×Bの部分集合{(a,b)|a∈A,b∈Γ(a)}を考えることができ,この集合を対応Γの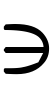 Γ(a)であるようなAの元a全体のつくる部分集合⊿(b)={a∈A|Γ(a)
Γ(a)であるようなAの元a全体のつくる部分集合⊿(b)={a∈A|Γ(a)