フェルマーの予想（読み）ふぇるまーのよそう

日本大百科全書(ニッポニカ)

フェルマーの予想
ふぇるまーのよそう

17世紀フランスの数学者フェルマーは、近代的整数論の始祖とされるが、そのフェルマーが予想し、長い間、未解決であった整数論上の難問をフェルマーの予想、またはフェルマーの問題という。フェルマーは1637年ころディオファントスの『算数論』のバシェClaude Gaspard Bachet de Méziriac（1581―1638）によるラテン語訳を読み、気づいた事柄をその欄外の余白に記入していた。ピタゴラス数、すなわち
　　x²+y²＝z²
の自然数解を記述した部分の欄外に次のような書き込みがある。「なお、立方を二つの立方に、あるいは四乗を四乗に分かつこと、そして一般に平方を超える不定のべきに対する何者も同一の名の二つのものに分かつことはできない。そのことの驚くべき証明を私は確かに暴いてしまったのだが、これを余白の狭さは受け入れなかった」
　これを現代の記法で述べるならば、「nを2より大なる自然数とすると、不定方程式xⁿ+yⁿ＝zⁿは自然数解をもたない」となる。nが4のときの証明は別のところで述べているが、一般の証明は公表されなかった。知人に結果を誇った形跡もないところをみると、証明できたと思ったのが勘違いだと気づいたのであろう。

　この問題が世に知られて以来、数多くの数学者、たとえばガウス、オイラー、ルジャンドルらがその証明に挑戦したが、以下に述べるような部分的結果を得たにとどまった。n＝3の場合はオイラー、n＝5の場合はルジャンドル、n＝7の場合はラメによってフェルマーの予想が肯定的に証明された。

　この問題に関して初めて一般的な結果を得たのはフランスの女性数学者ソフィー・ジェルマンSophie Germain（1776―1831）であろう。彼女の得た結果を述べる前に、まず、フェルマーの予想を本質的に扱いの異なる二つの場合に分類しておく。フェルマーの予想はnが素数pである場合を扱えば十分なので、今後n=pとする。xyzがpと素という条件がついた場合を「第一の場合」、xyzがpで割り切れるという条件のついた場合を「第二の場合」とよぶ。このときソフィー・ジェルマンの定理は次のように述べられる。「pが2p+1も素数であるような奇素数であればフェルマーの予想の第一の場合は正しい」
　その後、証明をさらに精密にしてルジャンドルは
　　4p+1,8p+1,10p+1,14p+1,16p+1
のいずれかが素数であれば、奇素数pに対してフェルマーの予想の第一の場合は正しい、という定理に拡張した。フェルマーの予想についての研究史上、未解決の段階でのもっとも輝かしい成果はクンマーによって得られた。その成果の一つを述べる。

　正則な素数p、すなわちベルヌーイ数
　　B₂,B₄,…… ,B_2m
　　　 m＝(p-3)/2
の分子がすべてpで割れない素数pに対してフェルマーの予想は正しい。100以下の素数で正則でないものは37,59,67の3個だけである。ただ、正則でない素数が無数に存在することは証明されているが、正則素数が無数に存在するかどうかは、いまだわかっていない。

　クンマーの手法を改良することによって、たとえば、
　　k^p-1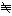1　(mod p²)
が2≦k≦43なるいずれかのkに対して成り立てば、フェルマーの予想の第一の場合は指数pに対して正しいことが知られている。この判定法を用いて、pが何億という範囲まで第一の場合が正しいことが知られている。第二の場合も、何万という大きさまでは、さまざまな判定法があって正しいことが知られている。なお、クンマーの編み出した考え方からイデアルという概念が発達し、代数的整数論のなかで大きなウェイトを占めている。

［足立恒雄］

　フェルマーがこの難解な問題を提起してから約360年後の1994年、プリンストン大学教授のワイルズAndrew Wiles（1953―　）によって問題の証明が完成された。1995年その証明が正しいことが確認され、これによりフェルマーの予想は「フェルマーの定理」となった。

［編集部］

[参照項目] | イデアル | 不定方程式

出典　小学館　日本大百科全書(ニッポニカ)