精選版 日本国語大辞典 「ブール代数」の意味・読み・例文・類語
改訂新版 世界大百科事典 「ブール代数」の意味・わかりやすい解説
ブール代数 (ブールだいすう)
Boolean algebra
G.ブールが論理計算のために導入した概念であり,今日では束,または環のことばで述べられるのがふつうである。まず論理計算との関連を見よう。一つの集合Mの元について述べられた条件の集りLについて,条件xを満たすMの元の集合をMxで表し,Mx=Myのときx=yがあると考えることにする。このとき,〈xかつy〉を満たすMの元の集合はMx∩Myであるから,〈xかつy〉をx∩yで表すことにする。同様の理由で,〈xまたはy〉をx∪yで表す。Lは考えうる条件全部とは限らないが,次の条件を満たすものとしよう。(1)x∈Lならば,xの否定x∈L,(2)x,y∈Lならばx∩y,x∪yはともに∈L。この場合,Mx≧Myのときx≧yと定めれば,Lは順序集合になり,x∩yは{z∈M|z≦x,z≦y}の最大元,x∪yは{z∈M|z≧x,z≧y}の最小元となり,∩,∪によりLに束の構造が入る。Mx
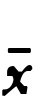 は空集合だから,x∩xはLの最小元である。Mx
は空集合だから,x∩xはLの最小元である。Mx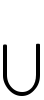
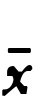 =Mだから,x∪xはLの最大元になる。したがって,Lは次の条件(1),(2),(3)を満たす束である。(1)Lには最大元Iおよび最小元0がある。(2)x∈Lならば,適当な元x′により,x∪x′=I,x∩x′=0。このx′はxの相補元と呼ばれる(xの否定xがxの相補元である)。(3)x,y,z∈Lならば,x∩(y∪z)=(x∩y)∪(x∩z)。
=Mだから,x∪xはLの最大元になる。したがって,Lは次の条件(1),(2),(3)を満たす束である。(1)Lには最大元Iおよび最小元0がある。(2)x∈Lならば,適当な元x′により,x∪x′=I,x∩x′=0。このx′はxの相補元と呼ばれる(xの否定xがxの相補元である)。(3)x,y,z∈Lならば,x∩(y∪z)=(x∩y)∪(x∩z)。
一般に,この条件(1)~(3)を満たす束をブール束,またはブール代数という。次の(3)′により(1),(2),(3)′を条件にしても同等である。(3)′a<x<b(a,b,x∈L)ならばxのa,bに関する相対補元y(定義は,x∩y=a,x∪y=bとなる元y)が存在し,かつただ一つに限る。
環のことばでは次のように述べることができ,そのときLはブール環であるという。(1)Lは単位元をもつ環であり,(2)すべてのx∈Lについてx2=x。この条件から,(3)x∈Lならばx+x=0,(4)x,y∈Lならばxy=yxが得られる。なぜなら,(1)により,4x=4x2=(x+x)2=x+x。ゆえに2x=0。また,x+y=(x+y)2=x2+xy+yx+y2=x+y+xy+yx。ゆえにxy+yx=0。これと(3)とからxy=yx。
環によるものと束によるものとの関連について述べよう。ブール束Lが与えられたとき,xy=x∩yによって乗法を定め,0とx∪yに関するx∩yの相対補元をx+yと定めればLはブール環になる。逆にLがブール環であれば,x∩y=xy,x∪y=x+y+xyと定めればLはブール束になるのである。
執筆者:永田 雅宜
出典 株式会社平凡社「改訂新版 世界大百科事典」改訂新版 世界大百科事典について 情報
日本大百科全書(ニッポニカ) 「ブール代数」の意味・わかりやすい解説
ブール代数
ぶーるだいすう
イギリスの数学者G・ブールが論理計算の場として導入した代数系で、論理学、集合論への適用だけでなく、コンピュータの回路設計など、その応用範囲は広い。理論は二値の述語論理で、論理式全体の集合をFとし、任意の論理式pとqについて、p=qとはp≡q(pとqは同値)が成り立つこととする。三つの論理演算p∨q(pあるいはq)、p∧q(pかつq)、~p(pの否定)を考える。このとき次の式が成り立つ。
(1) p∨q=q∨p p∧q=q∧p
(2) p∨(q∨r)=(p∨q)∨r
p∧(q∧r)=(p∧q)∧r
(3) (p∨q)∧q=q
(p∧q)∨q=q
(4) (p∨q)∧r
=(p∧r)∨(q∧r)
(p∧q)∨r
=(p∨r)∧(q∨r)
論理式pとqのいかんにかかわらず、
p∨~p=q∨~q,
p∧~p=q∧~q
である。そこで、p∨~p,p∧~pをそれぞれ1(真)と0(偽)で表すと、
(5) p∨~p=1 p∧~p=0
である。これを一般化する。すなわち、集合Bは少なくとも二つの元1と0を含み、Bの二つの元xとyには、x∨y,x∧y,x*というBの元が定義されていて、次の条件を満たすとする。ここでx*はxの補元を表す。
(1) x∨y=y∨x x∧y=y∧x
(2) x∨(y∨r)=(x∨y)∨r
x∧(y∧r)=(x∧y)∧r
(3) (x∨y)∧y=y
(x∧y)∨y=y
(4) (x∨y)∧r
=(x∧r)∨(y∧r)
(x∧y)∨r
=(x∨r)∧(y∨r)
(5) x∨x*=1 x∧x*=0
このときBをブール代数といい、二項演算x∨y,x∧yと一項演算x*をブール演算という。この条件(1)~(5)から、ド・モルガンの法則
(x∨y)*=x*∧y*,(x∧y)*=x*∨y*
が導かれる。また、x≦yをx∧y=x(これはx∨y=yと同値)のこととすれば、Bは順序集合となり、x∨y(x∧y)は、xとyより大(小)なる最小(最大)の元になる。前の述語論理では、論理式pとqについて、p≦qはp→q(pならばq)のことである。
次に集合計算について考える。集合Aの部分集合の全体をP(A)とする。P(A)の元x、yはともにAの部分集合である。これらのx、yに対して、x∨y,x∧y,x*をそれぞれ、xとyの和集合、共通集合、Aに対するxの補集合とすれば、それらはそれぞれAの部分集合となり、P(A)の元である。1としてAを、0として空集合をとれば、それらはまたP(A)の元である。そして、これらの演算はまた条件(1)~(5)を満たす。したがって、P(A)はこれらのブール演算に関してブール代数である。この場合、x≦yは、集合の包含関係x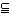 yと一致する。
yと一致する。
[西村敏男]
ブリタニカ国際大百科事典 小項目事典 「ブール代数」の意味・わかりやすい解説
ブール代数
ブールだいすう
「ブール束」のページをご覧ください。
出典 ブリタニカ国際大百科事典 小項目事典ブリタニカ国際大百科事典 小項目事典について 情報
春になって暖かくなりかけた頃、急に寒さが戻って、地面などがまた凍りつく。《 季語・春 》[初出の実例]「七瀬御秡 同晦日也。〈略〉雪汁いてかへる」(出典:俳諧・誹諧初学抄(1641)初春)...

