改訂新版 世界大百科事典 の解説
ボース=アインシュタイン凝縮 (ボースアインシュタインぎょうしゅく)
Bose-Einstein condensation
相互作用のないボース粒子N個が体積Vの容器の中に入れられているとしよう。粒子と壁との衝突は弾性衝突であるとすると,各粒子のエネルギーεは時間的に一定になる。粒子の質量をm,運動量をpとすると,ε=p2/2mである。ボルツマンの統計力学(古典統計力学)によれば,この粒子集団が絶対温度Tの熱平衡状態にあるとき,運動量p=(px,py,pz)の各成分がpαとpα+dpα(α=x,yまたはz)の間にあるような粒子の数は,マクスウェル=ボルツマン分布,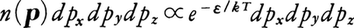 で与えられる。ここにn(p)は分布関数,kはボルツマン定数である。これによれば,εが小さいほどn(p)は大きくなる。しかし最低エネルギーε0=0(すなわちp=0)をとる粒子の数がずぬけて大きくなることは,絶対0度でないかぎりあり得ない。こうした古典論が成り立つのは高温ないし低密度の場合,すなわち,
で与えられる。ここにn(p)は分布関数,kはボルツマン定数である。これによれば,εが小さいほどn(p)は大きくなる。しかし最低エネルギーε0=0(すなわちp=0)をとる粒子の数がずぬけて大きくなることは,絶対0度でないかぎりあり得ない。こうした古典論が成り立つのは高温ないし低密度の場合,すなわち,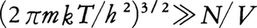 のときである(hはプランク定数)。これに反し,上式の両辺の大きさが接近してくると,粒子の量子性が顕在化してくる。量子論では,箱の中で粒子のとり得るエネルギーの値は連続量ではなく,とびとびになって,運動エネルギーの最低値はε0=(3/8m)(h/L)2になる(Lは立方体の箱の1辺の長さ)。巨視系ではε0≅0としてよい。エネルギー固有値がεであるような一つの量子状態に存在する粒子数の平均値は,ボース=アインシュタイン分布により,
のときである(hはプランク定数)。これに反し,上式の両辺の大きさが接近してくると,粒子の量子性が顕在化してくる。量子論では,箱の中で粒子のとり得るエネルギーの値は連続量ではなく,とびとびになって,運動エネルギーの最低値はε0=(3/8m)(h/L)2になる(Lは立方体の箱の1辺の長さ)。巨視系ではε0≅0としてよい。エネルギー固有値がεであるような一つの量子状態に存在する粒子数の平均値は,ボース=アインシュタイン分布により,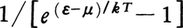 になる(μは化学ポテンシャル)。よほどの低温,高密度にならないうちはμ<ε0であり,どの量子状態も格別多数の粒子に占められることにならない。巨視系では(2πmkT/h2)3/2の値が(N/V)×0.3828にまで下がるとμ=ε0となり,それ以下の温度(ないし高密度)では,最低エネルギーε0をとる粒子数がずぬけて大きくなる。ずぬけて大きくなるという意味は,アボガドロ数~6×1023と比較できる大きさ(例えばその1万分の1くらい)になるということである。これは最低エネルギーε0の状態に巨視的な数の粒子が落ち込んでしまったことを意味し,この現象をボース=アインシュタイン凝縮,あるいはボース凝縮と呼んでいる。ボース粒子集団の基底状態は全粒子がε0に落ち込んでしまった状態になっているが,有限温度でも,十分低温であるかぎり,ε0を占めている粒子の数が巨視的大きさを保っているということがボース=アインシュタイン凝縮なのである。凝縮ということばは,エネルギー準位を書いてみたとき,そこにばらまかれた粒子の分布が最低準位ε0にたまるというイメージに由来する。
になる(μは化学ポテンシャル)。よほどの低温,高密度にならないうちはμ<ε0であり,どの量子状態も格別多数の粒子に占められることにならない。巨視系では(2πmkT/h2)3/2の値が(N/V)×0.3828にまで下がるとμ=ε0となり,それ以下の温度(ないし高密度)では,最低エネルギーε0をとる粒子数がずぬけて大きくなる。ずぬけて大きくなるという意味は,アボガドロ数~6×1023と比較できる大きさ(例えばその1万分の1くらい)になるということである。これは最低エネルギーε0の状態に巨視的な数の粒子が落ち込んでしまったことを意味し,この現象をボース=アインシュタイン凝縮,あるいはボース凝縮と呼んでいる。ボース粒子集団の基底状態は全粒子がε0に落ち込んでしまった状態になっているが,有限温度でも,十分低温であるかぎり,ε0を占めている粒子の数が巨視的大きさを保っているということがボース=アインシュタイン凝縮なのである。凝縮ということばは,エネルギー準位を書いてみたとき,そこにばらまかれた粒子の分布が最低準位ε0にたまるというイメージに由来する。
二次元や一次元の世界(平面内や1直線上でしか運動できないボース粒子系)ではボース=アインシュタイン凝縮は起こらない。基底状態が凝縮しているのは当然であるが,どんな低温でも,完全にT=0でないかぎりこの凝縮は崩れてしまうのである。
ボース=アインシュタイン凝縮の例として,4Heの液体の超流動状態があげられることがある。しかし4He原子の間には弱いファン・デル・ワールス引力のほかに,お互い電子雲の中にめり込めないという性質があり,相互作用無視というわけにいかない。しかしそれでも,ある温度Tc以下で最低エネルギーの1粒子状態への凝縮が起こるという性質は保持されていて,これが超流動の前提となっていることは確かである。4Heの例では,基底状態でさえ,p=0以外の運動量をもつ粒子が存在している。しかしまたそれゆえにp=0に凝縮した粒子集団の波動関数に明確な位相を生み出すことが可能になり,この位相の確定ゆえに超流動が発生するのである。ボース=アインシュタイン凝縮即超流動ではないが,この凝縮のないところにボース液体の超流動はあり得ない。
→超流動
執筆者:伊豆山 健夫
出典 株式会社平凡社「改訂新版 世界大百科事典」改訂新版 世界大百科事典について 情報
日本大百科全書(ニッポニカ) の解説
ボース‐アインシュタイン凝縮
ぼーすあいんしゅたいんぎょうしゅく
Bose-Einstein condensation
粒子がボース‐アインシュタイン統計に従うとき、エネルギーεをもつ粒子数の平均値はボース分布関数
f(ε)=1/[e(ε-μ)/kT-1]
で与えられる。kはボルツマン定数、μは化学ポテンシャルである。ボース粒子の理想気体で温度を下げると、系の次元や密度によっては有限の温度T0以下でμが0になることがある。この場合、T0以下の温度で最低エネルギー(ε=0)の状態の粒子数は限りなく大きくなりうるので、莫大(ばくだい)な数の粒子がε=0の状態に「落ち込む」ようになる。これをボース‐アインシュタイン凝縮という。1925年にアインシュタインが、量子集団がもつこの奇妙な性質に気づいた。
電子、陽子、中性子などの素粒子はフェルミ粒子であるが、それらが偶数個集まってできた原子はボース粒子とみなすことができる。たとえばヘリウム4の原子は、原子核に陽子と中性子が2個ずつ、その周りに2個の電子が存在するので、総計6個のフェルミ粒子があり、全体としてボース粒子としてふるまう。液体ヘリウム4は、絶対温度2.17K以下の温度において超流動となる。実際には、液体ヘリウム4には相互作用があってボース粒子の理想気体ではないが、この超流動現象はボース‐アインシュタイン凝縮の例であるといえる。
1995年、コロラド大学のC・E・ワイマンらのグループは、レーザーを用いた巧妙な方法でルビジウム原子を絶対零度まであと1億分の2℃という極低温にまで冷却し、ボース‐アインシュタイン凝縮の観測に成功した。凝縮相にある原子気体は、これまでにはなかった新しい物質相であり、精力的に研究が続けられている。
[小形正男]
化学辞典 第2版 の解説
ボース-アインシュタイン凝縮
ボースアインシュタインギョウシュク
Bose-Einstein condensation
ボース統計に従う粒子からなる理想気体(粒子数N,体積V)は,ある絶対温度 Tc 以下(Tc は2.612(2πmkTc)3/2/h3 = N/Vから決まる.mは粒子の質量,kはボルツマン定数,hはプランク定数)では,エネルギー最低の量子状態にある平均粒子数がNと同程度の巨視的量となっている.粒子間の相互作用が無視できないような系の場合も含めて,ある一つの量子状態に存在する平均粒子数が巨視的量となっているとき,系はボース-アインシュタイン凝縮またはボース凝縮を起こしているという.この現象はA. Einstein(アインシュタイン)によってはじめて指摘されたもので,その後,F. London(ロンドン)によって液体 4He がT = 2.18 K で示す転移現象の模型として提唱された.液体 4He には二つの相,すなわち,HeⅠとHeⅡがあり,これらのうち,低温の相HeⅡはボース-アインシュタイン凝縮を起こした相と考えられる.
出典 森北出版「化学辞典(第2版)」化学辞典 第2版について 情報
ブリタニカ国際大百科事典 小項目事典 の解説
ボース=アインシュタイン凝縮
ボース=アインシュタインぎょうしゅく
Bose-Einstein condensation
出典 ブリタニカ国際大百科事典 小項目事典ブリタニカ国際大百科事典 小項目事典について 情報
法則の辞典 の解説
ボース‐アインシュタイン凝縮【Bose-Einstein condensation】
春になって暖かくなりかけた頃、急に寒さが戻って、地面などがまた凍りつく。《 季語・春 》[初出の実例]「七瀬御秡 同晦日也。〈略〉雪汁いてかへる」(出典:俳諧・誹諧初学抄(1641)初春)...

