ボースアインシュタイン統計（読み）ボースアインシュタイントウケイ（その他表記）Bose‐Einstein statistics

デジタル大辞泉

ボースアインシュタイン‐とうけい【ボースアインシュタイン統計】

スピンがゼロか整数の値をもつボース粒子の集まりが示す統計的性質。1924年、ボースとアインシュタインがそれぞれ独立して導出。粒子同士に相互作用はなく、一つの粒子状態をいくつもの粒子が占有できる。この統計に従う粒子系が、ある絶対温度を下回ると、すべての粒子が一つの最低エネルギーをとるボースアインシュタイン凝縮という状態になる。ボース統計。→フェルミディラック統計

出典　小学館

日本大百科全書(ニッポニカ)

ボース‐アインシュタイン統計
ぼーすあいんしゅたいんとうけい
Bose‐Einstein statistics

多数の粒子の運動を統計的に扱って、その系の性質を表現する方法の一つ。1924年にインドのボースが、プランクの放射公式を量子統計の方法で導出したときに用い、アインシュタインが物質粒子にも適用した。単にボース統計ともいう。

　量子力学では同種粒子の区別はできないので、N粒子からなる系を表す一つの量子状態は、各1粒子状態に粒子が何個ずつ入っているかによって指定される。この数を占有数という。この占有数に制限がない場合をボース統計という（一方、2個以上の粒子が同じ状態にならないという制限がある場合をフェルミ‐ディラック統計という）。

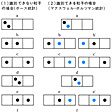
　粒子を小球とし、1粒子状態を器で表すとする。2個の球を3個の器に分ける場合、球が識別できるときには各球が三つの器のどれに入るかで3×3＝9通りが可能だが（図の(1)）、識別できないと図の(2)のように、2球とも同じ器に入る場合が3通り、別の器に入る場合が3通り、計6通りしかない。ボース統計ではこの6通りを考える（一方、フェルミ統計では後者の3通りのみが許される）。

　このようなボース統計に従う粒子をボース粒子またはボソンという。0を含む整数スピンをもつ素粒子や、光子、ヘリウム4などがボース粒子である。また格子振動やスピンの運動を量子化して得られるフォノン、スピン波（マグノン）などもボース統計に従う。

　ボース統計に従う粒子系が絶対温度Tの熱浴（物体と接触して熱のやりとりをする外界）と粒子浴（物体と接触して粒子のやりとりをする外界）に接しているとして統計力学的に扱うと、エネルギーεをもつ粒子数の平均値は
　　f(ε)＝1/[e^(ε-μ)/kT-1]
で与えられることが示される。これをボース分布関数といい、kはボルツマン定数、μは化学ポテンシャルである。光子やフォノンなど粒子数が固定されない場合、粒子浴を考える必要はなく、μは0となる。また、ボース粒子の理想気体で温度を下げると、系の次元や密度によっては有限の温度T₀以下の温度で最低エネルギー(ε＝0)の状態に、莫大(ばくだい)な数の粒子が「落ち込む」ようになる。これをボース‐アインシュタイン凝縮という。

［小出昭一郎・小形正男］

[参照項目] | アインシュタイン | フェルミ‐ディラック統計 | ボース | ボース‐アインシュタイン凝縮

ボース統計とマクスウェル-ボルツマン統…

出典　小学館　日本大百科全書(ニッポニカ)

法則の辞典

ボース‐アインシュタイン統計【Bose-Einstein's statistics】

相互作用の非常に弱い N 個の同種粒子からなる系を考えたとき，系の全粒子数∑n_j＝N，全エネルギー一定条件（∑n_jε_j＝E）という条件と，粒子の座標の置き換えによって波動関数の符号が逆転しない条件を適応すると，平衡分布は下のようになる（符号が反転するならばフェルミ‐ディラック統計＊となる）．

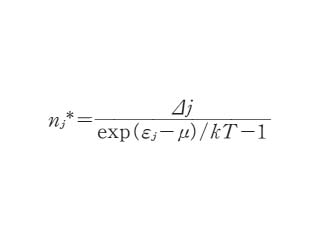
ここで ⊿j はエネルギー準位 ε_j にある状態の数，μ は化学ポテンシャルに相当する．これがボース‐アインシュタイン統計と呼ばれる．1924年にボース（S. N. Bose）とアインシュタイン（A. Einstein）がそれぞれ独立に導いたのでこの名がある．

出典　朝倉書店

化学辞典 第2版

ボース-アインシュタイン統計
ボースアインシュタイントウケイ
Bose-Einstein statistics

ボース統計ともいう．光子，スピンが0または1の中間子，重陽子あるいは ⁴He のように0または整数のスピンをもつ粒子からなる体系では，系の状態を表す波動関数が粒子の交換に対して対称的になっている．この場合，粒子はボース-アインシュタイン統計または単にボース統計に従うという．[別用語参照]量子統計力学

出典　森北出版「化学辞典（第2版）」

改訂新版　世界大百科事典

ボース=アインシュタイン統計 (ボースアインシュタインとうけい)

→量子統計

出典　株式会社平凡社「改訂新版　世界大百科事典」

ブリタニカ国際大百科事典 小項目事典

ボース＝アインシュタイン統計
ボースアインシュタインとうけい

「ボース統計」のページをご覧ください。

出典　ブリタニカ国際大百科事典 小項目事典

世界大百科事典（旧版）内のボースアインシュタイン統計の言及

【アインシュタイン】より

…24年放射を光量子気体として扱い，新しい統計的方法を提出したS.N.ボースの研究を高く評価したアインシュタインは，その方法を物質粒子の理想気体の場合に適用した。これはボース=アインシュタイン統計と呼ばれる。他方で光量子仮説は，1923年のL.V.ド･ブロイの物質波の考えを導き，それがE.シュレーディンガーの波動力学への道を用意した。…

【量子統計】より

…このことから，フェルミ粒子の場合は一つの粒子状態を占める粒子数は0または1に限られる(フェルミ=ディラック統計，またはフェルミ統計という)。一方，ボース粒子の場合は一つの粒子状態が収容できる粒子数は0,1,2,3，……と限りがない(ボース=アインシュタイン統計，またはボース統計という)。　相互作用のない多粒子系が温度Tの熱平衡状態にある場合，エネルギーεの1粒子状態jにいるフェルミ粒子の数n_jは平均して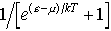，であり，ボース粒子なら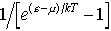，である(μは化学ポテンシャル)。…

※「ボースアインシュタイン統計」について言及している用語解説の一部を掲載しています。

出典｜株式会社平凡社「世界大百科事典（旧版）」