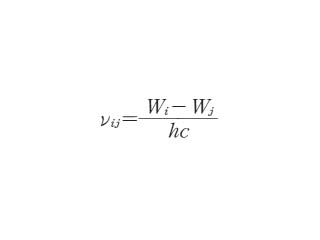リッツの結合原理（読み）りっつのけつごうげんり（その他表記）Ritz's combination principle

日本大百科全書(ニッポニカ)

リッツの結合原理
りっつのけつごうげんり
Ritz's combination principle

1908年リッツによって得られたスペクトル線に関する実験法則。原子の示すスペクトルは一般にとびとびの波長のところに現れる。これを線スペクトルとよぶ。吸収スペクトルの場合も同様であり、これらの線スペクトルは各原子に固有なものである。原子のスペクトルは波長の間に規則性をもつスペクトル系列とよばれるグループに分類できる。その一般式はリュードベリによってみいだされ、リュードベリの公式として知られている。

1/λ=R［1/(m+a)²-1/(n+b)²］
　波長λの逆数は単位長さ当りに含まれる波の数で波数（普通νで表す）とよばれるが、これは光の振動数、したがって光子のエネルギーに比例するものである。Rはリュードベリ定数、a、bは物質ごとに、また系列ごとに異なる値をとるが、m、nは整数で一つの系列に対してmは一定である。スペクトルの振動数は、いつもそれぞれ整数を含んだ二つの項の差で表される。この項をスペクトル項とよぶ。リッツは、スペクトルの波数をこれらのスペクトルの項の差として整理することができることをみいだした。これをリッツの結合原理という。

　原子が放出または吸収する光の振動数についてのこれらの法則を、古典的な理論で理解することはできない。量子論によれば原子が放出あるいは吸収する光の波数はν₁₂=(E₁-E₂)/hcで与えられる。hはプランクの定数、cは真空中の光速度、E₁、E₂はそれぞれ放出前、後あるいは吸収の後、前のエネルギー準位である。したがってν₁₂+ν₂₃=ν₁₃という関係が成立し、リッツの結合原理を量子論的に理解することができる。そのときスペクトル項はE/hcで、エネルギー準位と同じ量子数で区別されることがわかる。

［村岡光男］

[参照項目] | リュードベリ定数

出典　小学館　日本大百科全書(ニッポニカ)

法則の辞典

リッツの結合原理【Ritz's combination principle】

スペクトル線の波数 ν_ij は

で与えられる．ここで c は光速，h はプランク定数，W_i，W_j は光の放出前と放出後の各準位のエネルギーである．一般に

ν_ij＋ν_jk＝ν_ik

が成立する．これがリッツの結合原理と呼ばれる．

出典　朝倉書店

ブリタニカ国際大百科事典 小項目事典

リッツの結合原理
リッツのけつごうげんり
Ritz's combination principle

原子から放出されるスペクトルのうち，2つのスペクトル線の波数 (波長の逆数) の和または差は他のスペクトル線の波数に一致するという実験的な法則。 1908年 W.リッツにより発見された。複雑なスペクトルのなかからスペクトル系列を見出すのに利用された。また W.ハイゼンベルクはこの原理を手掛りにして行列力学を導き出した。

出典　ブリタニカ国際大百科事典 小項目事典