最新 心理学事典 の解説
カテゴリカル・データぶんせき
カテゴリカル・データ分析
categorical data analysis
クロス表cross tabulationとは,複数の離散変数を組み合わせて度数を集計した表で,分割表contingency tableともいう。たとえば76ページ表1は,余裕資金があるときにハイリスク・ハイリターンな投資をするかどうか尋ねた結果を,男女別に集計したクロス表である。
合計2155人のサンプルをまず男女で分類し,さらにリスクの高い投資をするかどうかで3分類している。各行,列の合計を周辺度数marginal frequencyといい,周辺度数の分布を周辺分布marginal distributionという。このように二つの変数からなるクロス表を二元表といい,一般にn個の変数からなるクロス表をn元表n-way tableという。
このようなクロス表の分析においては,変数間の独立性がしばしば検定される。独立性independenceとは,複数の変数の分布が互いに独立な状態を指す。表1の周辺度数のもとで性別と高リスク投資という二つの変数が独立である場合の期待値を計算すると,表2のようになる。
複数の変数が互いに独立である場合,表2のように行ごと,列ごとの分布がすべて同じになる。帰無仮説として二変数の独立を仮定し,これを検定することを独立性の検定といい,ピアソンの適合度統計量Pearson's goodness of fit statistics,χ2(カイ2乗,単にカイ2乗値とよぶことも多い)が統計量としてよく用いられる。このχ2は自由度が(r-1)(c-1)のカイ2乗分布に近似する(rは二元表の行数,cは列数)。ピアソンの適合度統計量は,期待度数が小さい場合にはカイ2乗分布からの乖離が大きくなるために,正確な検定ができない。この期待度数の問題は,独立性の検定に限らず,推定や検定を伴うカテゴリカル・データ分析に共通の問題である。帰無仮説が棄却されれば,二変数になんらかの関連があるとみなされる。
対数線形モデルlog-linear modelとは一般化線形モデルの一種で,クロス表のセル度数を予測するモデルである。一般化線形モデルgeneralized linear model(GLM)とは,以下のような共通の特徴をもつモデルの総称である。なんらかの確率分布に従う被説明変数をY,Yの期待値をE(Y)とすると,
link(E(Y))=b0+b1X1+…+bmXm
で表わされるモデルを一般化線形モデルという。ただし,linkはなんらかの関数,X1,…,Xmはm個の説明変数,b0,b1,…,bmはパラメータである。たとえば回帰分析や分散分析もGLMの一種であり,Yが正規分布すると仮定し,linkを単なる等値とした場合にあたる。対数線形モデルも,Yをセル度数としてポアソン分布を仮定し,linkを自然対数とした場合のGLMである。
対数線形モデルは,セルの数の多いクロス表の分析に用いられることが多い。三変数以上の多元表に関して,変数間の関連の有無だけを検討する場合,階層的対数線形モデルstratified log-linear modelがよく使われる。対数線形モデルではカテゴリカル変数を因子factorとよぶこともある。たとえば,三つの変数A,B,Cからなる三元表において,変数間の関連には,⑴三つの変数がすべて相互に独立([A][B][C]),⑵AとBは関連しているが,CはAともBとも独立([AB][C]),⑶AとB,BとCは関連しているが,AとCはBの効果を統制すると独立([AB][BC],AとCは条件付き独立conditional independence),⑷三変数は相互に関連([AB][AC][BC],対連関モデルともいわれる),⑸三変数の間に2次の交互作用効果がある場合([ABC],三元表の場合はこれが飽和モデルsaturated model)の五つのタイプの関連がありうる。階層的対数線形モデルでは,これらのタイプの関連のうち,どれが最もデータへの当てはまりが良いかを検討できる。各モデルに対して尤度比統計量likelihood ratio statistics(モデル・カイ2乗値とよばれることもある。カテゴリカル・データの分析では,L2またはG2と表記されることが多い)とその自由度を計算できるので,これらを使ってモデルを選ぶ。しかし,サンプルが著しく多い場合,飽和モデル以外のすべてのモデルは,ほとんど確実に棄却されてしまうため,サンプル・サイズの効果を考慮したモデル選択基準が推奨される。たとえば,ベイズ情報量規準Bayesian information criterion(BIC)がモデル選択の基準として用いられることもある。BICが小さいほどモデルの当てはまりは良いので,検討しているモデルのうちで最もBICの小さなモデルが,最も当てはまりが良いと考えられる。たとえば,表3に関して階層的対数線形モデルを当てはめると,表4のような結果が得られる。 表4を見ると,[AB][AC][BC]のp値が0.61で棄却できないのがわかる。またBICも最小なので,当てはまりの良さからいえば,[AB][AC][BC]が採択される。ただし,研究テーマとの関係でどのような帰無仮説・対立仮説を設定するかによっても,採択すべきモデルは変わってくるので,機械的に最も当てはまりの良いモデルを採択してはいけない。とくに変数の数が四つ以上になったり,非階層的モデルを仮定すると,検討すべきモデルが多くなりすぎて,すべてのモデルの当てはまりの良さを比較することはほぼ不可能になる。そのため,研究上の問いや帰無仮説・対立仮説から,検討すべきモデルを絞り込むことは非常に重要である。
非階層的モデルでとくによく使われるのは,準独立モデルである。準独立モデルquasi-independence modelとは,行数と列数が同じクロス表において対角線上以外のセルに関しては二変数は独立であるが,対角線上のみは独立ではないような状態を指す。また,対数線形モデルの拡張として,パラメータ同士の積をモデルに含む対数乗法モデルlog multiplicative modelもある。これは一般化線形モデルではないが,変数同士の交互作用を簡潔に表現するために用いられる。ユニディフ・モデルunidiff modelやグッドマンのRC(Ⅱ)モデルも対数乗法モデルである。
対応分析correspondence analysisはセル数の多いクロス表の分布を記述するための分析法で,仮説検定のためではなく,探索的,記述的な分析に用いられる。林の数量化Ⅲ類と双対尺度法は対応分析とは独立に発展した分析法だが,対応分析と数学的には同じものであり,英語圏では対応分析という語が一般的になっている。多重対応分析はカテゴリー間の関係だけでなく,ケース間の関係も同時に分析する点で対応分析とは異なるが,カテゴリー間の関係については対応分析と似た結果が得られる。対応分析はクロス表の各カテゴリー間のカイ2乗距離を計算し,これを非類似性行列として固有値分解することで,多次元空間に非類似性行列をマッピングする。それゆえ計量多次元尺度法metric multidimensional scalingの一種とみなせる。カイ2乗距離chi-square distanceとは,クロス表におけるi行j列目のセル度数をnij,i行目の周辺度数をni・=Σjnij,j列の周辺度数をn・j=Σinijとすると,a行目とb行目のカテゴリーの間のカイ2乗距離は
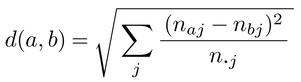
で定義される。列のカテゴリー同士のカイ2乗距離も同様に計算できる。
表5を対応分析で分析した結果が図である。
対応分析の結果は図のように示されることが多い。この図の見方は以下のとおりである。⑴周辺分布と類似した分布の行や列は,原点付近にプロットされる(C,乙)。逆に行や列の分布が周辺分布と異なるほど,原点から遠くにプロットされる(B,D,甲,丙)。⑵行のカテゴリーと列のカテゴリーが近くにプロットされる場合,両者は結びつきが強い(それらの行と列に対応するセル度数は,独立の場合の期待度数と異なる)。ただし,その結びつきの強さは,原点から離れているほど強い(Bと丙)。逆に原点付近で近くにプロットされていると,近くてもそれらの間に関連はほとんどない(Cと乙)。⑶行のカテゴリー同士,列のカテゴリー同士が近くにプロットされる場合,それらの行,列の分布は類似している(AとC,乙と丁)。⑷モデル全体の当てはまりの良さの指標として,軸ごとに固有値,正準相関係数(固有値の平方根),寄与率が計算される。二つの軸の寄与率の総和が1に近いほど,モデルと実際のクロス表の分布が近似している。行と列の関連の強さを知りたい場合は,正準相関係数を見る。これが大きいほど関連は強い。表5と図の例では,二つの軸の正準相関係数はそれぞれ0.32と0.11である。また分析に際しては,軸に名前をつけるなどして,軸/空間の性質を解釈する場合もある。対応分析は推定や検定をしないため,サンプルがどんなに少なくても分析できるし,カイ2乗距離を計算することに意味があれば,クロス表以外の行列型のデータを使うこともできる。多重クロス表であっても対応分析は可能である。
ロジスティック回帰分析logistic regression analysis(LRA),およびプロビット分析probit analysis(PA)は2値変数を被説明変数とした回帰分析で,被説明変数に二項分布を仮定し,それが1を取る確率(p)を予測する一般化線形モデルの一種である。LRAのリンク関数はロジット,ln
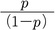 である。PAのリンク関数は正規分布の累積分布の逆関数である。両者の関数形は非常に似ていて,どちらを使っても実質的には同じ結果が得られることが多い。サンプル数が十分に大きいことを仮定したモデルであること,標準化係数や決定係数が計算できないことを除けば,どちらも通常の回帰分析と同じように分析・解釈できる。ただし,LRAの場合,k番目の共変量の係数bkは,共変量が1単位増加したときの
である。PAのリンク関数は正規分布の累積分布の逆関数である。両者の関数形は非常に似ていて,どちらを使っても実質的には同じ結果が得られることが多い。サンプル数が十分に大きいことを仮定したモデルであること,標準化係数や決定係数が計算できないことを除けば,どちらも通常の回帰分析と同じように分析・解釈できる。ただし,LRAの場合,k番目の共変量の係数bkは,共変量が1単位増加したときのln
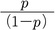 の変化量なので,そのままでは解釈しにくい。
の変化量なので,そのままでは解釈しにくい。そのため,exp(bk)や限界効果が計算されることも多い。exp(bk)は共変量Xkが1単位増加したときp/(1-p)が何倍になるかを示す。限界効果marginal effectとは,
pをXkで偏微分し,
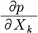 にX1,…,Xmの平均値を代
にX1,…,Xmの平均値を代入した値で,共変量がすべて平均値を取るときの,Xkのpに対する限界的な効果である。PAでも回帰係数はそのまま解釈することが難しいため,限界効果が計算されることもある。モデル全体の当てはまりの指標として,切片のみのモデルと比較したときの尤度比統計量や,逸脱度deviance(対数尤度×-2,-2LLとも表記される)が計算されることが多い。前者は大きいほど,後者は小さいほどモデルの当てはまりが良い。また,逸脱度を使った誤差減少率proportional reduction in error(PRE)を擬似決定係数quasi R2とよび,モデルの当てはまりの指標とする場合もある。さらに赤池情報量規準Akaike's information criterion(AIC)やベイズ情報量規準(BIC)がモデル選択の基準に用いられることもある。これらはいずれも小さいほど当てはまりが良い。 →回帰分析 →記述統計 →項目反応理論 →尺度 →多次元尺度法 →統計的推論
〔太郎丸 博〕
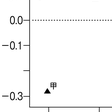
図 対応分析の結果

表1 性別と高リスク投資のクロス表

表2 表1に独立性を仮定した場合の期待…

表3 A 性別円B 職の有無円C 工員…

表4 階層的対数線形モデルを表3に当て…
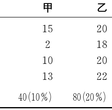
表5 架空の2元表
出典 最新 心理学事典最新 心理学事典について 情報

