最新 心理学事典 「統計的推論」の解説
とうけいてきすいろん
統計的推論
statistical inference
【統計的推論における基本概念】 統計的推論においては,実際に得られるデータは標本sampleとよばれる。標本は,研究において調べたい全要素からなる母集団populationから,その一部を抽出したものである。たとえば,有権者の内閣支持率の調査の場合,母集団は全有権者の内閣支持・不支持の意見であり,標本は実際に調査された有権者の内閣支持・不支持のデータである。統計的推論の方法を支える理論の根幹は,個々のデータに関して仮定される確率モデルprobabilistic modelである。たとえば,内閣支持率の調査の例であれば,標本に含まれる個々の有権者が支持を表明するか否かについて,「他の有権者とは独立に,母集団における支持率πに等しい確率で内閣を支持し,確率1-πで支持しない」という確率モデルを仮定する。このモデルを仮定することによって,標本における内閣支持率pが,どのような確率でどのような値を取るかを数学的に求めることができる。そうすると,標本における支持率pが母集団における支持率πの近傍(たとえばπ±0.01)に入る確率などを計算することができ,統計的推論のための基盤ができる。なお,今の例における標本支持率(より一般的には標本比率)pのように,標本データから計算によって求められる値を標本統計量sample statisticとよび,母集団支持率(より一般的には母集団比率)πのように母集団の特徴を表わす値を母数(パラメータ)parameterとよぶ。また,標本統計量がどのような確率でどのような値を取るかを示す分布を,その標本統計量の標本分布sampling distributionとよぶ。標本分布は,記述統計における実際のデータの散らばり状況を示す分布とは異なり,確率的にどのような値が得られやすくどのような値が得られにくいかを示す確率分布probability distributionである。
ところで,今の例における「他の有権者とは独立に,母集団における支持率πに等しい確率で内閣を支持し,確率1-πで支持しない」という確率モデルは,「母集団において内閣を支持する者の比率はπで,支持しない者の比率は1-πである」という母集団における分布の状況,すなわち母集団分布population distributionをそのまま反映したものとなっている。標本が母集団から無作為に抽出される場合には,母集団における支持率がπならば母集団から抽出される一つのデータが「支持」である確率もπとなるので,この確率モデルは自然かつ妥当なものである。このように,標本データに対して仮定される確率モデルの適切さは,母集団からの標本抽出samplingの方法に依存する。統計的推論において一般に前提とされる抽出法は,母集団からどの要素が選ばれる確率も等しく,また標本全体としてどの要素の組み合わせが選ばれる可能性も等しい抽出法である無作為抽出random samplingである。
【種々の確率モデルと標本分布】 変数が「支持-不支持」「賛成-反対」「正答-誤答」のように2値のときの確率モデル(および母集団分布)は,前記のように,2値のうちの一つが得られる確率(=母集団比率)πのみを含む単純なもので,ベルヌイ分布Bernoulli distributionとよばれる。このモデルのもとで,標本比率の標本分布は二項分布binomial distributionとよばれる分布となる。変数がテスト得点や反応時間などのように多値ないしは連続的な場合には,連続量の確率分布が確率モデル(および母集団分布)として仮定される。その代表的なものが正規分布normal distributionである。正規分布モデルのもとでの標本平均の標本分布は,同じく正規分布となる。変数間の相関関係を調べるときのように,各個人から二つの変数のデータが取られる場合は,二変数正規分布bivariate normal distributionのような二変数の同時分布が確率モデル(および母集団分布)として仮定される。二変数正規分布モデルのもとでの標本相関係数の標本分布は一般には非対称の分布となるが,標本相関係数にフィッシャーのz変換を施すと正規分布に近似することが知られており,この性質を利用して相関係数に関する統計的推論を行なうことができる。なお,フィッシャーのz変換以外の近似法もある。
【点推定と標準誤差】 統計的推論の一つの形式は,母数の値の推定estimationである。これには母数値を一つの値で推定する点推定point estimationと,母数値を含むと考えられる区間を算出する区間推定がある。区間推定については後述するとして,ここではまず,点推定について述べる。母数の点推定に用いられる統計量を推定量estimatorとよぶ。直観的には,母集団比率の推定には標本比率を用い,母集団平均の推定には標本平均を用いるなど,母数に対応する標本統計量を推定量とすることが考えられる。しかし,統計的推論においては,直観ではなく,なんらかの客観的な最適性の基準を設け,その基準を満たす統計量を推定量として選ぶアプローチが取られる。
推定量の最適性の代表的な基準の一つは,最大尤度基準maximum likelihood criterionであり,この基準を最適化する推定法は最尤法maximum likelihood methodとよばれる。尤度likelihoodとは,得られた標本データに対して,「母数の値がいくらなら,このような標本データが得られる確率はいくら」というように,その標本データが得られる確率を母数値の関数として表現したものである。最尤法は,たとえば標本比率が0.8となるデータは,母集団比率がいくらのときに最も得られやすいかを調べ,その確率(=尤度)を最大にする値を推定量とする方法である。最尤法によって得られる推定量を最尤推定量という。標本比率,標本平均,標本分散,標本相関係数は,それぞれの対応する母数の最尤推定量であることが知られている。
推定量の最適性の代表的な基準のもう一つは,最小2乗基準least squares criterionであり,この基準を最適化する推定法は最小2乗法least squares methodとよばれる。たとえば母集団平均の推定量として,標本における各データとの差異の2乗和(最小2乗基準)が最小になるものを選ぶとすると,その基準を満たす最小2乗推定量は標本平均であることが導かれる。最小2乗法は,二変数データにおける回帰直線の推定,さらには因子分析や構造方程式モデルにおける母数の推定においても利用されている。最小2乗法は確率モデルに依存しない方法であるため,適用可能な範囲が広いが,確率モデルを仮定しないままでは,推定量に関する確率論的な議論には限界がある。
推定量を選択する基準としては,このほかに,不偏性unbiasednessとよばれる基準がある。これは,標本ごとに値が変動する推定量の期待値が母数の値に一致するという基準であり,これを満たす推定量は不偏推定量unbiased estimatorとよばれる。たとえば標本比率と標本平均は不偏推定量であるが,標本分散と標本相関係数は不偏推定量ではない。ただし,標本分散にn/(n-1)を乗じて修正すると不偏推定量となり,不偏分散unbiased varianceとよばれる。なお,この場合のnは標本の大きさを表わす。
点推定を行なう際に重要なことは,推定量の値(推定値estimate)と母数値との差,すなわち誤差の大きさを査定することである。ただし,母数値が未知のため,推定値の誤差を直接求めることはできない。そこで,推定量が標本ごとにどの程度変動するかに注目し,推定量の標本分布の標準偏差を求める。この標準偏差は推定量の標準誤差standard errorとよばれる。たとえば標本比率の標準誤差が0.2だとしたら,この推定量は0≦p≦1の比率の範囲で0.2の大きさの標準偏差をもって変動するということであり,安定した正確な推定量とはいえないことがわかる。標本比率などの推定量の標準誤差は,標本の大きさの平方根に比例して小さくなることがわかっている。標準誤差の公式を参照することにより,「標準誤差をいくら以下に抑えるには,標本の大きさをいくら以上にすればよいか」という観点から標本の設計をすることができる。
【検定】 統計的推論のもう一つの形式は,母数の値に関する仮説の検定hypothesis testである。たとえば,「2群の母集団平均の差は0である」という仮説を立て,標本データによってその仮説が棄却できるかどうかの検定をする。そして,その仮説が棄却されたら,有意差significant differenceがあったと結論するという推論方式である。仮説が棄却されれば有意な結果と判断されるので,仮説の検定は有意性検定significance testともよばれる。ここで,「2群の母集団平均の差は0である」という仮説は,通常,棄却されるべく設定されるもので帰無仮説null hypothesisとよばれる。
帰無仮説が棄却されるか否かは,標本データから算出される検定統計量test statisticが,あらかじめ設定された棄却域に含まれるか否かによって決められる。今の2群の平均値差の検定の例では,2群の標本平均の差を,その標準誤差の推定量で割ったt統計量が検定統計量となる。2群のデータが,平均・分散ともに等しい正規分布から独立に得られたという仮定(確率モデル)のもとで,このt統計量はt分布とよばれる0を中心とした確率分布に従うことがわかっている。一般的に用いられる両側検定two-sided testでは,棄却域をその分布の両裾に設定する。一方の裾のみに設定する場合は片側検定one-sided testとなる。両側検定の場合は,0から十分に離れた両裾の値が,帰無仮説が真のときには得られにくく,逆に帰無仮説が偽のときには得られやすいからである。具体的にはある小さな確率αを定め,帰無仮説が真のときに検定統計量が棄却域に入る確率がαとなるように棄却域を両裾に設定する。このαは有意水準significance levelとよばれる。αは,帰無仮説が真であるときにそれを棄却する誤り(第1種の誤りtypeⅠerrorという)の確率であることから,危険率hazard ratioともよばれる。逆に帰無仮説が偽のときに帰無仮説を棄却しない誤りは第2種の誤りtypeⅡerrorとよばれる。これは,母集団では差があるのにそれを見逃して検出できなかったという誤りである。帰無仮説が偽のときに,第2種の誤りを犯さず,母集団での差を検出することのできる確率を検定力または検出力powerとよぶ。検定力の観点から必要な標本の大きさの検討を行なうことは検定力分析または検出力分析power analysisとよばれている。
検定の結果は,設定した有意水準に対して有意か否かを判断する方式のほか,どの有意水準のもとでぎりぎり有意になる結果かという観点から評価することもできる。得られた結果をぎりぎり有意にする有意水準はp値p-value,限界水準critical levelなどとよばれる。この指標は,標本データから計算される一種の統計量である。
上記の2群間の平均値差の検定は,1908年にゴセットGosset,W.S.(筆名はStudent)が導出した1群の平均に関する検定を,フィッシャー(1925)が2群の比較に拡張したものであり,ともにt検定t-testとよばれる。フィッシャーはその後,2群間のt検定を一般的な分散分析analysis of varianceに拡張し,さらに回帰係数に関する検定など多くの検定法を導出した。彼は最尤法の考案者でもあり,統計的推論全般に非常に大きな貢献をした統計学者である。ネイマンNeyman,J.とピアソンPearson,E.S.は,1928年の論文で検定における2種類の誤りを区別し,1933年には「所与の第1種の誤りの確率(有意水準)のもとで最小の第2種の誤りの確率(最大の検定力)を生じる検定」(最強力検定most powerful test)という明快な原理によって,検定統計量を定める重要な理論を発表した。ネイマンは後述する信頼区間に関しても大きな理論的貢献をしている。現在,仮説検定や有意性検定とよばれている理論や方法は,これらの先達によって20世紀初頭の比較的短い期間に基礎が形成されたものである。
正規分布を中心とする確率モデルを想定した検定法に対し,特定の分布形に関する仮定をおかない一連の検定法はノンパラメトリック検定non-parametric test(distribution-free testとも)とよばれ,1940年代からさまざまな検定法が提案されている。これとの対比で,正規分布モデルに基づくt検定や分散分析などはパラメトリック検定parametric testとよばれている。
【区間推定interval estimation】 母集団における平均値差や相関係数などの母数が0であるという帰無仮説が検定によって棄却されないとき,それは母数が0であることを意味しているわけではなく,母数が0のときにでも十分に得られるデータであるということ,すなわち0という母数値と整合的なデータであるということを意味している。この場合,0以外にも標本データと整合的な値は無数にある。言い換えれば,検定によって棄却されない母数値の区間があるということである。このような考え方に従って,たとえばα=0.05の両側検定で棄却されない母数値の区間を求めることができる。この区間は,標本ごとに変動するが,このようにして求められる区間が真の母数値を含む確率は1-α=0.95となることが示せる。95%の確率で真の母数値を含む区間という意味で,これを95%信頼区間confidence intervalとよぶ。このとき,確率1-αは信頼水準confidence levelとよばれる。信頼区間によって母数の推定をする方法は区間推定とよばれる。
信頼区間は標本のデータによって棄却されない母数値の集合であるから,その区間に0が含まれていれば,母数が0であるという帰無仮説は棄却されず,0が含まれていなければ,その帰無仮説は棄却されることになる。このように,信頼区間から検定の結果も知ることができる。さらに信頼区間は,その幅の狭さによって,推定の精度を示すことができる。信頼区間の幅が広ければ,標本データと整合的な母数値が広い範囲にわたることになり,明確な結論は導けないことになるが,幅が狭ければ,それだけ強い推論ができることになる。また,標準誤差と同様に,「信頼区間の幅をいくら以下に抑えるには,標本の大きさをいくら以上にすればよいか」という観点から標本の設計をすることができる。
検定の利用に関しては,「母数が0であるという帰無仮説を棄却しただけなのに,母数が実質的に意味のある大きさであるかのような解釈をしている」とか「有意な結果と有意でない結果の間に実質的に大きな違いがあるかのような解釈をしている」などの批判がなされることがある。信頼区間を利用または併用すれば,データと整合的な母数値の区間を直接的に示すことになるので,前者の解釈の誤りを避けることができ,また有意な結果と有意でない結果の間で信頼区間の重なりが大きければ,相互に矛盾しない結果であることもわかるので,後者の解釈の誤りを避けることもできる。信頼区間にこのような利点があることから,検定のみに依存せず,差の大きさや関連の強さの指標(効果量effect sizeと総称される)の値およびその信頼区間を報告し,合わせて解釈することが望ましいとされている。
【ベイズ法Bayesian approach】 統計的推論の方法としてここまで述べた点推定と標準誤差,検定,そして信頼区間による区間推定は,すべて共通の原理に基づいている。それは母数の値は未知ではあるが一つの固定した値であるということ,そして確率を考えるときはつねに母数の値を所与としたときのデータの確率のみを考えるということである。たとえば検定では,帰無仮説が真であるときの検定統計量の標本分布を基に棄却域を設定する。信頼区間についても,標本ごとに変動する区間が一つの母数値を含む確率を信頼水準とする。このように,母数を所与としたときのデータの確率はP(D|H)のように表現することができる。ここでPは確率,Dはデータ,Hは母数値ないしは母数値に関する仮説を表わし,かっこ内の縦線の後(H)を所与の条件として,縦線の前(D)に関する確率を問題にしていることを示す。
これに対し,ベイズ法では,P(H|D)の確率,すなわちデータが与えられたときに,母数値や仮説に関する確率を求めることを目的とする。この確率はデータが得られた後の確率という意味で事後確率posterior probability,またその分布は事後分布posterior distributionとよばれる。たとえば,母集団における2群間の平均値差に関する事後分布が得られれば,その差は95%の確率である特定の区間に含まれるという直接的な推論を行なうことができる。これも区間推定の一種であるが,前述の信頼区間が,母数そのものに関する確率ではなく,変動する区間が母数値を含む確率を問題にしていたのと対照的である。また,帰無仮説やその他の仮説についても,データに基づいてそれらの仮説が真である確率を直接求めることができる。このように,ベイズ法は,「データに基づいて母数や仮説についての推論をする」という統計的推論の目的に対し,自然で直接的な答えを提供する方法であるということができる。
ベイズ法において,母数や仮説に関係している事後確率P(H|D)が求められるのは,
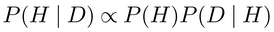
と表記されるベイズの定理Bayes' theoremをその根拠としている。この式の右辺のP(H)はデータが得られる前の母数や仮説に関する確率,すなわち事前確率prior probability(その分布は事前分布prior distribution)であり,P(D|H)は母数や仮説を所与としたときのデータの確率,すなわちデータが得られたときの母数や仮説の尤度である。この式は,事後分布が事前分布と尤度の積に比例することを示している。このうち尤度については,ベイズ法以外のアプローチでも用いられているものであるが,事前分布P(H)はベイズ法独自のものであり,ベイズ法の適用の是非に関する議論の焦点になるものである。
事前分布は,母数や仮説に関する事前の知識を基に設定されるが,そこには設定者の主観が入るため,だれにとっても同一の事前分布とはならない。したがって,データは同一であっても,最後に得られる事後分布は異なるものとなる。ベイズ法のこの性質は,分析者の事前知識を分析に反映させられる利点であると同時に,ベイズ法の広範な普及を妨げる要因でもあった。しかし,標本がある程度大きくなると,事前分布の違いに関係なく,事後分布は類似したものになってくる。そこで,事前分布に事前の知識を反映させることを差し控え,事前には知識がなかったものとして無知を示す中立的な事前分布を設定することによって,主観性の問題を回避することもできる。近年,事前分布へのこうした柔軟な立場と,数値計算アルゴリズムの発展によって,ベイズ法の適用が増えてきている。
【仮定からの逸脱と頑健性】 前述のように統計的推論は,個々のデータに関する確率モデルを前提とした理論および方法であり,実際のデータに適用する際には,どのような確率モデルが想定されているかを踏まえ,その適用可能性について判断する必要がある。現実には,たとえば離散的な評定値を用いる場合に連続的な正規分布を仮定するなど,確率モデルが厳密には成り立たないケースも多いが,実際上重要なのは,仮定した確率モデルが厳密に成り立つか否かではなく,仮定した確率モデルからの逸脱の度合いに対して,その確率モデルに基づく統計的推論がどの程度妥当な結果を与えてくれるかという頑健性robustnessである。各種の統計的推論の頑健性については研究の蓄積があり参考にすることができるし,コンピュータ・シミュレーションを利用して,個別の逸脱状況における頑健性を評価することも可能である。なお,仮定からの逸脱を問題にするとき,母集団分布の形や母集団分散の均質性などが注目されることが多いが,現実には母集団の定義そのものが曖昧なままデータが取られることも少なくない。また,母集団が明確に定義されている場合でも,そこからの無作為抽出という前提が満たされないことも多い。その場合,型どおりの統計的推論を適用した結果がどのような意味をもちうるかについてはさまざまな議論がなされている。 →記述統計 →ノンパラメトリック検定
〔南風原 朝和〕
出典 最新 心理学事典最新 心理学事典について 情報

