最新 心理学事典 「項目反応理論」の解説
こうもくはんのうりろん
項目反応理論
item response theory
各項目に対する反応が，潜在特性尺度latent trait scaleの値を既知とする条件付き確率を表現するモデルである。古典的テスト理論classical test theoryでは正答項目数で受験者の能力や特性の程度を表現していたのに対して，潜在特性尺度上に受験者を位置づけてその受験者の能力や特性の程度を表わす点に特徴がある。
項目反応理論は複数のモデルに対する総称で，いずれのモデルにおいても受験者はその能力や特性の程度に応じて潜在特性尺度上の一点に位置づけられ，複数のテスト項目に対する解答パターンから潜在特性尺度値が推定される。
従来の古典的テスト理論では取り扱えない問題に対して有効な解決法を与えてくれるため，心理テストに限らず，教育テスト，外国語テスト，医療系のQOL尺度開発などの場面で北米地域や欧州，オーストラリアなどではすでに実用水準で用いられていた。しかしわが国の公的試験などで用いられるようになったのは最近のことである。
【項目反応理論の特徴】 項目反応理論は，⑴項目の困難度が，受験者集団とは独立に潜在特性尺度上の一点として定義される。⑵受験者の特性尺度値（たとえば能力の）が，解答した項目群とは独立に潜在特性尺度上の一点として定義される。⑶項目の困難度と受験者の潜在特性尺度値とが同一の尺度上に位置づけて表わされる。⑷項目の特性は，特性尺度値と正答確率の関係を表わす後述の項目特性曲線に集約されて記述される。⑸ある項目に正答するか誤答するかは，他の項目に正答したか誤答したかの影響を受けず，相互に独立である（局所独立性local independence）。⑹測定精度が潜在特性尺度値の関数として表わされ，尺度値ごとにきめの細かい測定精度の評価が可能になる，という特徴をもつ。
【項目反応理論のモデル】 項目反応理論は，基本的には受験者の反応が正答か誤答かなどの2段階で表わされる場合に適用される2値型項目反応モデルと，受験者の反応が段階づけられた三つ以上のカテゴリーで表わされる場合に適用される多値型項目反応モデルに大別される。受験者の反応が名義的な複数のカテゴリーで表わされる場合や，連続型変数で表わされるモデルも理論的には存在するが，実用的な測定場面で用いられた例は現段階ではほとんど見られない。多くのテストでは受験者の解答（回答）を「正答-誤答」あるいは，「はい-いいえ」などの2段階で得るため，2値型反応モデルがよく用いられる。2値型反応モデルはさらに項目の特性を表わすパラメータ数に応じて，1パラメータ・ロジスティック・モデル，2パラメータ・ロジスティック・モデル，3パラメータ・ロジスティック・モデルに分けられるが，ここではまず2パラメータ・ロジスティック・モデルについて述べる。
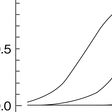
【項目特性曲線item characteristic curve】 項目反応理論では，テスト項目の特性はすべて項目特性曲線で記述される。この曲線は，受験者の潜在特性尺度値と受験者がその項目に正答する確率との関係を表わし，潜在特性尺度値の単調増加関数で表現される。具体的な曲線として，心理学で伝統的に用いられてきたロード（1952）の正規累積曲線normal ogive curveがあるが，現在は理論的な展開や実際的な取り扱いが容易な関数で表現されるロジスティック曲線logistic curveが用いられている。たとえば，2パラメータ・ロジスティック・モデルtwo-parameter logistic modelの場合は，潜在特性尺度値θと正答確率Ｐj（θ）との関係が，
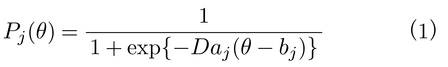
という関数で表わされる（図1）。ここで，添字ｊは項目番号を区別するために用いられ，Ｄは1.7が用いられることが多く，このとき正規累積モデルと同一の項目パラメタ値で項目特性曲線がほぼ完全に一致する。
ｂjは項目特性曲線の位置を決めるパラメータで，値の大きい方が，項目特性曲線が右寄りになり，同じ潜在特性尺度値θに対して正答確率が低くなり，当該項目の困難度が高いことを表わす。このためｂjは項目困難度item difficultyを表わし，困難度パラメータdifficulty parameterとよばれる。ここで項目困難度ｂjが，受験者の特性値θと同一の潜在特性尺度上で表現される点が特徴である。
また，ａjは項目特性曲線の立ち上がりの程度（勾配）を決めるパラメータで，値の大きい方が項目特性曲線の立ち上がりが急になり，ｂjの前後での正答確率の変化が大きく，特性尺度値間の違いを正答確率の差によく反映するという意味で項目識別力item discriminationが高いことを表わす。このためａjを識別力パラメータdiscrimination parameterとよぶ。
このモデルでは，困難度パラメータと識別力パラメータとで項目特性曲線が定められるため，2パラメータ・ロジスティック・モデルとよばれる。
【局所独立の仮定assumption of local independence】 複数項目から構成されるテストにおける受験者の正誤（回答）パターンに対して，項目反応理論では局所独立の仮定がおかれる。これは基本的かつ重要な仮定で，複数項目から構成されるテストに対する反応について，ある受験者を特定したとき「ある項目に対する反応は，ほかのどの項目に対する反応とも独立に生ずる」ことを仮定する。能力テストの場合でいうと，ある受験者が項目Ａに正答したか誤答したかが，項目Ｂに正答するか誤答するかにまったく影響しないという仮定である。この仮定は，項目Ａの結果を使って項目Ｂに解答するなど，項目間に特別な関係がある場合を除いて成立する仮定である。すなわち，潜在特性尺度値θを固定したときに項目応答パターン（ｕ1，ｕ2，…，ｕn）の生ずる確率Prob（ｕ1，ｕ2，…，ｕn｜θ）が，
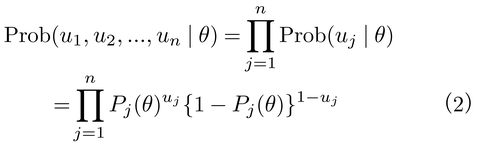
となることを仮定する。ここでｕjは項目ｊに対する受験者の反応を表わし，正答ならば1，誤答ならば0になる。
【テスト情報量amount of test information】 実際のテストでは解答結果から受験者の潜在特性尺度値を推定することが必要であるが，観測された受験者の正誤反応パターン（ｕ1，ｕ2，…，ｕn）からθの値を最尤法maximum likelihood methodにより推定することが多い。最尤法とは，θを未知の連続変数としたときに，実際に観測された項目反応パターンが得られる確率の変化を表わす関数（尤度関数）が最も大きくなるθの値をもって推定値とする方法である。この最尤法で得られた推定値θ＾は，
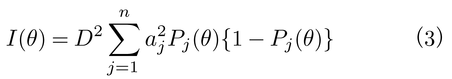
とすると，その標準誤差が
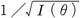で表わされるため，項目反応理論ではＩ（θ）をテスト情報量とよび，テストの精度を表わす指標として用いられる。Ｉ（θ）はθの関数であり，値が大きいほど精度が高いことを表わす。なお，⑶式の右辺は項目ごとに計算される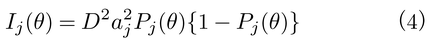
の和になっており，Ｉj（θ）を項目情報量amount of item informationとよぶ。
【項目反応理論と古典的テスト理論】 項目反応理論は，古典的テスト理論と比べて以下に示す点に特徴がある。
⑴個人の測定結果を潜在特性尺度上の値で表わし，古典的テスト理論のテスト得点（正答数得点）が厳密には順序尺度の水準であるのに対して，モデルの上では間隔尺度として構成されるため，統計的分析を加えるのにより妥当なデータが得られる。⑵各項目の特性が項目特性曲線のパラメータで表わされるため，古典的テスト理論の通過率および点双列相関係数のように指標の値を求める集団に依存することがなく，受験者集団によらず項目パラメータの不変性invariance of item parametersが成り立つ。⑶テストの測定精度をテスト情報量で表わすため，異なる特性尺度値をもつ個人ごとにそのテストによる測定精度を評価することができる。古典的テスト理論の信頼性係数の場合は，テスト全体としての精度を表わすため，いわばそのテストの受験者に対する平均的な精度を示し，特定の個人についてそのテストで良い測定が実施されたかどうかは評価できなかった。⑷適応型テストのように解答する項目が受験者間で異なる場合でも，同一特性尺度上の値で測定結果を表示することが可能であるが，古典的テスト理論では，正答数得点で測定結果を表わすため，異なる項目に解答した受験者間の測定結果を相互に比較することは不可能であった。⑸テストを構成する項目の一部を新しいものと入れ替えても，特性尺度値を基にテストの解釈規準を設定するため，テストの標準化をやり直す必要がないが，古典的テスト理論の場合には，項目を入れ替えると基本的には標準化の手続きをやり直す必要が生ずる。標準化を実施するにはかなりの労力を要するため，このことがテスト項目の更新が円滑に進まない理由の一つになっていたが，項目反応理論の場合はテスト項目の更新と標準化の手続きとが分離されているため，つねに最新の項目を用いてテストを構成できる。
以上の特徴により，項目反応理論は実際のテスト開発場面で強力な道具を提供している。
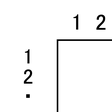
【項目パラメータ値の推定】 ここまではテスト項目のパラメータ値を既知として説明を進めてきたが，実際のテストではまず各項目のパラメータ値（ａj，ｂj）を推定する必要がある。基本的には受験者Ｎ名分の項目反応パターンを観測した大きさＮ（名）×ｎ（項目）の項目反応行列をデータとして（図2），そのようなデータが得られる確率の変化を表わす関数（尤度関数）が最も大きくなる（ａj，ｂj），ｊ＝1，…，ｎの値をもって推定値とする。各受験者の潜在特性尺度値θを推定する場合と異なり，多変数関数の最大値を求めることになるために複雑な数値計算が必要になる。実際の推定法には同時最尤推定法，周辺最尤推定法，ベイズ推定法などがある。
【多肢選択形式を念頭においたモデル】 実際のテストでは多肢選択形式が用いられることが多い。この場合，当て推量random guessingにより正答することができるため，潜在特性尺度値θに対してその分正答確率が上昇する。これをパラメータとして組み込んだものが3パラメータ・ロジスティック・モデルthree-parameter logistic modelである。項目特性曲線は，
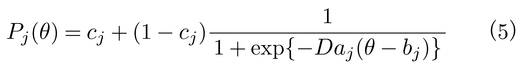
で表わされ，ｃjが当て推量による正答確率の増加分に関係するパラメータである。
【ラッシュ・モデルRasch model】 識別力がすべての項目で等しく困難度のみ項目間で異なることを仮定するモデルで，1パラメータ・ロジスティック・モデルone-parameter logistic modelともよばれるが，モデルの成立に関してデンマークの数学者ラッシュRasch,G.が別の文脈から導出したという経緯を尊重して，とくにラッシュ・モデルとよばれることが多い。項目特性曲線は，
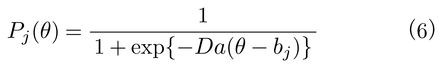
で表わされ，ｂjのみがパラメータになる。
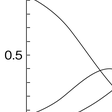
【多値型項目反応モデル】 観測変量が多値型の場合を扱うモデルで，多値型の反応が段階（順序）づけられたカテゴリーで与えられる場合に用いられる段階反応モデルgraded response model，一般化部分得点モデルgeneralized partial credit model，名義的なカテゴリーで与えられている場合に用いられる名義反応モデルnominal response modelなど複数のモデルがある。多値型項目反応モデルでは，各項目のカテゴリーごとに潜在特性尺度値と当該カテゴリーに反応する確率との関係を表わす項目反応カテゴリー特性曲線item response category characteristic curve（IRCCC）が設定される（図3）。
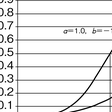
段階反応モデルの場合，まず潜在特性尺度値と当該カテゴリー以上の値をもつカテゴリーに反応する確率との関係を表わす境界特性曲線boundary characteristic curve（BCC）を設定し，それにロジスティック曲線
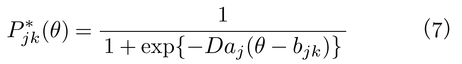
を用いる（図4）。ただし，添字ｊは項目，ｋはカテゴリーを表わす。すなわち，2値型の場合の2パラメータ・ロジスティック・モデルを拡張したものである。そして，隣接するカテゴリー間のBCCの差が各カテゴリーに受験者が反応する確率を表わし，項目反応カテゴリー特性曲線になる。
一般化部分得点モデルの場合，項目反応カテゴリー特性曲線は，
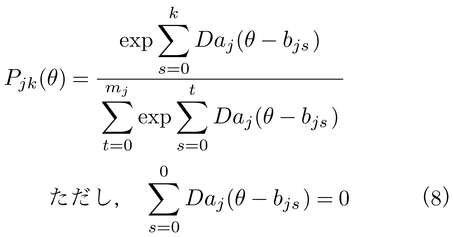
で表わされ，ラッシュ・モデルを多値型に拡張し，さらに項目間で識別力の違いを許したものである。
名義反応モデルの場合，項目反応カテゴリー特性曲線は，
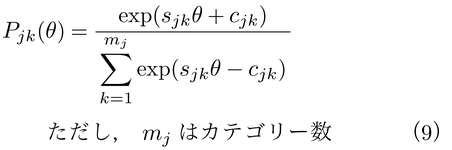
で表わされるが，パラメータは項目反応カテゴリー特性曲線の形状を決定するだけで，内容的な意味づけはできない。
【項目反応理論の適用場面】 項目反応理論は単一のテスト・データを分析するだけでなく，テストの実際的な問題を解決するのに有用である。
まず等化equatingである。たとえば，複数の時期で実施され，時期間で問題項目の異なるテストの場合に，難易度が完全に同一ではない異なる時期間の得点を比較するには，異なる時期のテストによる測定結果を共通尺度上の得点で表示できるようにする必要がある。この操作を等化という。TOEFLなど有力な外国語能力試験では，等化が実施されているため受験時期によらず受験者にとって公平な測定が実現されている。
次に特異項目機能differential item functioning（DIF）の検出であるが，これは測定すべき能力が同一水準であるにもかかわらず，属する集団が異なる受験者間で同一項目の困難度が異なるという現象が特定の項目で観測されることをいう。項目の困難度は属する集団に関係なく，同一の能力水準にある受験者に対して等しくなければ，テストの公平性が保てない。元来はテストの公平性を検討するために利用されたが，最近は異文化間比較研究などで質問項目の翻訳等価性に加えて，社会文化的文脈での意味的な等価性を検討するのに積極的に利用されている。
適応型テストadaptive testとは，当該受験者を測定するのに最適な項目を，すでに整備された項目プール中から逐次的に選択して実施する手順を繰り返すテスト方式のことをいう。基本的には「直前に実施した項目に対して受験者が正答した場合には，次にはより難しい項目を提示し，逆に受験者が誤答した場合には，次にはよりやさしい項目を提示する」という手続きを逐次繰り返す。一般的には，各項目の出題ごとに，それぞれの受験者の特性を，最もよく識別する項目を選択して出題する方法である。実施した項目セットが異なるにもかかわらず，測定結果が相互に比較可能である。実用水準ではTOEFL-CBTで用いられていたが，現在はTOEFL-iBTに改定されて適応型テスト方式は用いられなくなっている。
【項目反応理論に関する注意点】 項目反応理論には前述のモデル以外のモデルも提案され，また利用されている。項目反応理論は強力なテスト理論であり，実用的にも優れた特徴をもつが，すべての測定場面やテストに対して適用できるわけではない。たとえば，「局所独立の仮定」が成り立たない問題構成になっているなど，モデルの仮定が満たされないテストや，受験者数の少ないテストに対して適用しても意味がない。たとえば，教師が作成したクラスルーム・テストや外国語学習に際して最初のクラス分けに利用されるプレイスメント・テストなどのように，限定された集団に対して特別な目的をもって実施されるようなテストなどでは，必ずしも項目反応理論を適用する必要はなく，古典的テスト理論の枠組みで十分有用な情報が得られる。また，項目反応理論でも複雑なモデルが単純なモデルよりも優れていて説明力が大きいとは限らない。モデルは「活用する」ことが大切で，「濫用」に陥っては，むしろテストの質を低くしてしまうということに注意が必要である。 →古典的テスト理論 →信頼性 →妥当性
〔野口 裕之〕
出典 最新 心理学事典最新 心理学事典について 情報