最新 心理学事典 「記述統計」の解説
きじゅつとうけい
記述統計
descriptive statistics
【グラフによる表現】 得られたデータがどのような尺度であるかによって適切なグラフが異なる。データが名義尺度である場合，棒グラフや円グラフが適切である。たとえば，ある集団の職業の分布を表わす場合である。データが離散的な数値や順序で与えられる場合も，棒グラフや円グラフなどが使われる。データが連続的な場合，それぞれの値を取る観測対象（ユニット）の数を数えるのは現実的ではない。そのようなときには，連続的な値をいくつかの区間に分け，その区間に属する対象の数を数えて，その頻度を棒や点で表わすことができる。目盛り付きの棒グラフともいうべきグラフをヒストグラムhistogramという。数値を点で表わし，点の間を線で結ぶグラフを折れ線グラフという。折れ線グラフは，軸をデータの取得時期に取り，時間による変化（成長など）を示す場合にも使われる。二つ以上の変数の間の関連を図示するグラフは，散布図scatter diagramとよばれる。二つの変数をｘとｙとするとき，ｘ軸にｘの値，ｙ軸にｙの値を取り，その交点をプロットする。平面（ｘとｙ）の上に点が散らばっているように見えるので散布図とよぶ。
【中心的傾向の測度】 一つの変数について，いくつかの観測値が得られる。この1群のデータのもつ情報を，一つの数値に要約するには，その代表的な値，すなわち中心的傾向を示すことになる。中心的傾向を示す値としてよく使われるのは，平均mean，メディアンmedian（中心値ともよぶ），モードmodeである。平均は，総和をデータの数で割った値である。メディアンは，1群のデータを順序に並べ替え，前から数えても後ろから数えても同じになる順位のデータを指す。たとえば，5人の身長をデータとするとき前から数えて3番目，後ろから数えても3番目の順位の身長がメディアンである。ただし，観測値の数が奇数の場合には，このような順位の者が存在するが，偶数の場合には存在しないので次のように定義する。
ｎ個のデータが得られたとする。すなわちｘ1，ｘ2，…，ｘnである。これを，小さい値から順位を付けたものを，ｘ(1)，ｘ(2)，…，ｘ(n)と表わす。まず，観測値の数が奇数の場合，すなわちｎ＝2m＋1の場合は，メディアンはｘ(m+1)である。偶数の場合，すなわち，ｎ＝2mで表わされる場合は，メディアンはｘ(m)とｘ(m+1)の平均である。モードは最も頻度が高い値である。連続な値を取るデータでは，頻度を問題とすることが妥当ではない場合がある。観測値の値を区間に分け，最も多く頻度が観測される区間の中間値をモードとする。ヒストグラム上では，最も高い棒（または点）をもつ区間の中央値である。
【ばらつきの測度】 データのもつ情報を要約する場合に，中心的傾向の要約値の次に重要なのがばらつきvariabilityの測度である。ばらつきの測度として，分散variance，標準偏差standard deviation（分散の平方根），範囲range，四分位偏差quartile deviationなどがある。分散は分布の広がりの程度を表わす。ｎ個のデータｘ1，ｘ2，…，ｘnの分散ｓ2は
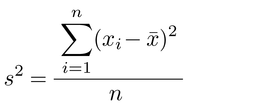
である。分散として，ｎではなく，（ｎ－1）で割ることを推奨されることがある。区別するときには，前者を標本分散，後者を不偏分散とよぶ。標準偏差は分散の平方根である。範囲はデータの最大値と最小値の差で，四分位偏差は75％値と25％値の差である。そのほかに，データの分布がどの程度歪んでいるか，あるいはどの程度尖っているかの測度として，それぞれ歪度や尖度がある。
【多変量データの記述】 二つの変数のデータを記述する場合，それぞれの変数の中心的傾向やばらつきの測度を報告するだけではなく，二つの変数の間の関連の度合いが重要な情報である。変数間の関連の度合いの測度は，一般に相関係数とよばれる。相関係数にはいろいろな種類があり，たとえばそれぞれの変数が連続の場合（間隔尺度や比尺度の場合）はピアソンの積率相関係数，それぞれが順序尺度の場合にはスピアマンSpearman,C.E.やケンドールKendall,M.G.による順位相関係数が用いられる。また，それぞれが名義尺度の場合には，関連の指標は，独立を仮定した場合の分布からどの程度離れているかによって定義される関連指数が用いられる。
三つ以上の変数間の相関係数は，相関係数行列にまとめられるが，大きな相関係数行列から一見して全体的なパターンを見つけることは困難なことが多い。たとえば，
10の変数に対して，
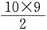＝45個，50個の変数に対して1225個の相関係数が得られる。このような膨大な数の相関係数から直接その構造を見いだそうとするのは難しく，相関係数行列の構造を表現する方法が必要とされた。その代表が，ピアソンの積率相関係数行列（または共分散行列）を分析する主成分分析principal component analysisである。なお，数値的には似た結果を算出するが，因子分析factor analysisは統計モデルに基づく推論による結果を示すものであり，データの記述をする方法とはいえない。
変数間の関係が，変数間の隔たりを示す距離によって表現されている場合，その構造を示す方法が多次元尺度法multidimensional scalingである。ただし，多次元尺度法が対象とする距離は，厳密に定義される数学的距離ではなく，隔たりの心理的順位づけを示す順位尺度程度の測度も距離という。したがって，類似度を適当に変換すれば，距離とみなされるので，多次元尺度法は距離や類似度の変数間行列から，構造を見いだそうとする方法であると一般化することができる。数学的な距離行列を対象とする場合（より正確にいえば，数学的な距離にデータを変換できる場合）を計量多次元尺度法，数学的とはいえず距離を示す順位尺度を分析する場合を非計量多次元尺度法とよぶ。観測対象に対する属性の記述がカテゴリーとして与えられる場合，すなわち観測値が名義尺度の場合に，カテゴリーや各個体に，適切な数値を与える方法がさまざまな名称でよばれている。すなわち林式数量化理論Ⅲ類，多重対応分析，双対尺度法，等質性分析である。これらの分析方法は，個体に与える数値とカテゴリーに対し，データが発生させるメカニズムを考慮し，それを最もよく表現するように数値を与える方法である。 →因子分析 →尺度 →主成分分析 →相関係数 →多次元尺度法
〔繁桝 算男〕
出典 最新 心理学事典最新 心理学事典について 情報