多次元尺度法（読み）タジゲンシャクドホウ（英語表記）multidimensional scaling

デジタル大辞泉

たじげんしゃくど‐ほう〔‐ハフ〕【多次元尺度法】

⇒多次元尺度構成法

出典　小学館

最新 心理学事典

たじげんしゃくどほう
多次元尺度法
multidimensional scaling

MDSと略称される。対象間の距離的データを分析して，近接する対象同士は近くに，隔たる対象同士は遠くに位置づけられる空間布置を求める手法であり，多次元尺度構成法multidimensional scalingともよばれる。距離的データとは，人同士の心理的隔たりや知覚される刺激間の非類似性など，数学的に定義される距離そのものではないが，距離で近似される数値を一般に指す。

【多次元尺度法の基礎】　ｎ個の対象同士の距離的データからなるn×nの正方行列Ｑの要素をｑ^ij（対象ｉとｊの距離的データ）と表わそう。ここで，ｑ^ij＝ｑ^jiである。さらに，MDSの解として得られるｎ対象×ｐ次元の座標行列Ｘの要素をｘ^ir（対象ｉの次元ｒの座標値）と表わそう。座標値から定義されるｉ，ｊ間のユークリッド距離Euclidean distance



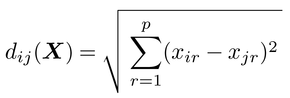
に誤差が加わったものが，データｑ^ijであるとみなす。これがMDSの基本モデルである。ｑ^ijが比尺度上の数とみなせる場合には，誤差平方和



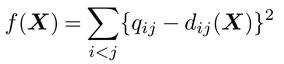
を最小化する座標行列Ｘが求める解となり，Ｘに基づいて対象の空間布置を描ける。なお，解Ｘに右から直交行列Ｔを乗じたXTも解であり，得られた布置は直交回転できる。

【計算のアルゴリズム】　多次元尺度法で用いる計算のアルゴリズムalgorithmについて説明する。前述の最小化には反復解法を要する。解法の一つは，Ｘに関するｆ（Ｘ）の偏微分に基づく最適化法を用いるものであるが，距離ｄ^ij（Ｘ）の定義に平方根が現われるため，偏微分が1/ｄ^ij（Ｘ）の関数となり，もし反復途中にｄ^ij（Ｘ）＝0が発生すれば計算不可能になる。この危惧を伴わない解法が，1970年代後半から1990年代にかけて，デ・レーウde Leeuw,J.，ハイザーHeiser,W.J.やフローネンGroenen,P.J.F.などのオランダの計量心理学者を中心に開発された優関数法majorization algorithmである。この方法の基本は，Ｘと同じサイズの行列をＺで表わすと，次の3条件を満たす関数ｇ（X,Z）を用いることにある。 ⑴平方根が現われず，Ｘに関する最小化が容易である。⑵ｇ（X,Z）≧ｆ（Ｘ）。⑶ｆ（Ｚ）＝ｇ（Z,Z）。固定されたＺに対してｇ（X,Z）を最小化するＸをＸ^*と表わすと，⑵と⑶より



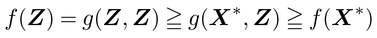
が得られ，上記の最小化のたびごとにｆ（Ｘ）が減少することがわかる。以上の解法は，MDSのアルゴリズムPROXSCALで用いられる。

　平方根が現われないようにｆ（Ｘ）を変形したアルゴリズムが，1970年代中ごろに高根芳雄らによって開発されたALSCALであり，データと距離の平方に基づく



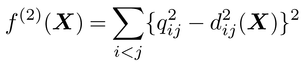
を最小化する。さらに時代をさかのぼると，トーガソンTorgerson,W.S.（1952）とガウアーGower,J.C.（1966）が独立に主座標分析principal coordinate analysisとよばれる方法を開発している。これは，ｄ^2ij（Ｘ）からなるｎ対象×ｎ対象の行列Ｄの左右から，ｎ次の単位行列Ｉとｎ×1の1＝［1,1,…，1］′に基づく行列Ｊ＝Ｉ－ｎ^-111′を乗じると－0.5JDJ＝JXX′Ｊになることに着目し，データも同様に変換して定義される∥－0.5JQJ－JXX′Ｊ∥²を最小2乗基準とする方法であり，反復計算を要しない，

　さて，ｑ^ijが間隔尺度上の数とみなされる場合には，切片ｃを加えた基準



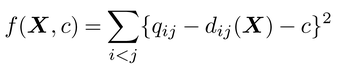
を最小にするＸ，ｃを求めればよい。ｑ^ijを順序データとみなすMDSはとくに非計量多次元尺度法nonmetric multidimensional scalingとよばれ，



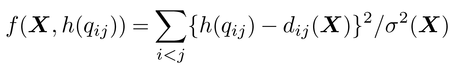
を最小化する。ここで，σ²（Ｘ）は距離ｄ^ij（Ｘ）のｉ，ｊを通した2乗和または分散であり，これを分母にする目的は，すべての点が同一点になるといった退化した解の回避である。またｈ（ｑ^ij）は，ｑ^ij＜ｑ^klならばｈ（ｑ^ij）≦ｈ（ｑ^kl）を満たす関数であり，Ｘを固定したうえでｆ（Ｘ，ｈ（ｑ^ij））を最小にするｈ（ｑ^ij）は，クラスカルKruskal,J.B.（1964）の単調回帰法によって求められる。

【多次元展開法multidimensional unfolding】　行と列を異なる対象が占めるｎ個体×ｍ変数のデータ行列Ｚに対するMDSを，とくに多次元展開法とよぶ。ｎ個体×ｐ次元の座標行列をＸ，ｍ変数×ｐ次元の座標行列をＹ，各行列の要素をそれぞれｘ^ir，ｙ^jrで表わすと，個体ｉと変数ｊの距離は



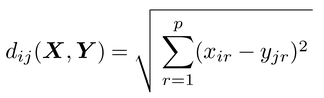
と表わせ，Ｚの要素ｚ^ijとの誤差平方和



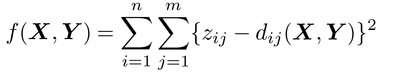
を最小にするＸ，Ｙが，多次元展開法によって求められる。これを，たとえば参加者ｉが刺激ｊを好むほど小さい値を取るデータｚ^ijに適用すると，各刺激とそれを好む参加者どうしが近くに，嫌う参加者が遠くに位置づけられる空間布置が得られる。

【個体差多次元尺度法individual difference scaling（個体差MDS）】　再び，ｎ個の対象同士の距離的データの正方行列Ｑに着目し，それが複数個ある場合，つまりデータがn×nの行列Ｑ^k（ｋ＝1，…，Ｋ）で表わせるケースを考えよう。たとえば，Ｋ人の参加者がｎ個の対象間の非類似性を評定した場合，Ｑ^kは参加者ｋの対象ｉ，ｊに関する評定値ｑ^ijkから成る。参加者間の個体差を考慮しながら上記のデータを分析するための拡張型MDSが，1970年前後のホランHoran,C.B.やキャロルCarroll,J.D.らの考案に始まる個体差多次元尺度法であり，次の二つの仮定に基づく。⑴すべての個体（参加者）に共通する対象の座標行列Ｘ（その要素はｘ^ir）が存在する。⑵個体ｋにとっての対象ｉ，ｊ間の距離的データは，重みつきユークリッド距離weighted Euclidean distance



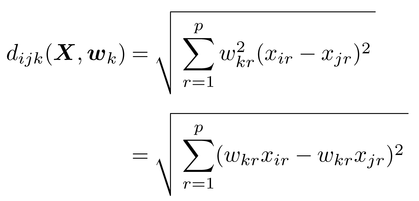
によって近似される。ここで，ｗ^kの要素ｗ^2krは参加者ｋが次元ｒに与える重みを表わし，個体差を説明する役割を果たす。以上の仮定のもとに，個体差MDSでは，



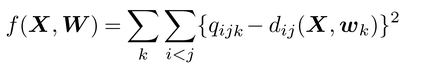
を最小にする座標行列Ｘと重みＷ＝［ｗ¹，…，ｗ^K］を求める。Ｑ^kのｋが時期や条件のようにヒト以外であっても，もちろん個体差MDSを適用できる。個体差MDSの特徴は，一般に座標行列Ｘを回転できないことにある。個体差MDSにも間隔・順序尺度のｑ^ijに対応できる方法があり，これらが実行できるようにするため，前述のアルゴリズムPROXSCALやALSCALは拡張されている。

　なお，最小2乗法だけでなく，最尤法やベイズ法に基づくMDSも開発されている。また，1970年代中ごろより，ｑ^ij≠ｑ^jiである非対称な距離的データに対するMDSの諸モデルも提案されている。　→多変量解析
〔足立 浩平〕

出典　最新 心理学事典

ブリタニカ国際大百科事典 小項目事典

多次元尺度法
たじげんしゃくどほう
method of multidimensional scaling

多次元尺度構成法ともいう。対象のもつ心理学的特性が単一の次元にそったものでなく，複雑な，多次元にそったものであると考えられる場合，それに一定の尺度値を与えるための手続きをさす。まず，当該の対象を含む一群の対象間の類似の程度を判断し，その結果に基づいて，それらの対象群にとって必要不可欠な心理的尺度を決め，それに応じて，一群の対象の尺度値が決定される。

出典　ブリタニカ国際大百科事典 小項目事典

ブランド用語集

多次元尺度法

多次元尺度法とは、データ間の類似度に関する情報が与えられたとき、データの位置関係を再現する手法のことをいう。

出典　(株)トライベック・ブランド戦略研究所