ポアソン分布（読み）ポアソンブンプ（その他表記）Poisson distribution

デジタル大辞泉

ポアソン‐ぶんぷ【ポアソン分布】

確率分布の一。xを負でない整数、eを自然対数の底として、λ^xe^x/x!で表される分布を、平均値λのポアソン分布といい、その標準偏差もλになる。一定期間における事故の発生や放射性物質の崩壊など、まれに起こる離散的な事象の頻度がこの分布で近似される。フランスの数学者ポアソンが導出。

出典　小学館

改訂新版　世界大百科事典

ポアソン分布 (ポアソンぶんぷ)
Poisson distribution

0および自然数全体のうえに分布している離散型確率分布の典型的な例である。正定数λをとり，kには確率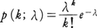，を置いたとき，分布p（k;λ）（k≧0）をポアソン分布という。この分布では平均値も分散もともにλである。また著しい特徴として，ガウス分布と同様にその再生性があげられる。X₁，X₂を互いに独立で，それぞれ平均値λ₁，λ₂をもつポアソン分布に従う確率変数とすれば，和X₁＋X₂の分布もポアソン分布p（k;λ₁＋λ₂）（k≧0）である。

　成功する確率がpの試行をn回独立に試みて得られる二項分布b（k;n，p）（0≦k≦n）も，nが大きくてpが小さく，np＝λがふつうの大きさのときはポアソン分布で近似される。すなわち，kがあまり大きくないときb（k;n，p）≈p（k;λ）。さらに，ポアソン分布があらわれる具体例としては，一定時間内の電話のコールや交通事故，放射性物質の崩壊などがある。いずれも時間帯を重なり合わない小時間区間に分けたとき，各区間での現象の生起が独立になるような場合である。
執筆者：飛田 武幸

出典　株式会社平凡社「改訂新版　世界大百科事典」

日本大百科全書(ニッポニカ)

ポアソン分布
ぽあそんぶんぷ
Poisson distribution

λ＞0として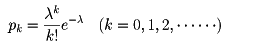

と置けば、p_k＞0,p₀+p₁+p₂+……=1であるから、｛p_k｝は確率分布（離散型）である。この確率分布をポアソン分布といい、P(λ)で表す。一定期間における事故の発生件数、放射性物質から一定時間内に放射される粒子の数、その他ポアソン分布で表される多くの例がある。まれにおこる現象の生起回数の分布がポアソン分布で近似されることは、次のように説明される。すなわち、確率pの事象がn回の繰り返しのうちにちょうどk回おこる確率p_kは
　　p_k=_nC_kp^k(1-p)^n-k　(k=0,1,……,n)
で与えられるが、もしpが小さく、nが大きく、λ=npが大きくも小さくもないとすると、前記のp_kに対して次の近似式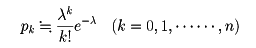

が成り立つのである。

　ポアソン分布P(λ)を折れ線グラフで表すと次のようになる。λが整数であれば、p_kはk＜λ-1のとき単調増加で、k=λ-1,k=λのとき最大値をとり、k＞λで単調減少である。λが整数でなければp_kは
　　k＜［λ］=（λの整数部分）
で単調増加で、k=［λ］で最大値をとり、k＞［λ］で単調に減少する。ポアソン分布P(λ)の平均値はλ、分散もλに等しい。母関数はe^λ(t-1)であり、特性関数はexp(λ(e^it-1))である。

［古屋　茂］

出典　小学館　日本大百科全書(ニッポニカ)

百科事典マイペディア

ポアソン分布【ポアソンぶんぷ】

x＝０，１，２，…などの値が出現する確率がe(−μ/)μ(x/)/x！で与えられる分布。平均値はμ，標準偏差は（式１）。工程が安定しているときの一定の大きさのサンプル中の欠点数，多人数中にまれに起こる偶発的社会現象（自殺，交通事故等）などがこの分布に従う。
→関連項目正規分布｜t分布｜ポアソン

出典　株式会社平凡社

ブリタニカ国際大百科事典 小項目事典

ポアソン分布
ポアソンぶんぷ
Poisson's distribution

確率密度分布の一つで，交通事故のように1人あたりとしてはきわめてまれな現象 (非常に確率の小さい偶然現象) を，比較的広い範囲で長い時間にわたって観測するときみられる分布。確率変数 X が離散型で，そのとる値が 0，1，2，3，… であって，Pr(X)＝e^-λ・λ^k/k!　(X＝k＝0，1，2，…)
であるとき，確率変数 X の分布をいう。この分布の平均値 m と標準偏差 σ はそれぞれ，m＝λ ，σ＝√λ となる。

出典　ブリタニカ国際大百科事典 小項目事典

世界大百科事典（旧版）内のポアソン分布の言及

【確率分布】より

…これは成功する確率がpであるn回のベルヌーイ試行における成功する回数の分布である。(2)ポアソン分布　Xは0,1,2，……の値をとり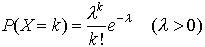，のとき，この分布がポアソン分布である。実例としては，電話のコールの回数とか放射性物質の崩壊など一定時間区間内に起こる回数の分布がある。…

※「ポアソン分布」について言及している用語解説の一部を掲載しています。

出典｜株式会社平凡社「世界大百科事典（旧版）」