サイクロイド（英語表記）cycloid

デジタル大辞泉

サイクロイド（cycloid）

円が一直線上または曲線上を滑ることなく転がるとき、この円の円周上に固定された一点が描く曲線。円が他の円の外周を転がるときにできる曲線をエピサイクロイド（外がいサイクロイド）、内側に接して転がるときにできる曲線をハイポサイクロイド（内ないサイクロイド）という。

出典　小学館

精選版 日本国語大辞典

サイクロイド

1. 〘 名詞 〙 ( [英語] cycloid ) 一直線上を一つの円がすべることなくころがるとき、この円の周上に固定された一点が描く曲線。また、円が直線ではなく他の円周の外側をころがるときできる曲線をエピサイクロイド（外サイクロイド）、内側をころがるときできる曲線をハイポサイクロイド（内サイクロイド）という。擺線(はいせん)。

出典　精選版 日本国語大辞典

ブリタニカ国際大百科事典 小項目事典

サイクロイド
cycloid

擺線 (はいせん) ともいう。半径 a の円が一直線 ( x 軸) 上を滑らないで転がるときの，円周上の1点 P の軌跡で，媒介変数表示による曲線の方程式は，x＝a(θ－ sin θ) ，y＝a(1－ cos θ) である。サイクロイドの名は，G.ガリレイによって命名され (1599頃) ，その後 C.ホイヘンスや J.ベルヌーイらによって研究された。もし，点 P が転円の中心から h(h≠a) の距離にあれば，Pの軌跡の方程式は，x＝aθ－h sin θ ，y＝a－h cos θ となる。この曲線をトロコイド trochoidという。ここで h＝a の場合がサイクロイドである。半径 a の円が，半径 b の固定円の周の外側あるいは内側を，周に沿って滑らずに転がって動くとき，この転円の周上の1点Pの描く軌跡は，それぞれ

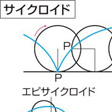
で与えられる。以上の曲線の方程式は，固定円の中心を原点とする直交座標系に関するもので，(1) を外サイクロイド (エピサイクロイドまたは外擺線) ，(2) を内サイクロイド (ハイポサイクロイドまたは内擺線) という。特に a＝b のとき外サイクロイドは心臓形となり，2a＝b のとき内サイクロイドは固定円の直径になる。点Pが転円と同一平面上にあるが，その周上にないとき，この点Pの軌跡を外トロコイド epitrochoid，内トロコイド hypotrochoidという。

出典　ブリタニカ国際大百科事典 小項目事典

日本大百科全書(ニッポニカ)

サイクロイド
さいくろいど
cycloid

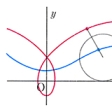
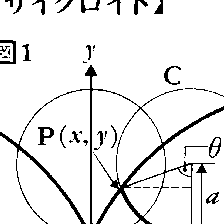
平面曲線の一つ。直線上を円が滑ることなく転がるとき、円上に固定された点の描く曲線であって、媒介変数を用いて、
　　x＝a(t－sint), y＝a(1－cost)
で表示される。道路を走る車の車輪の周上の1点の軌跡は、サイクロイドである。周の内側に固定した点や、外側に固定した点の軌跡をトロコイドtrochoidという。

　空間内に2点A、Bがあるとする。重力だけの作用を受ける質点がAからBまで動くとき、所用時間が最小になるのは、AとBを結ぶ直線に沿って動く場合ではなく、AとBをサイクロイドで結ぶ曲線に沿って動く場合である。このため、サイクロイドは最速降下線ともよばれる。

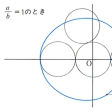
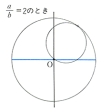
　円Oの外側を、他の円Cがこれに接しながら、滑ることなく転がるとき、この円C上に固定された1点の軌跡を、エピサイクロイドepicycloidという。動円Cが、円Oに内接しながら転がるときの動円C上の固定された点の軌跡を、ハイポサイクロイドhypocycloidという。円Oの半径aと円Cの半径bの比が、簡単な整数比の場合に、きれいな曲線ができる。エピサイクロイドでa/b＝1のときカージオイド（心臓形）、ハイポサイクロイドでa/b＝2のとき線分、a/b＝3のとき尖点(せんてん)三つの曲線、a/b＝4のときアステロイド（星芒形(せいぼうけい)）となる。

［竹之内脩］

[参照項目] | 変分法

サイクロイド（円上に固定された点の軌跡…

サイクロイド（トロコイド）

サイクロイド（エピサイクロイド）

サイクロイド（アステロイド）

出典　小学館　日本大百科全書(ニッポニカ)

改訂新版　世界大百科事典

サイクロイド
cycloid

平面上で，円Cが直線lに接しながら，その上を滑らずに転がるとき，円Cの周上の点Pの描く図形Γをサイクロイドまたははい（擺）線といい，lをその底線という。円Cの半径をaとするとき，その方程式は，Cの回転角θを媒介変数として，x＝a（θ－sinθ），y＝a（1－cosθ）で与えられる（図1）。サイクロイドΓを図2のように下向きにおくとき，一様な重力の場の下では，質点がΓ上の任意の点PからΓに沿って滑りもっとも低い点Mに達するまでの時間は，摩擦がなければ，点Pの位置に関係せず一定である。この性質によりサイクロイドは等時曲線とも呼ばれる。また，点Aをそれより低いところにある点Bに結ぶ空間曲線に沿って，質点が摩擦をうけることなく重力の作用により滑り落ちるという運動を考えるとき，降下に要する時間が最小となるような曲線は，ABを含む鉛直面内でAを通る水平線を底線とするサイクロイドである（図2）。この性質により，サイクロイドは最速降下線とも呼ばれる。
執筆者：中岡 稔

図1～図2

出典　株式会社平凡社「改訂新版　世界大百科事典」

百科事典マイペディア

サイクロイド

擺線(はいせん)とも。一直線上を一つの円がすべらずにころがるとき，円周上の一定点がえがく軌跡。一つの円がもう一つの円の外（内）側を円周に沿ってすべらずにころがるとき，ころがる円の円周上の一定点がえがく軌跡をエピ（ハイポ）サイクロイドまたは外（内）擺線という。サイクロイド歯車に使われる曲線はエピサイクロイド。→トロコイド
→関連項目等時性｜歯車｜ピン歯車

出典　株式会社平凡社

世界大百科事典（旧版）内のサイクロイドの言及

【曲線】より

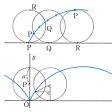
…(6)定曲線Cに接しながら，その上を他の曲線Γがすべらないでころがるとき，Γに対し固定された点Pの描く曲線をルーレットrouletteまたは輪転曲線といい，Cを底線，Γを転曲線，Pを極という。底線が直線で，転曲線が円周であるルーレットは，極が転曲線上にあるときにはサイクロイドcycloidまたは擺（はい）線，そうでないときにはトロコイドtrochoidと呼ばれる(図13，図14)。転曲線である円の半径をa，その中心から極までの距離をbとすれば，トロコイドは回転角tを媒介変数として，x＝at－b sin t,y＝a－b cos tと表される。…

【曲線】より

…(6)定曲線Cに接しながら，その上を他の曲線Γがすべらないでころがるとき，Γに対し固定された点Pの描く曲線をルーレットrouletteまたは輪転曲線といい，Cを底線，Γを転曲線，Pを極という。底線が直線で，転曲線が円周であるルーレットは，極が転曲線上にあるときにはサイクロイドcycloidまたは擺（はい）線，そうでないときにはトロコイドtrochoidと呼ばれる(図13，図14)。転曲線である円の半径をa，その中心から極までの距離をbとすれば，トロコイドは回転角tを媒介変数として，x＝at－b sin t,y＝a－b cos tと表される。…

【歯車】より

…　もっとも多く用いられている歯形曲線はインボリュート曲線である。またサイクロイド曲線や特殊歯形として他の曲線も用いられているが，いずれの場合においても，ピッチ点Pの位置が回転角速度比ω₁/ω₂をきめる決定的要素になっている。(1)インボリュート歯形　一般に用いられている平歯車およびはすば歯車(形は平歯車と似ているが，歯筋が軸に対して傾斜している)の歯形曲線はほとんどの場合インボリュート曲線であり，このような歯車をインボリュート歯車という。…

※「サイクロイド」について言及している用語解説の一部を掲載しています。

出典｜株式会社平凡社「世界大百科事典（旧版）」