歯車（読み）ハグルマ（英語表記）gear

デジタル大辞泉

は‐ぐるま【歯車】

１ 円柱・円錐台などの周縁に歯を刻んだもので、対にして歯をかみ合わせることにより、回転運動を確実に伝える装置。機械に広く用いられ、平ひら歯車・斜歯はすば歯車・傘かさ歯車・ねじ歯車・ウオーム歯車などがある。「歯車がかみ合う」
２ ある組織を動かしている仕組み。また、その要員。「管理社会の歯車に組み込まれる」
[補説]書名別項。→歯車

はぐるま【歯車】［書名］

芥川竜之介の短編小説。昭和2年（1927）遺稿として発表。激しい強迫観念にとらわれた知識人の絶望と狂気を描く。

出典　小学館

精選版 日本国語大辞典

は‐ぐるま【歯車】

1. [ 1 ] 〘 名詞 〙
   1. ① 回転する平板・錐体などの周囲に一定の大きさの歯をきざんだ機械の部品。小さなもので大きな力を確実に伝達することができる。平歯車・かさ歯車・はすば歯車・ねじ歯車などに分けられる。〔物理学術語和英仏独対訳字書（1888）〕
   2. ② 個人の力ではとうてい変えようのない社会の大きな流れを、動き続ける機械装置の①にたとえたもの。
      1. [初出の実例]「あらゆる悲劇や喜劇があちらでもこちらでも行はれてゐたのであったが、大きな歯車はそれ等のどれをも平然と運びながら」(出典：金（1926）〈宮嶋資夫〉八)
   3. ③ 大きな組織の一員として、ひたすら決められた通りに動かざるをえない立場の人を、大きな装置を構成する多くの部品のうちの一つとしての①にたとえたもの。
      1. [初出の実例]「実業家や役人になって、社会の歯車に組み入れられることを拒否したのである」(出典：夏目漱石論（1960）〈荒正人〉)
2. [ 2 ] 小説。芥川龍之介作。昭和二年（一九二七）遺稿として発表。錯乱と苦悩の中で激しい強迫観念におそわれ続ける「僕」（作者）の自己告白の記。

出典　精選版 日本国語大辞典

改訂新版　世界大百科事典

歯車 (はぐるま)
gear

ギヤともいう。2軸の間に回転を伝えたり，動力を伝える機械部品の一種。この種の運動を実現させるもっとも簡単な方法は，2軸にそれぞれ円筒を取り付けて，これを互いに押しつけながら摩擦力で回転させるものである。しかしこの場合，伝達動力が大きくなると，円筒どうしが互いに滑るようになり，動力の伝達が有効に行えなくなる。そこで両方の円筒の周辺に等間隔に突起をつけ，その一つ一つがかみ合うようにすると，滑りを起こさずに目的を達することができる。このようにしてできたのが歯車である。

　歯車は，ねじ，軸受などとならんで，もっとも多く用いられている機械要素の一つである。小型，中型のものは時計の歯車からクレーン，産業機械，化学装置などに用いられ，大型のものとしては舶用減速機の歯車をあげることができる。

発達の歴史

歯車の歴史は古く，アルキメデスも研究を行ったといわれ，またヘロンは歯車による連動装置をもった距離測定器についての記述を残している。時代が下ってルネサンス期になると，レオナルド・ダ・ビンチが歯車仕掛けの考案を多数ノートに残しているが，歯車が真に機械要素としての地位を確立するようになったのもこのころからといえよう。歯車の歯の形は昔はあまり問題にされず，ただ回転運動さえ伝えればよいとされていたのであるが，正確な運動を伝えることが要求されるようになってくると，幾何学的に正確な歯形をもつ歯車が必要になってきた。さらに産業革命の前後からしだいに学問的に扱われ，幾何学的解析も行われるようになり，なかでも，デンマークのO.レーメルやフランスの数学者カミュÉtienne Louis Camus（1699-1768）らの歯形の研究は有名である。現在の歯車の主流である，歯形にインボリュート曲線を用いるインボリュート歯車の価値が広く認識されるようになったのは19世紀の半ばころからで，そして歯を切る方法としての創成歯切り法が実用化（1877ころ）されると，これにもっとも適したインボリュート歯車が，一般工業分野において不動の地位を占めるようになった。

　歯車はこのような歴史的変遷を経て今日に至ってきたが，最近ではとくに歯車の負荷特性を高めるために，精度の高い歯車を作る技術，歯面（金属）の表面の強さを増大させるための窒化などをはじめとする特殊な表面処理，歯面損傷を防止するための歯車用潤滑油の開発が進んできている。このほか，騒音の少ない歯車を実現するための努力も行われているが，これについては現在なお未解決の問題が多い。

歯車のかみ合い原理

歯車には多くの種類があり，そのかみ合いも本来別々に論ずべきものであるが，ここではもっとも基本になる平歯車についてのみ論ずる。平歯車というのは，円筒の表面に軸と平行な歯筋をもつものであって，歯車の種類のところの図（図6-a）に示したように，一般の人が歯車といったときに思い浮かべるものである。

　現在使用されている歯車の大部分は，等速回転運動を伝えるためのものであるので，ここでも，この等速回転運動を伝達する歯車のかみ合いの原理を述べる。1対のかみ合っている平歯車は，幾何学的には1組の互いに接している円筒におきかえられる。すなわち1対の平歯車に回転運動を行わせるとき，それとまったく等価な純ころがり運動をする二つの円筒の接触におきかえることができる。この二つの円筒の断面の円を1対の平歯車のピッチ円という。

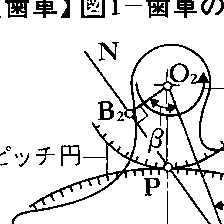
　いま，歯車のかみ合っている1組の歯を単純化して，図1のような回転する運動片（1）と（2）の接触におきかえて考える。運動片（1）と（2）が点Cで接触し，それぞれO₁，O₂を中心にω₁，ω₂の角速度で回転しているとする。共通垂線NNとO₁O₂交点をPとする。いま運動片（1）と（2）が互いにくいこまず離れないとすると，図1より，

　V₁cosα＝V₂cosβ　……（1）　

でなければならない。ここにV₁，V₂はそれぞれ運動片（1），（2）の点Cにおける速度であり，α，βはそれぞれV₁，V₂が共通垂線NNとなす角である。O₁，O₂からNNにおろした垂線の足をそれぞれB₁，B₂とする。そしてこれらの運動片の回転速度比をi（＝ω₁/ω₂）とする。このときV₁＝ω₁・O₁C，V₂＝ω₂・O₂Cであるから，これを前の（1）式に代入して，ω₁・O₁C・cosα＝ω₂・O₂C・cosβとなる。図1からわかるようにO₁C・cosα＝O₁B₁，O₂C・cosβ＝O₂B₂であるから，O₁B₁・ω₁＝O₂B₂・ω₂，したがって，i＝ω₁/ω₂＝O₂B₂/O₁B₁＝O₂P/O₁Pの関係が得られる。このことから，角速度比i＝ω₁/ω₂は，共通垂線NNが両運動片の回転の中心を結ぶ直線O₁O₂と交わる点Pから，それぞれの回転の中心O₁，O₂までの距離の比によってきまることがわかる。そしてこのiはふつうの歯車においては一定でなければならないから，点Pは定点となる。この点Pをピッチ点といい，O₁，O₂を中心として，点Pを通る円が先に説明したピッチ円である。

　ここにO₁P・ω₁＝O₂P・ω₂が成立するので，運動片（1）と（2）の点Pにおける周速度は等しく，点Pにおいては運動片（1）と（2）は滑りを伴わずに，純ころがり接触を行うことになる。換言すれば，図1における運動片（1）と（2）の接触運動は，二つのピッチ円どうしの純ころがり接触におきかえることができる。これが一般に歯形の機構学的必要条件と呼ばれているものである。

歯形曲線

ピッチ点Pが定点であるような曲線を運動片（1）と（2）にあたえると，これが歯車の歯形曲線となり，歯車としての機能を発揮することがわかる。この条件を満足する曲線の種類は無数にあるが，このうちで実用になる曲線，すなわち製作しやすいこと，多少の誤差があっても正確にかみ合うなどの条件を満たすのは，ごく限られたものとなる。

　もっとも多く用いられている歯形曲線はインボリュート曲線である。またサイクロイド曲線や特殊歯形として他の曲線も用いられているが，いずれの場合においても，ピッチ点Pの位置が回転角速度比ω₁/ω₂をきめる決定的要素になっている。

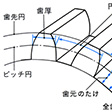
（1）インボリュート歯形　一般に用いられている平歯車およびはすば歯車（形は平歯車と似ているが，歯筋が軸に対して傾斜している）の歯形曲線はほとんどの場合インボリュート曲線であり，このような歯車をインボリュート歯車という。インボリュート曲線は，一つの円（基礎円という）に糸をまきつけ，この糸を，緊張した状態でほどいていったとき，その糸上に固定された1点が描く曲線である（図2）。歯形曲線としてインボリュート曲線が重要視される理由としては，この種の歯車は製作が容易なので安価であること，精度が高いこと，取付誤差が多少あっても（軸間距離が多少あっても）正確なかみ合いをすることおよび1種類の工具で種々の歯形を製作することが可能であることなどがあげられる。図3にインボリュート平歯車の例を示し，この図の中で歯車に関する基本的な用語を説明しておいた。なお，ピッチ円の直径（単位mm）を歯数で除したものをモジュール（モデュールともいう。記号m）というが，これは歯の大きさを表す一つの尺度でもあり，この値が大きいほど歯も大きい。また，歯の大きさを表すものとして，インチ制の歯車では，歯数をピッチ円の直径（インチ）で割ったダイヤメトラルピッチ（記号P）が用いられる。

（2）サイクロイド歯形　歯形曲線としてインボリュート曲線の次に多く用いられている曲線がサイクロイド曲線である。歯形に用いられるサイクロイド曲線は，図4に示したように，円Oに外接および内接してころがる，ころがり円上の1点a，cが描く曲線であって（前者を外転サイクロイド，後者を内転サイクロイドという），これら二つの曲線が点bでつながる形になっている。実際に歯面に用いられるのは外転サイクロイドと内転サイクロイドの一部である。歯形曲線にサイクロイドを用いた歯車をサイクロイド歯車といい，インボリュート歯車より歯の干渉が少ないという利点はあるものの，製作が容易でなく，時計，計器などの限られた分野以外にはほとんど用いられていない。

（3）ノビコフ歯車　上記のインボリュート歯車，サイクロイド歯車のほかに，なおいくつかの特殊歯車がある。その代表的な歯車としてあげられるのがノビコフ歯車である。この歯車は，はすば歯車の一種で，平歯車としては成立しない。この歯形と，かみ合いの状態を図5に示したが，歯形は小歯車の歯形が凸の円弧，大歯車の歯形が凹の円弧になっている。ただし，実際のノビコフ歯車はこの凸の円弧と凹の円弧が完全に一致するようには作られていない。接触歯面応力が小さく，滑りもないので大きな負荷能力をもち得るという利点があり，日本でも，一部においてこのノビコフ歯車を基本にしての技術開発が行われており，実際に用いられている。

歯車の種類

（1）平歯車spur gear　平歯車はもっとも多く用いられているもので，図6-aに示されているように，円筒面上に歯筋が軸と平行になっており，平行な2軸間の伝動に用いられる。円筒面上に歯筋を設ける代りに，円筒の内面に歯筋を設けたものが内歯車である（図6-b）。また平歯車の直径を無限大にしたものがラックrackで（図6-c），小歯車（この場合ピニオンpinionと呼ばれる）と組み合わせることによって直線運動と回転運動との間の変換を行うことができる。なお，インボリュート曲線は直径を無限大にすると直線になるので，インボリュート歯車ではラックの歯形は直線歯形となる。

（2）はすば歯車helical gear　図6-dに示されているように，歯筋が軸に対して傾斜している歯車で，平行な2軸間の伝動に用いられる。高速回転に適するが，回転を伝えるときに軸方向の推力を発生する欠点がある。この推力を打ち消すために2個のはすば歯車を組み合わせて歯筋のねじれが左右対称になるようにしたものにダブルヘリカルギヤ（図6-e），やまば歯車（図6-f）がある。

（3）かさ歯車bevel gear　相交わる軸（ふつうは軸角90°）の間に使われる歯車で，円錐面上に歯をもつ。歯筋の形で分類すると，直線状の歯筋が円錐の頂点に向かっているすぐばかさ歯車，歯筋は直線であるが，円錐の頂点には向かわずに傾斜しているはすばかさ歯車および歯筋が曲線状の曲がりばかさ歯車（スパイラルベベルともいう）となる。また，かさ歯車の内端部から外端部へいくに従って，歯の高さが変わらないものと変わるものとがあり，前者を等高歯，後者をこう配歯という。

（4）ハイポイドギヤhypoid gear　交差せずに，食い違っている2軸（ふつう軸角90°）の間の伝動に用いられる歯車で，かさ歯車に似た形状をもつ。ふつうの曲がりばかさ歯車に比べて，取付けが強固にできること，小歯車のねじれ角を大きくすることにより軸の径を大きくすることが可能で強度を増大できること，減速比がかさ歯車より高くとれること，騒音が低いなどの利点がある。歯筋の形（大歯車におけるもの）は種々あり，円弧，インボリュート，トロコイドなどが用いられている。

（5）ウォームギヤworm gear　食違い軸間に用いられる歯車の一種。図6-iのようにねじ状の歯筋をもつウォームと，これとかみ合うウォームホイールよりなり，動力は必ずウォームからウォームホイールのほうへ伝達される。一般の歯車の減速比は1：10程度までであるが，ウォームギヤでは1：10から1：100くらいまでの間の減速比が容易に得られる。歯のかみ合い率を増大させ，負荷特性をよくするものとしてウォームの形状を鼓のような形にした鼓形ウォームギヤ（グロボイドウォームギヤ）があるが，製作，使用がむずかしく，効率も下がる傾向がある。ウォームにはふつうは焼入れ鋼を用い，表面を研削して仕上げ，ウォームホイールにはリン青銅または鋳鉄などが用いられる。

（6）ねじ歯車screw gear　二つのはすば歯車からなるが，軸が食い違った状態にあるところに用いられるものをいう。製作が容易であること，ねじれ角，軸角，軸間距離，減速比を適当に選ぶことができるうえに，組立誤差があってもかみ合いを正確に保てるなどの利点をもっているので，実用的である。しかし歯面間のかみ合いは点で行われ，滑り速度が高く摩耗が激しいので，主として運動伝達か軽荷重動力伝達用として用いられている。

（7）特殊歯車　ここでは変則的な相対運動をする歯車の一例として，偏心歯車と非円系の歯車，ゼネバ歯車，間欠歯車について述べる。偏心歯車は，同形，同大のインボリュート歯車2個を，図6-kに示すようにそれぞれ回転の中心を同じ量だけ偏心させて組み合わせたもので，歯車O₁を等速回転運動させた場合でも，他方は周期的な不等速回転運動を行う。非円系歯車には，図6のlとmに示した，オーバル歯車，楕円歯車などがある。両方とも楕円形をしている歯車であるが，回転中心の位置が異なっている。両者とも，駆動歯車O₁を等速回転運動させても，従動歯車O₂は等速回転運動はせずに，周期的な不等速運動を行う。ゼネバ歯車と間欠歯車は間欠運動を実現させるためのもので，前者は割出し機構に多用されている。図6-nにゼネバ歯車の一例として四つの溝をもったものを示したが，駆動車のピンと従動車の溝がかみ合い，駆動車は連続運動をし，従動車は間欠的に回転することになる。間欠歯車は図6-oに示したような歯車装置で，駆動車には円周上の一部にしか歯切りされていない。従動車は，ほとんど全円周にわたって歯切りされているが，一部に歯切りされていない部分があり，これが駆動車の歯切りされていない部分と接する。駆動車の連続運転によって従動車は間欠運動するが，この間欠運動は駆動車の歯切りされている部分が全体の何分の1になっているかによってきまる。

歯車の歯数

平歯車の歯数は少なくなるほど製作がむずかしくなり，歯車の性能（負荷特性）が低下する。歯数が少なくなると，滑り速度が高くなり，また，滑り率も極度に高くなり，歯面は潤滑に関して非常に不利な状態におかれることになる。このため一般には，極端に少ない歯数は実際には使われない。円筒歯車（平歯車，かさ歯車など，円筒をピッチ面とする歯車）において，最小歯数は何枚であるかについて，簡単に記しておくと，インボリュート平歯車の場合は，1組の歯車で歯数が等しい場合は最小歯数は5枚である。サイクロイド歯車では3枚が最小歯数である。はすば歯車の場合は歯がねじれているので，歯数はさらに少なくすることができ，極端な場合は歯数1枚の歯車を作ることも可能となる。実際用いられている円筒歯車の歯数はふつうは12枚以上で，できれば16枚以上が望ましい。この範囲にある歯車は製作するときも，使うときにも，無理のない状態にあるからである。

歯車の工作法

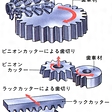
歯車の工作法は切削による方法と非切削による方法に大別される。切削による方法にも多くの方式があるが，もっとも多く用いられている方法は，創成歯切り法と呼ばれ，ラックカッターあるいはホブを用いて歯形を切り出すものである。インボリュート平歯車において，これと幾何学的に正確にかみ合うラックを考える。いま，ラックの歯を切刃とし，これに図7-aのように被切削歯車を同じ位置にもってきて，それぞれに図のような運動を与えれば，ラックとかみ合うインボリュート平歯車を創成することができる。このような工具をラックカッターといい，さらに，より能率的にこの創成歯切りを行わせるようにしたのがホブで，ラックカッターの各刃に似た刃をねじ筋に沿って配置してある。かさ歯車の創成では，ラックカッターに代わるものとして冠歯車（かさ歯車のピッチ円錐が平面になったもの）が用いられる。冠歯車の歯形が直線であるときは，これにより創成される歯形は球面インボリュートではなく，オクトイド歯形となるが，オクトイド歯形は実際上は球面インボリュートに非常に似ており，かつ厳密な球面インボリュートの歯車は製作が困難なため，実際には近似的にこのオクトイド歯形を球面インボリュートとして扱う。

　創成歯切り法以外の，比較的多く用いられている方法として，金属粉末を高温で焼結させて作る方法があり，最近この方面の技術が進歩し量産に用いられている。また歯の全歯たけをもつ転造工具を利用して，塑性加工により，押しながら回転して作り出す方法，さらに特殊加工法として，金型を用いて鍛造により作り出す方法などもある。
→歯切盤

転位

前述したようにインボリュート歯車は現在もっとも多く用いられているが，その理由の一つとして，転位という方法を採用することによって同一の工具で種々の歯形を切り出せることがあげられる。ふつうのインボリュート歯車の歯切りは，図8-aのように，ラックカッターの中心線（基準ピッチ線）が切削されるべき歯車のピッチ円に接するようにして行われ，このようにして作られる歯車は標準歯車と呼ばれる。これに対して図8-bのようにラックカッターの位置を被切削歯車の半径方向に動かし（これを転位という），ラックカッターの中心線からある距離だけ離れた一つの直線をピッチ線として，被切削歯車のピッチ円をこのピッチ線に接するようにして歯切りしたものを転位歯車という。ラックカッターのピッチ線がラックの中心線より下に移行するときの歯切りの状態を正転位，この反対の場合を負転位という。正転位では，一般に歯元は太くなり，歯は折損に対して強くなるが，負転位を行った場合は一般に歯元は狭くなり，歯は折損に対して弱くなる。ただし正転位を極端に大きく行うと歯先のとがりを生じるので，実際の歯車では，わずかに正転位させて歯切りをしたものが多い。このような転位を行うことによって歯の折損に対して強い歯車を作れる（正転位による）のみならず，軸間距離をある範囲内で自由にとることができるなどの利点が得られる。

歯面の表面仕上げ

精度の高い歯車を得るための歯の表面を仕上げる方法としてシェービング仕上げ，ラッピング仕上げ，研削仕上げなどが行われる。シェービング仕上げは焼入れ前の軟らかい歯面に対して行われるもので，歯面に多数の細い溝をもつ歯車またはラックを工具とし（これをシェービングカッターという），その歯を被工作物（歯車）の歯溝に入れ，ねじ歯車のようなかみ合い運動を行わせて歯面を仕上げる。この操作は精度はあまり上がらないが，歯面の凹凸がとれ，偏心などを取り去るのに有効で，加工の能率（速度）がよく量産に適している。

　ラッピング仕上げは歯切り後熱処理をしたときに生じたわずかの誤差を取り除いて歯車の精度を高め，また歯面に生じたスケールなどを取り除いて歯面を滑らかに仕上げるために行う仕上げ法の一つである。仕上げられる1組の歯車，あるいは仕上げられる歯車とラップ歯車と呼ばれる鋳鉄製の歯車をかみ合わせ，ラッピング剤を歯面につけて回転させて仕上げるが，あまり長くしすぎると，歯形誤差を生じ，かえって性能を落とすこともある。量産する歯車の仕上げにはあまり採用されないが，ハイポイドギヤおよびかさ歯車などのような複雑な形状のものには採用されている。

　研削仕上げは歯面をといしで研削することにより仕上げる方法で，歯溝の形に仕上げた成形といしを用いて歯面を研削する方法と，インボリュート歯形の創成と同じ原理に基づく創成研削の二つの方法があるが，現在では後者の方式が広く採用されている。創成研削にもいろいろの方式があるが，代表的なものは，ねじ状のといしを用いる方式，2枚のさら形といしを用いる方式，1枚のラック状といしを用いる方式などである。

歯形修正とクラウニング

幾何学的に正しいインボリュート歯形と正しいピッチをもつ歯車は，正しい回転運動を伝えることができる。しかし実際の歯車は弾性体（ほとんどの場合金属）で作られているため，荷重が加わると歯が変形し，正確な運動が伝わらなくなる。さらに歯車の製作誤差や取付誤差などがあれば，現象はいっそう複雑になる。このようなときに，かみ合いの誤差の原因になる種々の要因を取り除く方法として歯形修正やクラウニングをほどこすことが行われる。歯形修正とは，歯先か歯元のすみ肉部に近い位置において，歯をけずり落とすことをいうが，もっとも多く行われるのは歯先修正である。また，例えば平歯車において，歯車の組立てのときの誤差，あるいは荷重による軸のかたよりなどのため，かみ合う歯車どうしの2軸が平行にならない場合，両歯車の歯筋が一致せず，歯幅の端で接触する（片当り）ようになりやすい。これを防止して，過大な接触圧力を発生しないようにするために歯筋にふくらみをもたせることが行われる。このような歯筋の修正をクラウニングといい，かさ歯車やハイポイドギヤにおいても行われる。
執筆者：成瀬 長太郎

図1～図8

出典　株式会社平凡社「改訂新版　世界大百科事典」

日本大百科全書(ニッポニカ)

歯車
はぐるま

円筒や円錐面に設けた多くの歯が次々にかみ合いながら運動を伝達する機械要素。2本またはそれ以上の軸の間に回転や動力を伝えるのに使用される。ギヤ（ギア）gearともいう。1個の歯車だけでなく、組になったものを歯車とよぶこともある。歯車のように、歯が円周上に配列されている機械要素としては、スプロケット（鎖車(くさりぐるま)）、ラチェットなどがあるが、かみ合う相手が、同じような歯面をもたないチェーンや爪なので、一般的には歯車とはよばない。動力を伝達する機械装置には歯車のほかにベルト、チェーン、リンク装置、摩擦伝動装置などがあるが、歯車は小形で確実に運動を伝達し、寿命も長く、大きな動力を伝達でき、効率もよいので機械装置に広く利用されている。動力を伝えるもっとも簡単な方法は、2軸に円板を取り付けその外周を互いに接触させればよい。しかしこのような方法では、回転数が増加した場合や、接触圧力が小さい場合には、円板の周囲で滑りがおこり確実な伝達ができなくなる。そこで両方の車の外周に等間隔に突起をつくり、それらを互いにかみ合うようにすると、回転数が多くなっても滑りをおこさず、大きな動力の伝達もできる。このようにしてできたものが歯車である。

　歯車にはその形、大きさなどきわめて多くの種類がある。小さいものは時計用の直径1.5ミリメートル程度のものから、大きなものは船舶用の減速装置などに使用されている直径数メートルに及ぶものまであり、工作機械、車両をはじめ、あらゆる種類の機械に利用されている。

［中山秀太郎・清水伸二］

歴史

歯車の歴史は古く、紀元前からつくられ利用されていた。アルキメデスやヘロンらも歯車を利用して各種装置をつくった。水時計などにも運動を伝えるための大小の歯車が使用されていた。紀元前につくられ、1000年以上も利用された水車にも、その運動を伝えるための歯車が使われた。最初のころは、円板の周囲に丸棒を等間隔に植えて使用した。17世紀ころには、水車を動力とした製粉所や鍛造所、製材所などがしだいに増え、歯車を使っての動力の伝達が各所で行われるようになると、性能のよい歯車を製作する必要性が高まった。また時計の製作も本格的になったので歯車についての科学的研究が始まった。円板の周辺につける歯形の形についての研究、また歯車の組合せについての研究などがしだいに盛んとなり、摩擦損失の少ない高性能の歯車がつくられるようになった。

　歯車の歯の形には、サイクロイド曲線を使用したサイクロイド歯形と、円に巻き付けた糸を引っ張った状態でほどいていくとき糸の先が描く軌跡であるインボリュート曲線を使用したインボリュート歯形とがある。歯車の使用が増えるにつれて、歯形に関する研究が多くの学者によって行われた。最初のころはサイクロイド歯形をもつ歯車と、円板にピンを植えたピン歯車とについての研究が行われたが、18世紀になって数学者レオンハルト・オイラーはインボリュート歯車についての研究を始めた。19世紀の中ごろになって創成歯切り法が実用化したあとは、多くの歯車にインボリュート歯形が用いられるようになった。サイクロイド歯形は摩耗が少なく、回転が非常に滑らかであるなどの長所をもっているが、工作がめんどうであるため、時計などの精密機械、あるいは計測器類の歯車に用いられているにすぎない。これに対し、インボリュート歯形は工作が容易であることをはじめ多くの長所のために一般に広く用いられ始め、19世紀なかばすぎからは歯車の大部分を占めるようになった。

　歯車の歯と歯がかみ合っている接触点から中心までの距離を半径とする円をピッチ円という。ピッチ円上で隣り合う歯形の対応する同じ点間の距離を円ピッチという。そのほか歯車の歯の各部にはいろいろな名前がつけられている。

［中山秀太郎］

歯車の種類

回転運動を伝える2軸の関係位置によって歯車の歯のつけ方は種々に分類される。

(1)2軸が平行である場合　軸に平行に切った歯をもつ平歯車はもっとも普通に使用されている。外かみ合いの場合は軸の回転は互いに逆方向となる。内かみ合いのものはとくに内ば歯車といい、回転は両方とも同方向で、高い減速比を得たいときに使用される。いずれの場合も2軸間の回転数は歯車の直径に逆比例する。すなわち直径の小さい歯車は速く回転し、直径の大きい歯車はゆっくりと回転する。軸に対して歯を傾けて切ったものをはすば歯車という。この歯車は平歯車より回転が滑らかであるが、歯が傾いているために軸方向に荷重がかかり、軸方向の力を受け止めるスラスト・ベアリングが必要となる。軸方向に力のかかるのを防ぐために二つのはすば歯車の歯の向きを逆方向に切って一つの歯車にしたものがある。これをやまば歯車という。やまば歯車は大きな動力の伝達を必要とするところ、また減速比の大きな場合に用いて便利である。特殊な場合として、平歯車の直径を無限大とした場合、すなわち板に歯をつけたものをラックという。これとかみ合う歯車をピニオンといい、ラックとピニオンは回転運動を直進運動に変えたいとき、またはその逆の運動をさせるときに使用される。これにも歯のつけ方によって、はすばと、軸に平行な直線歯すなわちすぐばとがある。

(2)2軸が交わる場合　円錐(えんすい)摩擦車の接触面をピッチ円とする歯車で、傘(かさ)歯車という。歯の切り方により各種の傘歯車がある。円錐の母線に沿って頂点に向かって縮小していく歯形のものをすぐば傘歯車という。また歯を母線に対し傾いて切ったものを曲りば傘歯車といい高速度の回転を伝達するときなどに使用される。

(3)2軸が食い違っている場合　傘歯車では、その2軸を延長すると互いに交差してしまうので軸を延長することはできないが、実際には2軸を延長したい場合もある。こういう場合に用いられるのが食い違い歯車で、その種類はいろいろある。一般には、製作が容易ということから、角度の違う二つのはすば歯車を組み合わせたねじ歯車が用いられる。ねじ歯車は軸間距離の大きいときに便利である。曲りば傘歯車に似たハイポイド歯車は軸間距離があまり大きくないところに用いられ、自動車の後車軸のように軸を食い違わせる必要がある場合に使用される。

　軸が直交し互いに交わらない場合の運動伝達に用いられるのがウォームとウォームホイールである。ウォームの回転速度に対してウォームホイールの回転速度は遅くできるので、速度比の非常に大きいところに用いられる。ウォームからウォームホイールへだけ運動は伝達され、その逆は不可能である。そのほか軸間距離を変えることのできるものに楕円(だえん)歯車がある。また駆動歯車の連続回転に対し、被駆動歯車が間欠的に運動する間欠歯車というものもある。

［中山秀太郎］

歯車の大きさ

歯車の大きさを表すのには円ピッチ（p）、モジュール（m）、直径ピッチ（Dp）などが用いられる。円ピッチはピッチ円の円周を歯数で割った値でミリメートルで表す。ピッチ円の直径をミリメートルで表し、これを歯数で割ったものがモジュールである。寸法がインチの場合には歯数をピッチ円の直径（インチ）で割った直径ピッチが用いられる。mの値はJIS(ジス)（日本工業規格）にその標準値が決められている。歯の大きさはmの値が大きいほど大きくなる。

［中山秀太郎］

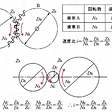
歯車の速度比

駆動歯車Aと被駆動歯車Bがかみ合っているとき、それぞれの毎分回転数をN_A、N_B、ピッチ円の直径をD_A、D_B、歯数をZ_A、Z_Bとすると、速度比（速比）iはi＝N_B/N_A＝D_A/D_B＝Z_A/Z_Bとなる。この場合、歯車AとBとは互いに逆回転する。AとBの間に第三の歯車Cを入れると、AとBの回転は同一方向となり、速度比は、AとBとを直接かみ合わせた場合と同じである。すなわち中間の歯車Cは回転方向を変える役目をするだけで、AとBとの速度比には無関係である。

［中山秀太郎］

歯車の製作

歯車の材料としては鋼、鋳鉄、真鍮(しんちゅう)その他の金属が主であるが、ナイロンその他の合成樹脂を使用するものも多くなった。金属製の歯車には鋳造してつくるものもあるが、多くは歯車切削用の工作機械を使用して切削加工する。歯車を切り出す工作機械を、総称して歯切盤といい、歯車形削り盤、ホブ盤などその種類は多い。歯を切る方法には大別して、型板法、成形法、創成法の3種類がある。型板法は歯の形をした型板に倣って工具を動かして歯を切り出していく方法であるが、歯切りの能率は悪く、大形の歯車をつくるとき以外には用いられない。成形法は、1個の歯みぞの形をしたフライスを用いてフライス盤で切削する。創成法は、切削される歯車と正しくかみ合うラックあるいは歯車の歯形と同じ輪郭をもつ刃物を歯車材とかみ合わせながら相対運動をさせ、連続的に歯を切っていく方法である。現在の歯切り用機械は、ほとんどこの方法によっている。

　円筒の外周に沿ってねじ状の刃をもつホブを用いて歯切りを行うホブ盤は平歯車、はすば歯車、やまば歯車およびウォームホイールなどの歯切りのできる、もっとも一般的な歯切盤で、立てホブ盤と横ホブ盤とがある。ウォームとウォームホイールとがかみ合っているような状態で歯切りが行われる。ホブが回転し、歯車材も回転しながら歯が切られる。ホブには平歯車用ホブ、ウォームホイール用ホブ、そのほかスプライン軸の切削に使用される特殊ホブなどがある。

　歯車を製作するのに転造によることもある。歯車の形をしたダイスの間を素材を通過させ塑性加工で歯車をつくる方法である。素材を加熱しないで行う冷間転造と高周波により加熱して行う加熱転造とがある。生産能率も、ピッチの精度も、歯面の耐摩耗性もよい。しかし、転造できる素材の材質は限られている。そのほか、鍛造ダイスを用いて鍛造して歯車をつくる方法もある。またダイカストにより鋳造してつくることもある。

［中山秀太郎］

[参照項目] | 歯切盤 | 歯車伝動装置

インボリュート曲線とサイクロイド曲線

歯車の各部名称

歯車のおもな種類

歯車の速度比

歯車の切削方法

出典　小学館　日本大百科全書(ニッポニカ)

百科事典マイペディア

歯車【はぐるま】

ギヤ，ギアとも。すべりを伴わずに回転およびトルクを伝えるため，車の周辺に多数の歯を規則正しく設けたもの。二つの適当な歯車を組み合わせて用いる。歯車の歯は，回転を角速度変動なく伝えるための条件を満たした特殊な断面形状のもので，代表的なものにサイクロイド歯形，インボリュート歯形があり，特殊なものにピン歯車歯形などがある。サイクロイド歯形は，互いに接する二つの大きな円をピッチ円（その歯車と同じ働きをすると考えられる仮想の摩擦車を表す円）とし，ピッチ円の内外に接してころがる小さな円を考えたとき，その円周上の一点が描く曲線を連ねて構成した歯形である。インボリュート歯形は，基円（ピッチ円を一定の割合で縮小した円）にまきつけた伸びない糸をほどいてゆくとき，糸上の一点が描く曲線をもって構成した歯形である。インボリュート歯形は，中心距離が狂っても正常運転ができる，容易に正確に製作できる，後に発達した転位歯形の概念により歯数が少ないときの切下げなどの欠点をさけ得るようになった，などの特長があり，摩耗が一様でなく歯形が狂いやすいなどの欠点はあるが，今日，工業的に使われる歯形のほとんどがこれを用いている（インボリュート歯車）。　歯車には，かみ合わせる二つの歯車の軸の相対位置，運動方向，歯すじの形状などによって多くの種類があり，２軸が平行の場合には平(ひら)歯車，斜歯(はすば)歯車，山歯(やまば)歯車などを用いる。２軸が交わる場合にはかさ（傘）歯車を用いるが，これには直歯(すぐば)，曲歯(まがりば)などの種類がある。２軸が食い違う場合にはウォームギヤ，ハイポイド歯車，ねじ歯車などを用いる。また特殊な目的に用いる歯車として，非等速回転を得るための楕円歯車や偏心歯車，間欠運動を得るための間欠歯車などがある。
→関連項目機械要素｜潤滑｜歯車列｜ピニオン

出典　株式会社平凡社

ブリタニカ国際大百科事典 小項目事典

歯車
はぐるま
gear; toothed wheel

ギヤともいう。次々に噛み合う歯によって，回転軸の運動を一軸から他軸へ伝達する機械要素 (部品) の対または単体をいう。軸間距離があまり大きくない場合に用いられる。歯形，歯車軸の相対位置，用途，材料などによって大別される。歯形に関しては，用いられる曲線から，インボリュート歯車，サイクロイド歯車，円弧歯車などに分けられる。歯車軸の相対位置による分類法が一般的で，次の3つに分けられる。 (1) 平行軸　平歯車，はすば歯車，やまば歯車，ラックとピニオンなど。 (2) 交差軸　傘歯車，曲り歯傘歯車，はすば傘歯車，交差軸フェースギヤなど。 (3) 食違い軸　ねじ歯車，ウォームギヤ，ハイポイドギヤ，食違い軸フェースギヤなど (→食違い軸歯車 ) 。用途は手動機械用から航空機用などにいたるまで広い。

歯車
はぐるま

芥川龍之介の最後の短編小説。 1927年に遺稿として発表。自殺寸前の凄絶な心象風景を，視野いっぱいに回転する歯車という印象的な幻覚を軸に描き，狂気の兆候を示すさまざまなイメージと運命的な不吉な暗合とが繰返される。死を賭けて成功した無気味な美と戦慄の表現である。

出典　ブリタニカ国際大百科事典 小項目事典