精選版 日本国語大辞典 「ルジャンドル」の意味・読み・例文・類語
ルジャンドル
日本大百科全書(ニッポニカ) 「ルジャンドル」の意味・わかりやすい解説
ルジャンドル
るじゃんどる
Adrien Marie Legendre
(1752―1833)
フランスの数学者。パリの生まれ(トゥールーズ生まれの説もある)。マザランという名の学校で学び、神父マリJoseph François Marie(1738―1801)から影響を受け、数学へ進んだと伝えられる。ルジャンドルの研究は広い分野にまたがっていた。整数論における業績は輝かしいものであり、著書『整数論』Théorie des nombres(1798)は優れたものであるが、ガウスの論文や著書の出現によってその影に隠れてしまった。楕円(だえん)積分の研究をまとめた全3巻の『楕円関数論』Traité des fonctions elliptiques(1825~1828)も名著に属するが、19世紀にドイツのヤコービとノルウェーのアーベルが、楕円積分そのものではなく、これの定義する関数の逆関数を考えて、ルジャンドルの理論を飛躍的に発展させたので、この名著も影が薄くなった。この悲運の数学者は1833年1月9日にパリの郊外で没した。
[小堀 憲]
ル・ジャンドル
るじゃんどる
Charles William Le Gendre
(1830―1899)
アメリカの外交官。リ・ゼンドルともいい、李仙得とも署名した。8月26日フランスに生まれる。南北戦争に従軍して負傷。1866年厦門(アモイ)領事となり、アメリカ船難破事件で台湾に渡り事件を解決して台湾通となる。1872年(明治5)来日して日本政府顧問となり、琉球(りゅうきゅう)問題解決に台湾出兵を献策した。74年の台湾出兵に際し大久保利通(としみち)に随行渡清(としん)し、中立義務違反として一時アメリカ領事館に拘留された。以後も日本に滞在、北海道開拓論を主張、90年韓国政府顧問となり、99年9月1日ソウルで没。声楽家関屋敏子(せきやとしこ)は孫。
[藤村道生]
『ユネスコ東アジア文化研究センター編『資料御雇外国人』(1975・小学館)』
ブリタニカ国際大百科事典 小項目事典 「ルジャンドル」の意味・わかりやすい解説
ルジャンドル
Legendre, Adrien-Marie
[没]1833.1.9. パリ
フランスの数学者。若いとき学んだマザランという学校の数学教師マリによって数学への道を開かれる。 J.ダランベールの推薦により陸軍士官学校教官となる (1775~80) 。フランス革命には中立的立場を取り,そのため革命政府が創立したエコール・ノルマル・シュペリュール (高等師範学校) やエコール・ポリテクニクの教授にも,子午線の長さを測定する委員会の委員にもなれなかった。 1795年にやっと高等師範学校の教授になる。若い頃回転楕円体の引力について研究し,その覚え書 (83) のなかで,現在ルジャンドルの関数と呼ばれている関数を導入。また『彗星軌道を決定する新方法』 (1806) において,科学史上初めて最小二乗法のまとまった解説をした。しかし,彼の数学上の業績では,ユークリッドの諸命題を整理し単純化し読みやすいテキストに変えた『幾何学原論』 (1794) と楕円積分と整数論の3つが重要であり,彼は 18世紀までの数学と 19世紀以後の数学とのかけ橋の役割を果した。
ル・ジャンドル
Le Gendre, Charles William
[没]1899.9.1. 京城(現ソウル)
フランス生れのアメリカの外交官。リゼンドルともいう。漢名は李仙得。アモイ (厦門) 領事のとき台湾問題に関係し,明治5 (1872) 年来日のとき,副島種臣外務卿の要請で外務省顧問となり,台湾併合を進言。のち韓国政府顧問。
出典 ブリタニカ国際大百科事典 小項目事典ブリタニカ国際大百科事典 小項目事典について 情報
改訂新版 世界大百科事典 「ルジャンドル」の意味・わかりやすい解説
ルジャンドル
Adrien Marie Legendre
生没年:1752-1833
フランスの数学者。パリに生まれ,早くから数学の研究を始める。1782年ベルリン・アカデミーに弾道論に関する論文を提出して賞を得,83年アカデミー・デ・シアンス会員となる。87年パリとグリニジ天文台共同の測地作業に従事し,ローヤル・ソサエティ会員となる。94年共和政下の教育委員会委員長となり,有名な幾何学の教科書を著す。この教科書は多くの版を重ね,各国語にも訳された。そして平行線公理についての考察も見られる。1813年J.L.ラグランジュの後を受けて経度学会員となる。天文学,力学などへの解析学の応用についても多くの業績があるが,主力を注いだのは数論と楕円関数論であった。前者については《数論試論》(1798)とその補訂版《数論》(1830)があり,後者については1825-32年の3巻の《楕円関数論》がある。19世紀初頭まで活動したが,彼自身の数学は18世紀の雰囲気を脱せず,K.F.ガウスの見地に達することはできなかった。
執筆者:弥永 昌吉
ル・ジャンドル
Charles William Le Gendre
生没年:1830-99
アメリカの軍人,外交官。李仙得とも称した。フランスに生まれ,のちアメリカに帰化。南北戦争に従軍し,活躍。1866年厦門(アモイ)駐在領事,73年公使デ・ロングの推薦で日本政府の外務省顧問となり,副島種臣外務卿に台湾併合を進言。74年台湾出兵に当たり蕃地事務局准二等出仕に転じ従軍,米英の中立宣言後も活躍した。90年朝鮮の外事顧問となり,京城で没した。士族授産,殖産興業,市街計画など日本政府への建言書類多数がある。なお,日本滞在中に松平春岳(慶永(よしなが))の庶子と結婚した。
執筆者:広瀬 玲子
出典 株式会社平凡社「改訂新版 世界大百科事典」改訂新版 世界大百科事典について 情報
百科事典マイペディア 「ルジャンドル」の意味・わかりやすい解説
ルジャンドル
→関連項目整数論
出典 株式会社平凡社百科事典マイペディアについて 情報
デジタル版 日本人名大辞典+Plus 「ルジャンドル」の解説
ル=ジャンドル Le Gendre, Charles William
1830年8月26日フランス生まれ。アメリカに帰化し,清(しん)(中国)厦門(アモイ)領事となる。明治5年(1872)来日して外務省顧問をつとめた。のち朝鮮政府顧問。日本滞在中松平慶永(よしなが)の庶子池田糸と結婚。声楽家関屋敏子は孫。1899年9月1日死去。69歳。パリ大卒。漢名は李僊(仙)得。
367日誕生日大事典 「ルジャンドル」の解説
ル・ジャンドル
フランス生まれのアメリカの外交官
1899年没
出典 日外アソシエーツ「367日誕生日大事典」367日誕生日大事典について 情報
世界大百科事典(旧版)内のルジャンドルの言及
【Γ関数】より
…1929年,L.オイラーは定積分に関連して,次の無限乗積を複素数zに対し導入した。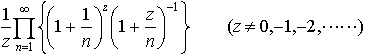 これをA.M.ルジャンドルが,ガンマ関数と命名し,記号Γ(z)を用いた。上の式は,
これをA.M.ルジャンドルが,ガンマ関数と命名し,記号Γ(z)を用いた。上の式は,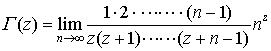 と一致するが,さらに書き直せば,次のワイヤーシュトラスの標準形に変形できる。…
と一致するが,さらに書き直せば,次のワイヤーシュトラスの標準形に変形できる。…
【整数論】より
…またこのことからp-1個の既約剰余類のうちの半分の剰余類に属するものは平方剰余で,残りの半分の剰余類に属するものは平方非剰余であることがわかる。pと互いに素な整数aが,平方剰余であるか,平方非剰余であるかに従って,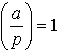 または,
または,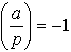 と定め,これをルジャンドル記号という。これに対し,オイラーの規準と呼ばれる次の式,
と定め,これをルジャンドル記号という。これに対し,オイラーの規準と呼ばれる次の式,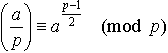 が成り立つ。…
が成り立つ。…
【台湾出兵】より
…1871年琉球宮古島,八重山島の漁船が台湾に漂着し,乗組員多数が原住民に殺害され,さらに73年には岡山県の船員が略奪されるという事件が起こった。このため早くから征韓論を唱えて大陸進出をめざしていた外務卿副島種臣は,これを台湾征討の理由とし,あわせて琉球の帰属問題を国際的に明確化しようとし,前厦門(アモイ)駐在のアメリカ領事ル・ジャンドル(李仙得)を顧問に雇い,その助言によって出兵を計画した。73年6月副島が特命全権大使として日清条約批准書交換のため清に赴いたとき,副使柳原前光をして台湾漂流民の問題を交渉させたが,清国側は,琉球は日本領ではなく,また台湾の原住民は法律の外にあるとし,その処置を拒んだ。…
※「ルジャンドル」について言及している用語解説の一部を掲載しています。
出典|株式会社平凡社「世界大百科事典(旧版)」
関連語をあわせて調べる
〘 名詞 〙 春の季節がもうすぐそこまで来ていること。《 季語・冬 》 〔俳諧・俳諧四季部類(1780)〕[初出の実例]「盆栽の橙黄なり春隣〈守水老〉」(出典:春夏秋冬‐冬(1903)〈河東碧梧桐・高...

