改訂新版 世界大百科事典 「双曲線関数」の意味・わかりやすい解説
双曲線関数 (そうきょくせんかんすう)
hyperbolic function
指数関数を用いて定義される次の6個の関数を総称して双曲線関数という。
双曲線関数は三角関数と類似の性質をもっている。すなわち,coshxとsechxとは偶関数,他は奇関数であり,
sinh xcosechx=1,cosh xsechx=1,
tanh xcothx=1
cosh2x-sinh2x=1,1-tanh2x=sech2x,
coth2x-1=cosech2x
また例えばsinhxとcoshxの加法定理,微分法の公式,べき級数展開は次のようになる。
sinh(x+y)=sinhx coshy+coshx sinhy
cosh(x+y)=coshx coshy+sinhx sinhy
(sinhx)′=coshx,(coshx)′=sinhx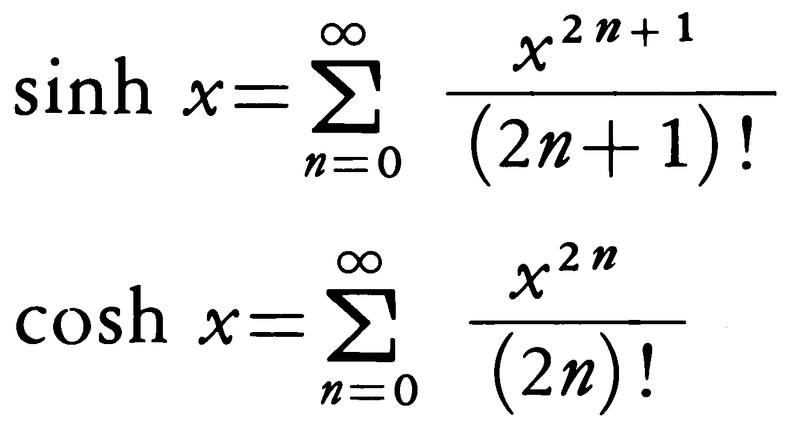
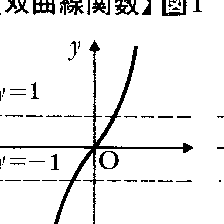
双曲線関数のグラフは図1のようになる。双曲線関数に対して,三角関数のことを円関数ということがあるが,それは次のような両者の類似点による。図2のように,円周x2+y2=1の上の点Pからx軸に垂線PMをおろすと,∠AOP=θ(ラジアン)のとき,すなわち図の扇形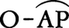 の面積がθ/2のときに,PM=sin θ,OM=cos θとなるが,一方,双曲線x2-y2=1の上の点Pからx軸に垂線PMをおろすと,図の灰色部分
の面積がθ/2のときに,PM=sin θ,OM=cos θとなるが,一方,双曲線x2-y2=1の上の点Pからx軸に垂線PMをおろすと,図の灰色部分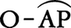 の面積がσ/2のときに,PM=sinh σ,OM=cosh σとなる。
の面積がσ/2のときに,PM=sinh σ,OM=cosh σとなる。
指数関数exの変数xは複素数zに拡張されるから,双曲線関数も複素数zの関数に拡張される。このとき,複素変数の三角関数との間に次の関係がある。
sinhz=-isin iz,coshz=cos iz
tanhz=-itan iz,cothz=icot iz
出典 株式会社平凡社「改訂新版 世界大百科事典」改訂新版 世界大百科事典について 情報


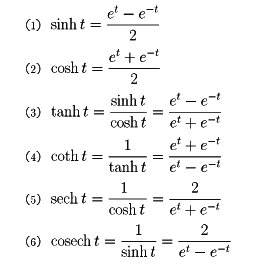
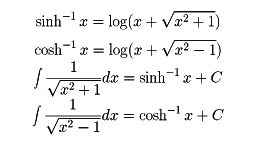
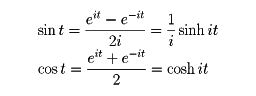

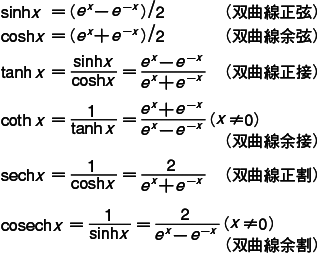 三角関数と類似の性質をもつ理由は,三角関数が複素指数関数で表わせるからで,複素変数の立場では,三角関数の
三角関数と類似の性質をもつ理由は,三角関数が複素指数関数で表わせるからで,複素変数の立場では,三角関数の