推測航法（読み）スイソクコウホウ

デジタル大辞泉

すいそく‐こうほう〔‐カウハフ〕【推測航法】

船舶・航空機で、天体観測や地上物の方位測定によらず、もっぱらコンパスなどの計器によって、現在位置・針路・速度などを割り出していく航法。

出典　小学館

精選版 日本国語大辞典

すいそく‐こうほう‥カウハフ【推測航法】

1. 〘 名詞 〙
2. ① 船舶が、測定儀による航走距離と、羅針儀による針路とによって推測位置を定めて、航海する方法。これだけでは長期にわたっては誤差が増大するので、天測などで補正する。
3. ② 航空機が、機上の計器によって得られたデータ（現在位置・機首方位・風向・風速・高度など）から、つぎの飛行針路・高度・速度を推測して飛ぶ方法。

出典　精選版 日本国語大辞典

日本大百科全書(ニッポニカ)

推測航法
すいそくこうほう

緯度・経度がわかっている地点を起点とし、その後の針路と航程（海里単位で表した航走距離）によって現在船位の緯度・経度を推算したり、緯度・経度のわかっている2地点間の針路・航程を求める算法をいう。中分緯度航法と漸長緯度航法の2法がある。

［川本文彦］

中分緯度航法

仮定に基づく航法で、理論的正確さを欠くが、数百海里以下の航海では誤差も小さく、計算も簡単なので、実用的一般航法として用いられる。

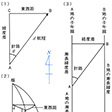
　図の(1)において起点をA、針路をθ、航程をd、到達地点をBとすると、その航走によって生ずる南北方向の距離は、平面三角法によりAC＝dcosθ、東西方向の距離（東西距という）はBC＝dsinθとなる。地球を球と考えると、中心角1分に対する子午線弧長はどこでも同じ1海里であるから、ACは起点と到達点の緯度差となり、起点の緯度に加減して到達点の緯度を求めることができるが、東西距と経度差の関係はそれほど簡単ではない。

　図の(2)のように子午線は極に集合しているので、東西距が同じであってもそのために生ずる経度差は緯度によって異なり、両者の関係は
　　経度差＝東西距×sec緯度
（secはセカントと読み、正割を表す）となる。しかし、船が真東または真西に航走する場合以外は、航走によって緯度も変化するので、この関係は一般的でない。船が任意の針路をとった場合の東西距は、起点と到達点の平均緯度（中分緯度という）における値に等しいと仮定して、
　　経度差＝東西距×sec中分緯度
とするのである。2地点間の針路・航程を求めるには、逆に
　　東西距＝経度差×cos中分緯度
　　tan針路＝東西距÷緯度差
　　航程＝緯度差×sec針路
とすればよい。

［川本文彦］

漸長緯度航法

地球を理論的に正しく相似投影された漸長図上の平面三角を解く算法で、仮定を含まないので、南・北両半球にわたる航海や、長距離航海にも利用できる正確な推測航法である。

　地球の子午線は図の(2)のように極に集合していて、二つの子午線間の間隔は緯度の余弦（cosl）に比例して小さくなっている。この子午線を図の(3)のごとく平行な直線で表すには、子午線間の間隔をその逆数すなわち緯度の正割（secl）倍に示せばよい。

　さらに角度関係が変わらない相似投影にするには、各緯度で子午線間の距離をsecl倍したと同様に、子午線に沿う方向の距離もsecl倍して示せばよい。このような図法では、任意の緯度lの地点は、赤道上の経度1分を基準として、赤道から任意緯度lまでの積分値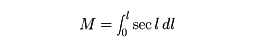

に示せばよく、このMのことを漸長緯度という。このようにしてつくられた海図が漸長図（メルカトル図ともいう）であって、図の(3)のごとく
　経度差＝漸長緯度差×tan針路
とすればよいが、A・B両地の漸長緯度を航海表から求める必要がある。

［川本文彦］

実測との誤差

推測航法によれば、船内で得られる針路と航程のみにより、他に依存することなく随時船位が推算できる（これを推測船位という）が、実際の船位は、海流、潮流等の外力の影響を受けて、時間の経過とともに推測船位から外れていくのが普通で、状況に応じた時間間隔で船位を実測する必要がある。推測船位が実際の船位と一致しない理由は、計算に用いるコンパス針路は船の船首尾線の方向を示すだけであり、測程儀（ログ）による速力は対水速力を示すだけであるからである。船の移動によって生ずる加速度（慣性）を検出して、正確な対地針路・速力が得られれば、随時正しい船位が計算できるわけで、このような航法を慣性航法という。

［川本文彦］

[参照項目] | 慣性航法装置 | 航法 | メルカトル図法

推測航法の原理〔図〕

出典　小学館　日本大百科全書(ニッポニカ)

百科事典マイペディア

推測航法【すいそくこうほう】

自立航法とも。出発点からの針路と航程によって現在位置を推算しつつ進む航法。船では測程儀で航程を知り，これと羅針盤などによる方位をもとに風，潮流，海流などによる影響を修正して推定位置を求める。航空機では風による偏流が避けられないから，対気速度，針路，風向風速などから航跡，対地速度などを計算する。慣性航法も原理はほぼ同じ。
→関連項目航海計器

出典　株式会社平凡社

世界大百科事典（旧版）内の推測航法の言及

【航法】より

…最後の自立航法は，用語としては十分熟しているとはいいがたいが，移動体外の外的基準を必要としない航法で，基本的には針路と距離，あるいは距離と距離による位置決定をもとに，移動体を移動させるものである。古くからある針路と距離(航走日数)とによって位置を推測する方法と原理的には同じであることから，現在でも推測航法と呼ばれているが，実体は測定値の積分によっているので，これによって求まる位置は測定位置といえる。具体的には，針路と速力(距離)によるもの，慣性航法によるものなどがあげられる。…

※「推測航法」について言及している用語解説の一部を掲載しています。

出典｜株式会社平凡社「世界大百科事典（旧版）」