精選版 日本国語大辞典 「相似」の意味・読み・例文・類語
そう‐じサウ‥【相似】
- 〘 名詞 〙
- ① ( ━する ) 形、姿などが、類似していること。
- [初出の実例]「今所謂応同者。非レ言二名体即一故応同一。唯取二其所因義相似一故云二応同一」(出典:法華義疏(7C前)一)
- 「1と2とがそれぞれ自分に似て居るのは、顔の相似を決定すべき主要な本質的の点で似て居るのでなくて」(出典:自画像(1920)〈寺田寅彦〉)
- [その他の文献]〔易経‐繋辞上〕
- ② 似ているがほんとうのものではないこと。にせもの。えせもの。
- [初出の実例]「今の王の権法相似の法を尊んで天子本命の道場たる正法の御寺の御帰依うすくして」(出典:日蓮遺文‐法門可被申様之事(1269))
- ③ 二つの図形が、その一方を一様に拡大または縮小して、他方と合同にすることができる状態にあること。〔数学ニ用ヰル辞ノ英和対訳字書(1889)〕
- ④ 異種の生物の器官で、形態や機能はよく似ているが発生的には起源を異にすること。
- ⑤ 仏語。天台の六即位の第四。さとりによく似た境地に達する段階。相似位。
- [初出の実例]「十住十地分真菩薩、相似以還皆仮名」(出典:顕戒論(820)中)
改訂新版 世界大百科事典 「相似」の意味・わかりやすい解説
相似 (そうじ)
analogy
生物学用語。類縁関係の遠い異種の生物において,個体発生上まったく別の起源から発生し,したがって系統発生的にも無関係の祖先型から別々に生じたものでありながら,一見類似した形態と機能をもつ器官が見られるとき,この類似を相似という。器官の形態と機能が異なっても,その起源が同じであることを指す〈相同〉と対をなすことばで,生物界における類似性を説明する概念の一つ。類似の生活様式をもつ類縁の近い生物の相同器官は,ふつう類似した形態と機能をもつが,この現象はむしろ自明のことであり,相似とはいわない。
相似器官の多くは,類縁の遠い異種の生物が,類似した生活様式をもつように進化した場合にみられる。こうした場合には,それぞれの種類の生活を成り立たせるのに直接関与する諸器官が,類似の機能をもたなくてはならず,そのために当の器官の形態も必然的に類似のものとなる。この現象は平行進化または収れんとよばれるもので,機械的機能をもつ器官に多く見られる。第1は運動に関与する器官で,空中を飛ぶことに適した鳥の翼とセミの羽,水中を泳ぐのに適した魚竜や魚類やクジラの背びれ,地中を掘進するのに適したモグラやケラの前あし,つるになって巻きつくアサガオやフジの茎など,動物にも植物にも多くの例がある。また,ある一つの器官だけでなく,中生代の魚竜とサメとイルカの胴や,メクラヘビとアシナシイモリとミミズの胴のように,全身の体形とその機能が類似する場合も相似の一種とみることができる。
他方,類似した生活様式のもとで,ある器官の生理的機能と形態が収れんして相似を示すことがある。四足動物の目と昆虫の複眼,デンプンを蓄えたサツマイモのいも(根)とジャガイモのいも(茎)などがその例である。しかし,同様の生活様式をもつ類縁の遠い生物に必ず相似器官が発達するわけではなく,むしろ例外的に起こるものである。以上とは異なって,生活様式が類似していない異種の生物が相似器官をもつこともあり,これらは生物体の機械的な保護に関与する体表の器官にしばしば見られる。その例には,硬骨魚のうろこ(骨鱗)とセンザンコウのうろこ(毛の変形),ウニのとげとヤマアラシのとげ(毛),バラのとげ(樹皮)とサボテンのとげ(葉)などがある。こうした相似は生活様式とは関係なく,すべての生物に共通した個体の保存を有利にする傾向によってまったく偶然に一致したものとみるべきであろう。また,いわゆる擬態の例の多くは,形態的には似ていても機能的には別のものであるから相似とはいえないが,アブがハチに似た色彩をもって捕食者をあざむく例などは一種の相似とみることもできる。
以上のように,相似にはひとまずいくつかの種別を認めることができるが,機能と形態がどの程度に似ていれば相似といえるのかについて,客観的な基準があるわけではない。さらに,例えばウニのとげとクリの実のいが,オタマジャクシの尾と精子の尾のように,機能と形態に共通性をもつが,はなはだしくかけ離れた次元にあるものを相似とみなすかどうかについても,よりどころがない。つまり,ある類似が相似であるか否かの判断は多分に各個人の任意の感じ方に立脚するものである。したがって,相似は相同と並ぶ比較形態学の基礎概念であるとしても,科学的に厳密に体系化することのできない便宜的な概念にすぎず,重要さでは相同に遠く及ばない。ただ相似は適応的な進化を暗示する実例として,進化形態学では古くから注目されてきたのである。
→相同
執筆者:田隅 本生
相似 (そうじ)
similar
n次の正方行列A,Bに対してB=P⁻1APとなる正則行列Pが存在するとき,行列AとBは相似であるという。相似な行列の固有値は一致する。
図形の相似
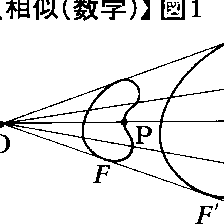
平面上または空間内に一つの図形Fと定点Oが与えられたとし,kは正の定数とする。いま,Fの任意の点Pに対し,OからPに向かう半直線を考えて,その上に点P′をOP′/OP=kとなるようにとれば,PがF上を動くときP′は一つの図形F′を描く(図1)。このとき図形F,F′は相似の位置にあるといい,Oを相似の中心,kを相似比という。また,k>1ならばF′はFをk倍に拡大した図形,k<1ならばF′はFをk倍に縮小した図形という。一般に,二つの図形F,Gに対し,Gと合同な図形F′で,FとF′は相似の位置にあるようなものがとれるならば,図形F,Gは相似であるといい,このことをF∽Gで表す。すべての円,すべての球,すべての正n角形,すべての正n面体はそれぞれ相似である。二つの三角形は次のいずれかの条件が満たされているとき相似である。(1)2組の内角がそれぞれ等しい,(2)3辺の長さの比が等しい,(3)1組の内角が等しく,その角をつくる2組の辺の長さの比が等しい(図2)。二つの図形F,Gが相似であるための条件は,FとGの点の間に1対1対応がついて,対応する角がつねに等しく,対応する長さの比がつねに一定となることである。相似な図形の面積の比は相似比の2乗で,体積の比は相似比の3乗である。
執筆者:中岡 稔
出典 株式会社平凡社「改訂新版 世界大百科事典」改訂新版 世界大百科事典について 情報
日本大百科全書(ニッポニカ) 「相似」の意味・わかりやすい解説
相似(数学)
そうじ
一つの図形を一定点を中心として一定の比に拡大あるいは縮小してできる図形と、初めの図形とは相似の位置にあるといい、その定点を相似の中心、一定の比を相似比という。一般に、二つの図形の一方が、他方を拡大あるいは縮小してできる図形と合同のとき、二つの図形は相似であるという。このとき、拡大あるいは縮小の比をこの二つの図形の相似比といい、一方を他方の相似形という。相似比が1である相似な二つの図形は合同である。二つの図形A、Bが相似であるとき記号A∽Bで表す。辺の個数が同じである二つの多角形で、一方の内角が順次他方の内角と等しく、さらに対応する辺の比が一定であるならば、この二つの多角形は相似である。したがって、辺の個数が同じである二つの正多角形は相似である。
[柴田敏男]
三角形の相似条件
二つの三角形が相似であるための条件は三つある。角角角の相似、辺角辺の相似、辺辺辺の相似の三つである。(1)二つの三角形の対応する二角がそれぞれ等しいとき、残りの角も等しくなり、二つの三角形は相似である。これが角角角の相似である。(2)辺角辺の相似とは、二辺の比とその挟む角が等しい二つの三角形は相似となることで、二辺夾角(きょうかく)の相似ともいう。(3)辺辺辺の相似とは、対応する辺の比が三つとも等しいという条件である。
二つの三角形が相似であることと、円周角の定理や平行線と比例関係の性質を用いて、いろいろな平面図形の性質が導かれる。たとえば、方べきの定理、チェバの定理、トレミーの定理などである。
二つの相似な図形では、対応する線分の比は相似比に等しい。二つの相似な平面図形では、対応する部分の面積の比は相似比の二乗に等しく、二つの立体図形では、対応する部分の体積の比は相似比の三乗に等しい。
[柴田敏男]
相似(生物学)
そうじ
生物学では、相同に対立する比較形態学的概念をいう。2種類の生物のもつ器官が、発生学的起源や解剖学的構造は異なっているのに、同じ機能をもっている場合に、それらの器官の関係は相似であるという。たとえば、同じく空を飛ぶ動物でも、コウモリの膜翼と昆虫のはねとは、その働きは似ているが、前者は肢(あし)の変化したもの、後者は外胚葉(はいよう)性起源であり肢とは関係がない。また、ともにイモとよばれても、サツマイモは根が変形したもので、ジャガイモは茎が変じたものである。相似器官は、同じ働きをすると形態が似てくることを示すもので、進化の証拠となっている。
[川島誠一郎]
ブリタニカ国際大百科事典 小項目事典 「相似」の意味・わかりやすい解説
相似
そうじ
similar
相似
そうじ
analogy
出典 ブリタニカ国際大百科事典 小項目事典ブリタニカ国際大百科事典 小項目事典について 情報
最新 地学事典 「相似」の解説
そうじ
相似
analogy
異なる生物の間で,個体の形態または別々の器官や部分どうしが同じ機能をもつために類似した形態をもつこと。そのような器官を相似器官(analogous organ)という。相同に対立した比較解剖学の基本概念で,R.Owen(1843)によって定義された。今日では系統発生および個体発生において異なる起原をもつことを意味している。例えば魚類と魚竜とイルカは,それぞれ独自な系統であるが,水生に適応した結果,きわめてよく似た体型となっている。相似によって類似した生物群をつくることを収斂
執筆者:小寺 春人
出典 平凡社「最新 地学事典」最新 地学事典について 情報
百科事典マイペディア 「相似」の意味・わかりやすい解説
相似(数学)【そうじ】
相似(生物)【そうじ】
出典 株式会社平凡社百科事典マイペディアについて 情報
普及版 字通 「相似」の読み・字形・画数・意味
【相似】そうじ
字通「相」の項目を見る。
出典 平凡社「普及版 字通」普及版 字通について 情報
世界大百科事典(旧版)内の相似の言及
【オーエン】より
…このころG.L.キュビエから強い影響を受ける。しかし一方でドイツ自然哲学で支配的であった原型archetypeの説もとりいれ,ジョフロア・サン・ティレールの影響を受けて相似analogy,相同homologyという比較生物学上重要な概念を確立した。C.ダーウィン,T.H.ハクスリーヘの敵対者として知られる。…
【相同】より
…また例えば,魚類の胸びれ,鳥の翼,クジラのひれあし,コウモリの翼,ヒトの上肢などの関係がそれである。相同は,異種生物にある起源を異にする器官が一見類似の形態と機能をもつことをさす〈相似〉と並んで,生物界における類似性を説明する比較形態学上の基礎概念の一つであるが,相似よりはるかに重要な意義をもっている。 進化論が現れる前には,動物の比較解剖学は一種の類型学として博物学のなかで重きをなしていたが,その時代にも器官の同一性の追究は中心的な問題であった。…
※「相似」について言及している用語解説の一部を掲載しています。
出典|株式会社平凡社「世界大百科事典(旧版)」
関連語をあわせて調べる
春になって暖かくなりかけた頃、急に寒さが戻って、地面などがまた凍りつく。《 季語・春 》[初出の実例]「七瀬御秡 同晦日也。〈略〉雪汁いてかへる」(出典:俳諧・誹諧初学抄(1641)初春)...