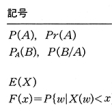数学記号（読み）スウガクキゴウ（英語表記）mathematical symbol

デジタル大辞泉

すうがく‐きごう〔‐キガウ〕【数学記号】

数式を書き表すのに用いる記号。＋、－、×、÷、＝のほか、集合を表す∈や∋、円周率を表すπ、結論を表す∴などがある。

出典　小学館

改訂新版　世界大百科事典

数学記号 (すうがくきごう)
mathematical symbol

計算式3＋4＝7を表すのにわれわれは数字以外に＋，＝という記号を使っているが，このような数学記号の使用の歴史は浅い。＋，＝の使用はそれぞれ15，16世紀までさかのぼるが，最初のうちはおもに代数的な式を表すのに利用され，計算式の中でふつうに使われるようになったのは19世紀である。各時代の人々が必要に応じて数学の記号をくふうしたが，それらのほとんどはすぐに忘れられてしまった。ある記号が一般に定着するのには，皆がその便利さや有効性を認めなければならないので，とくに優劣のないいくつかの記号が考案され，やがてそれら全部が消えてしまうのがふつうであった。記号の利用のしかたは文化圏，学派にもよる。フランスでは今日でも÷のかわりに：を使うことが多い。またわれわれが1,958.65と書くのをヨーロッパ大陸では1.958,65と書き，小数点decimal pointをコンマcommaという。一方では記号のよしあしが数学の進歩に深いかかわりのあることも知られている。微積分学において，I.ニュートンの記号を守り続けたイギリスを，G.W.F.ライプニッツの記号を使ったヨーロッパ大陸が凌駕（りようが）してしまったのは有名な例である。

四則の記号

＋，－，×，÷は15世紀から17世紀にかけてくふうされ使われるようになった。それまでは計算式は記録せず，結果を文章で書くことが多かった。もっとも，エジプト，ギリシア，インドなどでそれぞれの計算記号が使われていたことも確かである。＋，－は15世紀の終りころ使われ始めたようである。1456年にドイツで書かれた原稿でet（andの意）が加法を意味しているものがある。5et7で5＋7を表したのである。このetをくずして，＋が生まれたと考えられている。－はminusのmから考案されたとする説がある。単語の中や記号でmを省略して－を使う習慣があり，minusのmの省略記号としての－が減法の意味に利用されるようになったというのである。他方，2ヤード3インチを2yd－3inと書いて，フィートの単位のところに数がない（0フィート）ことを示す習慣から－が利用されるようになったという説もある。これら＋，－を初めて使った本はウィドマンJ.Widmanの算術書（1489）である。そこでは，＋は超過を，－は不足を意味している。代数学で＋，－を初めて利用したのはオランダのフッケG.V.Hoeckeで，1514年の本に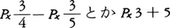という式が現れる。これらは，それぞれ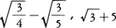の意味である。ドイツのグラマテウスH.Grammateusは18年の本で6pri＋6Nという式を書いているが，これは今日の6x＋6のことである。乗法記号×は1600年ころイギリスで使われるようになった。J.ネーピアの対数についての本の英訳（訳者はライトE.Wright）の第2版（1618）への付録でxが乗法記号に使われた。×を最初に使ったのはオートレッドW.Oughtred（1574-1660）であろうといわれている（1631）。記号×はもともといろいろな意味に利用された。例え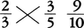ば，あるいは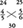，という使い方があった。前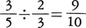者は，後者は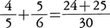 のことである。代数学で×を使うとxと混同しやすいので，aとbの積をabとかa・bで表すことも多い。1522年の本で記号÷が－の意味に使われた例がある。一方，15世紀にはロンドンの金融街ロンバート街では4÷，4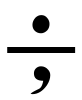で半分を表したという。÷を除法に最初に使ったのはスイスのラーンJ.H.Rahn（1622-76）である（1659）。これはヨーロッパ大陸ではあまり普及せず，アメリカ，イギリスで利用された。

代数方程式

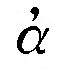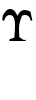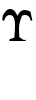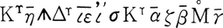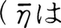
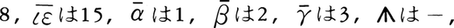
ギリシアのディオファントスは方程式の未知数xとして，数を意味するギリシア語ριθμοςからςを取って使った。x²，x³については，平方，立方を意味する語の頭文字Δ，Kの肩にΥをつけてΔ，Kを利用した。たとえば，で 8x³－15x²＝x³＋2x＋3を表した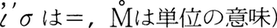。13世紀からイタリアで代数学が盛んになり，方程式の表し方がくふうされた。未知数xにcosa，co，rebを，x²にcenso，ce，quadを，x³にcu，cuboをあてた。たとえば，G.カルダーノはcub'p:6 reb'aeqlis20と記してx³＋6x＝20という方程式を表している（1545）。16世紀のドイツではxに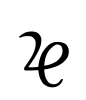（根radixの縮約といわれる），x²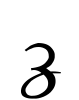に，x³に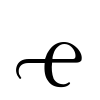などを使った。この記号はイギリスでも使われ，5・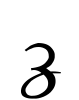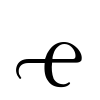・・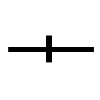20・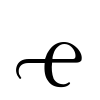・－3・β・で5x⁶＋20x³－3x⁵を表した（1557年のレコードR.Recorde《Whetstone of Witte》）。F.ビエトは方程式の既知量に子音の文字B，C，Dなどを，未知量に母音の文字A，E，Iなどを使い，その文字の式の演算を実行し，代数学の一般的推論を可能にした。彼の方法でA cubus＋B in A quadr.3＋D plano in A，aequatur B cubo 2－D plano in Bはx³＋3ax²＋b²x＝2a³－ab²である。方程式をほぼ現在の形で書くことを提唱したのはR.デカルトであると思われる。彼の記法によれば，x³ax²＋bbx－c³がx³＝ax²＋b²x－c³を意味した（表1）。

微積分の記号

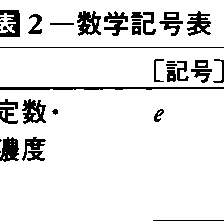
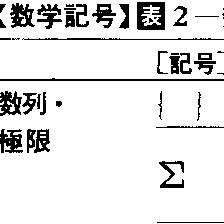
連続的な運動によって変化する量をxで書いたとき，その変化率をẋで表し，ẋの変化率をẍと書いたのはニュートンである。現在の微積分の記号d，∫を考え出したのはライプニッツである。彼はニュートンのẋ，ẍのかわりに\(\frac{dx}{dt}\)，\(\frac{d^2x}{dt^2}\)を使った。dxをxの微小な変化量とみなし，\(\frac{dx}{dy}\)をその変化量の比と考えたのもライプニッツのようである。実際，\(\frac{dx}{dt}\)：
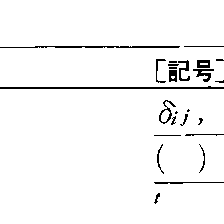
\(\frac{dy}{dt}\)＝ \(\frac{dx}{dy}\)に相当することをいっている。また，関数f（x）の導関数\(\frac{df（x）}{dt}\)をf′（x），\(\frac{d^2f（x）}{dx^2}\)をf″（x）で表したのは，J.L.ラグランジュである。なお，表2（つづき）も参照されたい。
執筆者：丸山 正樹

表1－印刷物にみる代数方程式(( )内…

表2－数学記号表

表2－数学記号表(つづき1)

表2－数学記号表(つづき2)

出典　株式会社平凡社「改訂新版　世界大百科事典」

日本大百科全書(ニッポニカ)

数学記号
すうがくきごう

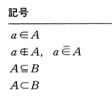
数学の式を書き表すのに用いる記号。算数にあっては、古くは式は書かれず、ことばで計算の手順を示した。この場合、計算記号はほとんど必要なかった。数学記号が必要となったのは、文字を使って式を書き表し、その式を変形する場合である。この点において、数学記号の歴史では、代数学の父といわれるギリシアのディオファントスが重要な地位を占める。彼は加号は用いず、加えるべきものは単に並べて書いて表し、減号には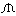のような記号を書いた。数字と文字とを掛けるときには文字のあとに数字を書いた。彼が用いた文字は一つだけだったから、文字と文字とを掛けることはなかった。したがって、乗法の記号も除法の記号も存在しなかった。今日のように加・減・乗・除の記号がそろったのは15世紀から17世紀にかけてである。そのだいたいは次のようであるといわれている。1489年、ウィドマンJ. Widman、過不足の記号として＋、－を用いる。1514年、フッケG. V. Hoecke、加える・引くの記号として＋、－を用いる。1631年、オートレッド、掛ける記号として×を用いる。1659年、ラーンJ. H. Rahn、割る記号として÷を用いる。1557年、レコード、等号として＝を用いる。もちろん、これらの数学記号は個人の発明ではなく、多くの人がいろいろの記号を用い、それらのうち一つが固定して今日に至ったのである。

　このように、初等数学の歴史は長いから、その記号の歴史も複雑である。これに対して、高い程度の数学においては、その記号は、その数学を始めた学者、あるいはそれを発展させた学者が、それぞれの必要に応じて記号を定めたから、その創始者もはっきりしており、その歴史も比較的簡単である。たとえば、現在の微積分の記号d、∫を考え出したのはライプニッツであり、関数f(x)の導関数df(x)/dxをf′(x)で表したのはラグランジュである。

［大矢真一］

数学記号（論理）

数学記号（集合）

数学記号（数）

数学記号（幾何、代数）

数学記号（微分積分、解析）

数学記号（確率）

出典　小学館　日本大百科全書(ニッポニカ)