無理方程式（読み）ムリホウテイシキ（その他表記）irrational equation

デジタル大辞泉

むり‐ほうていしき〔‐ハウテイシキ〕【無理方程式】

未知数についての無理式を含む方程式。

出典　小学館

精選版 日本国語大辞典

むり‐ほうていしき‥ハウテイシキ【無理方程式】

1. 〘 名詞 〙 方程式で未知数についての無理式を含むもの。
   1. [初出の実例]「無理方程式を無理に強付けられては、げんなりして」(出典：平凡（1907）〈二葉亭四迷〉二一)

出典　精選版 日本国語大辞典

改訂新版　世界大百科事典

無理方程式 (むりほうていしき)
irrational equation

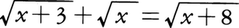のように無理式を含む方程式を無理方程式という。無理方程式を解くには，両辺を何乗かして式を整理し，さらに同様の操作をいくどか繰り返して代数方程式を得，この代数方程式の根のうちで最初の無理方程式を満足するものを求めればよい。最初の無理方程式を満足しない根を無縁根という。上記の無理方程式，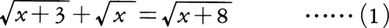

を解いてみよう。（1）の両辺を2乗すると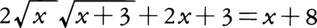，を得，これを整理して，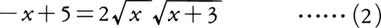

を得る。さらに両辺を2乗すると，

　x²－10x＋25＝4x（x＋3）　……（3）　

を得，整理して，

　3x²＋22x－25＝0　……（4）　

を得る。左辺を因数分解して，

　（x－1）（3x＋25）＝0

を得，（4）の根として，1，－25/3を得る。x＝1は（1）を満足するが，－25/3は（1）を満足しないので無縁根である。このように無理方程式を解く際に無縁根が生ずる理由は無理式を有理化する操作は同値な変形ではないことによる。たとえば上の（2）式から（3）式を得る操作のところに注目すると，（2）式のみならず，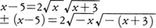

のいずれの式も両辺を2乗すると（3）式になる。－25/3は無理方程式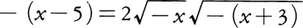，の解である。
執筆者：上野 健爾

出典　株式会社平凡社「改訂新版　世界大百科事典」

日本大百科全書(ニッポニカ)

無理方程式
むりほうていしき

未知数についての無理式を含む方程式を無理方程式という。たとえば、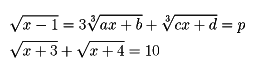

などである。無理方程式を解く際、平方根号や立方根号などを除いて、整方程式にするため、方程式の両辺を平方したり、立方したりすることがある。そうすることによって一般に方程式間の同値性（解集合が変わらないこと）が破れることがある。一般に原方程式の解とならない解が現れることがある。このような解を無縁根という。たとえば方程式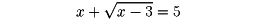

を解くのに、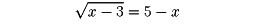

として、両辺を平方して移項すると、二次方程式x²-11x+28=0が得られる。これを解いて解4と7を得る。そこでこれらの解を与えられた方程式のxに代入すると、4は方程式を成り立たせるが、7は方程式の左辺の値を9にするので、成り立たない。したがって4が解となり、7は無縁根である。方程式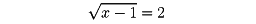

の両辺を平方すると、x-1＝4となり、したがってx＝5となる。5は始めの方程式を成り立たせる。この場合に無縁根は現れない。

　一般にA=BとA²=B²とは同値ではない。後者はA²-B²=(A-B)(A+B)=0だから、後者から二つの方程式A=BとA=-Bの解が得られる。第一の例の無縁根は方程式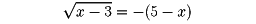

の根であった。無縁根を排除する方法としては式変形ごとに、同値性を保つ条件をつければよい。

　第一の例で原方程式は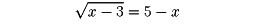

と同値であり、解を実数に限れば（無理方程式では一般にこの立場をとる）、平方根の定義からx≧3,5-x≧0したがってx≦5だから、解は5以下でなければならない。

［竹内芳男］

出典　小学館　日本大百科全書(ニッポニカ)

ブリタニカ国際大百科事典 小項目事典

無理方程式
むりほうていしき
irrational equation

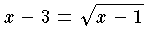未知数の無理式を含む方程式をいう。普通実数のみを扱う。たとえば は無理方程式である。これを解くには，両辺を自乗して
x²－6x＋9＝x－1
x²－7x＋10＝0
これを解いて x＝2 または 5 。しかし x＝2 は与えられた無理方程式の根ではない。これを無縁根という。

出典　ブリタニカ国際大百科事典 小項目事典