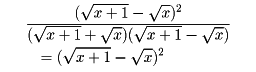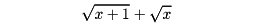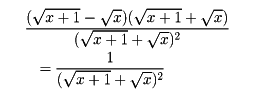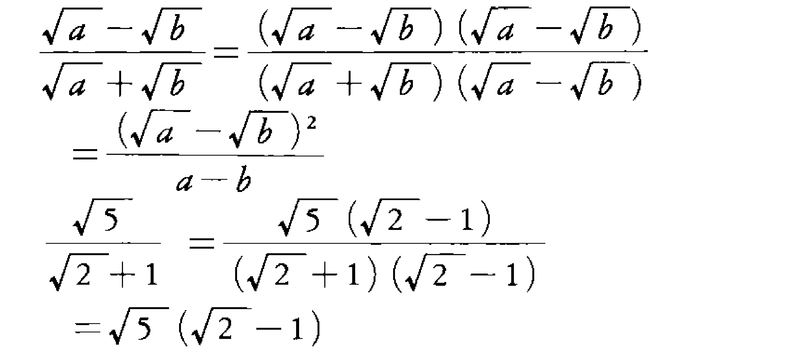有理化（読み）ユウリカ（その他表記）rationalization

デジタル大辞泉

ゆうり‐か〔イウリクワ〕【有理化】

無理式の一部を変形して、根号を含まない式に直すこと。特に、無理数を含む分数式の分母を、無理数のない形に直すこと。

出典　小学館

精選版 日本国語大辞典

ゆうり‐かイウリクヮ【有理化】

1. 〘 名詞 〙 根号を含む式の一部を根号のない形に変形すること。分数の分母の有理化がよく行なわれる。

出典　精選版 日本国語大辞典

日本大百科全書(ニッポニカ)

有理化
ゆうりか
rationalization

無理式において、その式の一部を根号のない形に変形すること。

分母の有理化

でこの分数式の分母・分子に

を掛けると、

となる。

［竹之内脩］

分子の有理化

でx→∞のときの極限値を考える場合、分母・分子に

を掛けて

とすると、x→∞のときの極限値が0であることがわかる。

［竹之内脩］

出典　小学館　日本大百科全書(ニッポニカ)

改訂新版　世界大百科事典

有理化 (ゆうりか)
rationalization

無理式を扱うのに，分母分子に適当な数をかけることによって，分母が根号のない形に変形するのが便利であることが多い。これを分母の有理化という。たとえば，

また無理方程式を解く際に，両辺を何乗かして式を整理し，さらに同様の操作を幾度か繰り返して代数方程式を得る操作も有理化と呼ばれる。このとき得られた代数方程式の根は最初の無理方程式の根ではない無縁根を含むことがあるので注意が必要である。
執筆者：上野 健爾

出典　株式会社平凡社「改訂新版　世界大百科事典」

ブリタニカ国際大百科事典 小項目事典

有理化
ゆうりか
rationalization

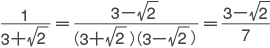根号を含む式，特に平方根を含む分数式の分母から，根号を取り除くように式変形する操作。分母の有理化とも呼ぶ。たとえば，は分母の有理化の操作である。Qを有理数全体の集合としてαを有理数の 2乗では表されないような有理数とする。このとき Q（√α）を，有理数 a，b を用いて a＋b√αと表される数全体の集合とする。Q（√α）は加法，減法，乗法について閉じているが，有理化を用いると 0でない数による除法についても閉じていることがわかる。代数学では，このように加法，減法，乗法および 0でない数による除法について閉じた数の体系を体と呼ぶ。上の有理数全体 Qおよび Q（√α）はともに体であり，Q（√α）は有理数体 Qの 2次拡大であるという。

出典　ブリタニカ国際大百科事典 小項目事典