改訂新版 世界大百科事典 「立体構造式」の意味・わかりやすい解説
立体構造式 (りったいこうぞうしき)
stereostructural formula
分子をつくる各原子の三次元的関係すなわち立体配置，立体配座を明示した構造式。構造式は紙面上にすなわち二次元に表現されるから，立体構造式は，三次元の世界を二次元の世界に投影する手段である。透視式，投影式，立体（ステレオ）図の3種に大別される。
透視式
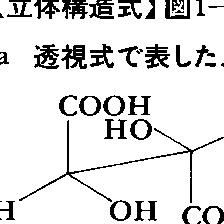
分子を任意の方向から透視して遠近法で表した図式。メソ酒石酸（ねじれ型）の木びき台saw-horse透視式を，図1-a-Ⅰ，a-Ⅱに示す。立体配置，立体配座がよく見てとれる。しかし，透視式は書き方によっては何通りにも読みとれる。たとえば透視式図1-a-Ⅱでは立体配置があいまいである。そこで透視式を書く際，基準平面を定義し，基準平面上の原子と，それより後方にある原子（団）との結合を破線で，それより前方にある原子（団）との結合を太い実線またはくさび印
で，基準平面上の結合は実線で表すことにするとまぎれがない。図1-a-Ⅲはこの約束に基づいて書かれたメソ酒石酸のくさび透視式である。くさびと破線を用いる画法は特定の位置の立体配置を強調するために用いられることがある。たとえば透視式図1-b-Ⅰとb-Ⅱはそれぞれトランスデカリン，シスデカリンを表す。これらは透視式ではないが，一部を透視式で表した立体構造式である。図1-b-Ⅰ，b-Ⅱの表現は，わかりやすいが印刷上面倒な透視式（図1-b-Ⅲ，b-Ⅳ）の代用によく用いられる。
投影式
分子を基準平面に投影して，その三次元構造を表現した立体構造式。不斉炭素原子のまわりの立体配置を表すのに用いられるフィッシャー投影式（またはフィッシャー投影図。1891年E. フィッシャーの提案による）では，不斉炭素原子（1分子中に2個以上の不斉炭素原子がある場合はそのすべて）は基準平面上にあり，不斉炭素原子から左右の方向にでる結合は基準平面から上向きであるのに対して，上下の方向にでる結合は基準平面から下向きであると約束する。この約束に従うと，フィッシャー投影式（図2-a-Ⅰ）は透視式図2-a-Ⅱ（（＋）-乳酸）を表している。不斉炭素2個以上の化合物において，フィッシャー投影式では原則として主鎖をつくる原子をすべて，基準平面上に上下に並べる。したがって，結合の方向は，ある特定の不斉炭素原子についてそれぞれ考える必要がある。現実の分子は主鎖をつくるすべての原子が一平面にのっているのではないからである。フィッシャー投影式はもともと糖類の立体配置を案出するために案出された。その際，糖類につきものの水酸基は不斉炭素原子の左右におくように取りきめられた。この約束によると，メソ酒石酸は図2-b-Ⅰまたはb-Ⅱで表される。b-Ⅰのくさび透視式はb-Ⅲ，木びき台透視式はb-Ⅳとなる。すなわちフィッシャー投影式は重なり形配座を投影したものであり，必ずしも分子の最も安定な状態に対応しているわけではない。R-（＋）-グルコースのフィッシャー投影式は図2-cのようであるが，この投影式のように分子模型を組むと両端がぶつかり合ってしまう。フィッシャー投影式において原子（団）の位置の交換は，実際の分子における原子（団）の位置の交換に対応する。1回の交換は立体配置の反転を意味するので注意を要する。
これに対して，問題とする結合（メソ酒石酸であれば中央の2個の炭素原子）を基準紙面に対して垂直に立てて分子を投影する方式がある。投影式上では中央の2個の原子は重なるので，図2-d-Ⅰ，d-Ⅱに示すようなくふうをする。いずれも，ねじれ形エタンを示す。とくに後者，すなわち問題の結合をつくる原子のうち手前のものを点，後ろのものを円で表す方式は，1950年代にM.S.ニューマンによって導入されたのでニューマン投影式（ニューマン投影図）と呼ばれる。配座解析が盛んになったころに用いられるようになったこの投影式は，分子の立体配座の表現にとくに適しているが立体配置も同時に表現できる。また単結合だけではなく，二重結合の立体配置（幾何異性）も表現できる。図2-e-Ⅰ，e-Ⅱにはフマル酸とマレイン酸のニューマン投影式を示す。しかしニューマン投影式は図2-f-Ⅰ，f-Ⅱ，f-Ⅲに示したメソ酒石酸の三つのねじれ形配座のように，もともと1本の結合のまわりの立体配置の表現のためのくふうであるから，複雑な化合物ではその部分構造の立体化学しか表現できない。そのなかでも図2-g-Ⅰ，g-Ⅱに示したいす形および舟形シクロヘキサンの投影式は，分子構造の対称性のためニューマン投影式が威力を発揮している例である。
ステレオ図
分子模型をわずかに異なる角度から2枚の写真を撮り，これを左右に並べ（図3-a），同時に左右の目で1枚ずつ眺めると立体感覚が得られる。これを立体（ステレオ）写真という。立体写真に基づいて分子の透視式を書けば（図3-b），立体投影式が得られる。立体視したとき左右二つの図がきちんと重なるためにはかなりの精度が要求される。近年コンピューターグラフィックスの発展は，立体投影式の作図をきわめて容易にした。最も有名なのはジョンソンCarol K.Johnsonの手になるオルテップ図である。分子の座標データを入力すれば，任意の方向から見た立体図が出力される。その際，原子の種類や結合の太さなどが自由に変更できる。オルテップ図はX線結晶解析の結果の表記にとくにひんぱんに用いられている。最近ではパーソナルコンピューターの普及により，分子のグラフィック表示がいっそう容易になってきている。
執筆者：竹内 敬人
出典 株式会社平凡社「改訂新版 世界大百科事典」改訂新版 世界大百科事典について 情報