平衡（読み）ヘイコウ（英語表記）equilibrium

デジタル大辞泉

へい‐こう〔‐カウ〕【平衡】

［名］(スル)《「衡」は、はかりのさお》
１ 物のつりあいがとれていること。均衡。「からだの平衡を失う」
２ つりあいがとれて物事が安定した状態にあること。「精神の平衡を保つ」
３ 物体または物質に変化を起こす原因がありながら、それらの効果が相殺し、一定を保っている状態。力学的平衡・熱平衡など。
[類語]平均・釣り合い・均整・調和・釣り合う・見合う・似合う・そぐう・即する・相応・対応・相当・応分・分相応・適合・合致・即応・ぴったり・適う・適する・合う・沿う・当てはまる・当を得る・値する・兼ね合い・均衡・バランス・マッチ

出典　小学館

精選版 日本国語大辞典

へい‐こう‥カウ【平衡】

1. 〘 名詞 〙
2. ① 物体が力学的につり合いの状態にあること。転じて、物事が一方にかたよらないで安定を保っていること。つり合いがとれていること。均衡。
   1. [初出の実例]「原因、近因は蒸発機と収機と其平衡を失へるに在り」(出典：扶氏経験遺訓（1842）一四)
   2. 「平衡を保つ為め」(出典：草枕（1906）〈夏目漱石〉一)
   3. [その他の文献]〔漢書‐律歴志上〕
3. ② たいらなこと。〔新書‐容経〕
4. ③ 人を拝する作法の一つ。上体を直角に曲げ、頭と腰を平らにすること。〔荀子‐大略〕
5. ④ 物質の状態が変化せず、一定の状態に保たれていること。

出典　精選版 日本国語大辞典

改訂新版　世界大百科事典

平衡 (へいこう)
equilibrium

てんびんの二つの皿のそれぞれに物体と分銅をのせて重さを測るとき，分銅の質量がちょうど物体のそれと一致するときに限りてんびんの腕が水平の位置に静止し続ける。これがてんびんによる質量測定の手段であるが，その理由を力学上の原理に求めるならば，〈質点系の各部分に働く力によって生ずべき各質点の変位に対し，この力がなす仕事の総和が0に保たれるような配置がこの質点系の静止の位置を決める〉という仮想仕事の原理がそれに相当する（仮想変位の原理）。このように，運動しうる力学的体系が時間的に変化を受けない持続状態にあることを平衡またはつりあいといい，空間（あるいは相空間）におけるその静止位置をこの力学系の平衡点と呼ぶ。ニュートンの法則に従う力学系では，平衡は上述のように仮想仕事の原理によって定められるものであるが，この平衡の概念は物理学上もっと広範囲に用いられている。一般に，ある物理的体系の各物理量の時間微分を決める運動法則が与えられており，これらすべての時間微分が0に等しいという条件に従っている場合，この体系は平衡にあるということができる。すなわち物理量x₁（t），……，x_n（t）に対する運動法則が，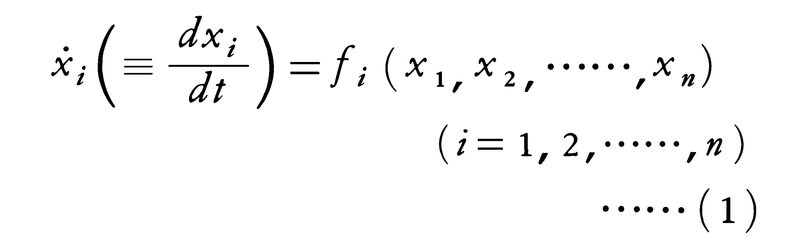

のように与えられているならば（時間tはf_iの中に独立変数として含まれていないとする），

　f_i（x₁，x₂，……，x_n）＝0

　　　（i＝1，2，……，n）　　　　　　　　　……（2）　

を満たすx₁，……，x_nがこの体系の平衡点であり，その点を占めている場合がこの系の平衡状態である。

　しばしば現れる例として化学平衡と熱平衡について略述しよう。数種の化学物質が互いに接触して化学反応が進行するとき，それら反応物質の濃度をx_iと定義して，もっとも簡単な場合（1）のような方程式により反応の進行が記述される。一定時間後，反応の停止した状態は関係するすべての反応物質の濃度に対しẋ_i＝0を意味し，そのときの各濃度が（2）によって求められるが，これがこの反応系に関する化学平衡である。

　熱平衡に関しては，この程度では説明しきれない内容を含んだ重要概念であるが，やはり同様な事情をみることができる。すなわち，ある熱力学的な体系が熱平衡にあるというのは，この体系に大きな熱の供給源が接触して同じ温度に保たれた状態が持続していることを意味する。したがって，もし体系と熱源との間に温度差が生じたとすると，その間に巨視的な規模の熱の授受が行われ，そのとき体系の得る熱量Qの時間微分，すなわちQは0ではない。同様にこの系に対し空間的に電位差が加えられたとすると，その間に巨視的な電流J＝eṙが生じ（eは電気素量），電荷の変位の時間微分ṙが0でない値をとる。すなわち，いずれも体系の内部に物理量の流れが存在するという意味で熱平衡状態からはずれた典型例を与えるものである。

　平衡状態に類似概念でこれより広い意味を含む概念に定常状態があげられる。運動法則（1）についていえば，すべての物理量x_iについてẋ_i＝0の条件に従う状態が平衡であった。もし適当な外的条件によっていくつか（場合によっては単一）の量に対しẋ_i＝一定≠0が保たれているとすると，そのような状態は平衡状態とは異なる非平衡定常状態である。例えば上述の電位差中に置かれた導体でJ≠0なる定常電流が生じていればこれは熱平衡とは異なる定常状態である。

線形安定分析

方程式（2）によって定められる平衡点は一般的に一つとは限らないので，それぞれの特性を調べなければならないことが多い。そのような手段の一つに線形安定分析がある。いま，（2）の根の一つをx_i⁰（i＝1，2，……，n）とし，その点の近傍でのxの運動を考えると，それは（1）の右辺をx⁰のところで展開し，（2）を考慮して，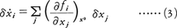

という線形の常微分方程式に従う軌道を調べることに帰着する。（3）の係数行列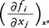の永年方程式の根をλ₁，λ₂，……，λ_nとすると，もしこの行列が相似変換によって対角型に変換されるならば，微分方程式（3）は，

　ẏ_i＝λ_iy_i，すなわちy_i＝exp｛λ_it｝

　　（i＝1，2，……，n）　……（3′）　

のような解をもつ。そして，軌道は平衡点x⁰から出発して時間の経過とともに指数関数的に変化するものの集りで表されることとなり，次のような場合に大別される。

（1）安定平衡（すべてのReλ_i＜0，ここでReは実数部の意味である）　平衡点から出発した軌道群は減衰し，遠くへ離れてしまうことはない（必ず元の平衡点に回帰する）。

（2）不安定平衡（すべてのReλ_i＞0）　平衡点から出発した軌道群は必ず遠くにはずれ元に戻らない。このようなReλ_iはリャプノフ数と呼ばれる。

（3）鞍部点または双曲点（あるReλ_i＞0，またはあるReλ_i′＜0）。

（4）極限円（すべてのReλ_i＝0）　平衡点のまわりに周期軌道群が存在し，初期値がこの平衡点から少しはずれたところから出発すると閉じた軌道をいつまでも描くような運動が持続する。

　近年，このような分析と数値的手段に基づく常微分方程式の解法により，非線形力学系の種々相がくわしく研究されるようになって軌道の構造の解明は著しく進歩した。
→非線形力学
執筆者：長谷川 洋

出典　株式会社平凡社「改訂新版　世界大百科事典」

日本大百科全書(ニッポニカ)

平衡
へいこう
equilibrium

物体（あるいは物質）の状態が時間の経過とともに変化しないで一定であるとき、この物体は平衡にある、または平衡状態にあるという。つり合いともいう。

　外部から完全に孤立した物体、換言すれば外部からの作用をまったく受けない物体が終始平衡状態にあることは明らかである。物体が初めから複数個ある場合には物体系（体系ともいう）として考える。外部からの作用がある場合には、その作用を及ぼす物体を物体系のなかに取り込んで考えることもある。平衡は、力学的平衡、熱（的）平衡、化学（的）平衡に分けて議論されるが、力学的平衡は「つり合い」の項で、化学平衡については「化学平衡」の項で記述しているので、ここでは主として熱平衡について記述する。

［沢田正三］

熱平衡

物体の状態を表す量、数学的にいえば変数のことを状態変数という。この際、物体の状態を外部から規定する変数は外部変数といわれ、この外部変数のもとで決まる物体の状態を表す変数は内部変数といわれる。たとえば、力学的変数では、力は外部変数であり、体積は内部変数である。

　自然界には、「物体系を孤立状態に十分長時間保持すると、物体系の状態変数はそれぞれ時間の経過とともに変わらない一定の値をとる」という経験法則が存在する。この終わりの状態を熱平衡または熱平衡状態という。とくに、物体系がただ二つの物体A、Bからなる場合、この二つの物体が熱平衡にあるときには、物体の熱的状態を規定する熱的外部変数がこの二つの物体で共通になっているのであると考えることは、後述のように、力学的平衡では作用反作用の法則が成り立つことから、まことに自然である。さらに自然界には「物体Aと物体Bとが熱平衡にあり、さらに物体Aと物体Cとも熱平衡にあるときには、物体Bと物体Cとも熱平衡にある」という、三物体間の熱平衡法則がある。結局「熱平衡状態にある物体系を構成する各物体の熱的外部変数はすべて等しい」ということがいえる。この共通の熱的外部変数が、温度というもっとも重要な熱的変数なのである。外部変数と内部変数とはつねに対をなしている。温度という熱的外部変数と対をなす熱的内部変数はエントロピーである。

　物体（または物体系）の安定性を示す尺度はその物体の熱力学関数（熱力学的ポテンシャルともいう）である。これは純力学現象におけるポテンシャルエネルギーにあたるものであって、種々の状態変数の組合せに対して種々のものがある。

　熱力学によると、物体の熱平衡状態においては、その物体の熱力学関数が最小値をとっている。たとえば、等方性物体が温度一定、圧力一定のもとで熱平衡に達すると、ギブス自由エネルギーという熱力学関数が最小値をとる。物体の熱平衡状態は、要するに最安定状態であって、その物体の普通に実現している状態である。

［沢田正三］

力学的平衡

机の上に置かれて静止している物体は、これに働く重力をもって机を押しており、一方、机は抗力をもってこの物体を押している。これらの重力と抗力とはいずれも鉛直線上にあって、前者は下方を、後者は上方を向き、かつ両者の大きさは等しい。この事実は、より一般的には、作用反作用の法則とよばれている。この例で、物体が静止しているのは、物体の状態（例では空間座標）が時間とともに変わらないことであり、すなわち物体は力学的平衡にある。

［沢田正三］

化学平衡

化学的変化の平衡を化学平衡、液相と固相間の変化のような相変化の平衡を相平衡という。化学反応で、可逆反応においておこりうる反応の一方向の速度と、逆方向の反応の速度とがちょうど等しくなって、見かけ上反応がとまったようになることがある。このとき化学平衡の状態になったという。平衡時の成分濃度の比は質量作用の法則に従い、その比は一定の値をとり、平衡定数という。相平衡では、相の境を通しての一方の相から他の相への移行の速度と、その逆方向への移行の速度がつり合ったときに達せられる。

［戸田源治郎・中原勝儼］

『熊井俊彦著『熱力学と化学平衡』（1976・培風館）』▽『H・キャレン著、山本常信・小田恒孝訳『熱力学――平衡状態と不可逆過程の熱物理学入門』上下（1978・吉岡書店）』▽『渡辺啓著『化学平衡の考え方――化学反応はどこまで進むか』（1998・裳華房）』▽『神崎凱・千熊正彦・黒澤隆夫著『化学平衡と分析化学』第2版（2003・広川書店）』

[参照項目] | 温度 | 作用反作用の法則 | 質量作用の法則 | 自由エネルギー | 熱力学 | 平衡定数

出典　小学館　日本大百科全書(ニッポニカ)

岩石学辞典

平衡

平衡とは作用している力がすべて互いに均衡をとる結果，系はいつまでも温度，圧力，化学組成などが同じ状態を連続的に保つ時の系の状態．本来は天秤などで秤量物体と錘との重さが釣り合い，棹が水平になることを意味する．これを拡張して一般にいくつかの物体からなる系が，物体間の相互作用および外力の作用のもとに静止する場合に，系は力学的平衡状態にあるという．この状態では系はいつまでも動かない状態を保っている．この考えを拡張して熱力学では熱や物質の交換，物体内の化学反応を含めて熱平衡の概念となった．熱平衡の概念は狭義には物体間の熱の移動が止まることをいうが，一般には熱力学的関数を極小または極大にする状態である．広義の熱平衡には化学平衡や放射平衡も含まれる．変化があってもその様子が時間的に変わらない場合は定常状態で，平衡状態と定常状態とは区別されるべきであるが，歴史的に両者が混同されている場合もある［長倉ほか : 1998］．岩石学で特に変成岩岩石学では平衡の概念は最も基礎的な概念の一つと信じられている．変成相の概念は完全な平衡状態を仮定したもので，関係する系の各化学成分の化学ポテンシャルの値が一定としている．また相図（平衡状態図）は平衡状態を前提にして作成されたものである．しかし実際の岩石では広い範囲にわたって平衡状態で形成されたものはないので，始めから平衡状態を仮定すると間違いを生じる［鈴木 : 1994］．

出典　朝倉書店

百科事典マイペディア

平衡【へいこう】

釣合とも。物体が外力の作用のもとに静止している（力学的平衡），熱伝達可能な物体の間で熱の移動が起こらない（熱平衡），導体内に電気の移動がない（電気的平衡），化学反応を起こしうる物質間で反応が進行しない（化学平衡），互いに拡散混合する物質間で各物質の濃度が一定に保たれる（濃度平衡）などの場合，一般に系は平衡状態にあるという。系の状態を平衡状態からわずかずらしたとき，系が平衡状態に戻ろうとすればその平衡は安定，そのままとどまれば中立，平衡状態と逆の方向へ進めば不安定な平衡であるという。また小さい変動に対して安定だが，変動がある大きさを越えると不安定になる場合は，準安定な平衡という。
→関連項目温度｜活性化エネルギー｜三重点｜相律

出典　株式会社平凡社

化学辞典 第2版

平衡
ヘイコウ
equilibrium

物体またはいくつかの物体からなる系が，外力あるいは物体間の相互作用のもとに静止している場合，それらは力学的に平衡あるいは釣合いの状態にあるという．平衡状態は安定，中立，不安定の三つに区別される．その区別は，物体を平衡点から微小変化させたときの系の力学的ポテンシャルエネルギーの変化によって示される．図におけるA点，B点，C点はそれぞれ安定，中立，不安定の状態に対応する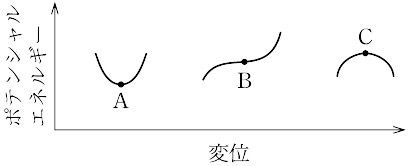．熱力学的系は十分長い時間放置すると，巨視的量に変化がなくなって平衡状態に達する．この状態を熱力学的平衡状態，あるいは単に熱平衡状態という．この概念はさらに拡張されて，電磁場を含む系では場の放射吸収についての放射平衡，化学作用する系での化学平衡をも含んでいる．

出典　森北出版「化学辞典（第2版）」

ブリタニカ国際大百科事典 小項目事典

平衡
へいこう
equilibrium

広い意味では熱平衡のこと。単に熱力学的平衡ばかりでなく，外力と内力との釣合いとか，ポテンシャルエネルギーの極小点，化学反応における平衡などを含む。系が平衡に達しているとき，系は平衡状態にあるという。 (→化学平衡 )

出典　ブリタニカ国際大百科事典 小項目事典

普及版 字通

【平衡】へいこう

バランス。

字通「平」の項目を見る。

出典　平凡社「普及版 字通」