最新 心理学事典 「選択行動」の解説
せんたくこうどう
選択行動
choice behavior
【同時選択手続き】 これは,ハーンスタインHerrnstein,R.J.(1961)が考案した,ハト用実験箱にもう一つのキーを追加して,それぞれを選択肢とした実験手続きで,ここから選択行動研究は始まったといえる。
図1に示したように,並立スケジュールconcurrent scheduleでは,二つのキーやレバー,あるいはタッチパネルを選択肢として,各選択肢に異なる強化スケジュールが配置される。このように,二つの異なる選択肢に強化スケジュールが配置された場合,選択肢間で交替反応が頻繁に起こる可能性がある。これを防ぐため,また二つの選択肢の独立性を保つために,反応を切り替えた直後には強化しない切替反応後強化遅延changeover delay(COD)の手続きを用いる。これは,切替反応が生じてから移行した選択肢では,強化可能状態にあっても一定時間(通常2秒程度)強化が遅延される操作のことである。
2成分から成る並立連鎖スケジュールconcurrent-chains scheduleでは,最初の成分を第1リンク(初環),2番目の成分を第2リンク(終環)とよび,第1リンクには,通常二つの独立した変動時間間隔強化スケジュール(VIスケジュール)を配置する。これに対し,一つのVIスケジュールを用いて,どの第2リンクへ移行するかをあらかじめ決めておく方法もある。これを,強制選択手続きといい,被験体の反応にかかわらず,第2リンクへの移行を選択肢間で等しくすることができる。また,二つの独立したVIスケジュールを用いた方法を自由選択手続きという。並立連鎖スケジュールは,選択期(第1リンク)とその結果受容期(第2リンク)という二つの部分を操作的に区別できる利点があり,選択反応と摂食に至る完了反応consummately responseとを区別できる。
これらの同時選択手続きに対し,選択肢が継時的に呈示される継時選択手続きがフィンドレイFindley,J.D.(1958)により考案され,この継時選択手続きをフィンドレイ型選択手続きという。
【マッチング法則matching law】 ハーンスタインは,ハトを被験体として,並立スケジュールに基づく同時選択手続きを用いて,二つの選択肢の一方では強化率(1分当たりの強化数)を固定し,他方で強化率を組織的に変化させたところ,ハトの二つの選択肢への反応の配分は,二つの選択肢から得られる強化率に一致することを見いだした。これをマッチング法則といい,式⑴または式⑵のように表わすことができる。
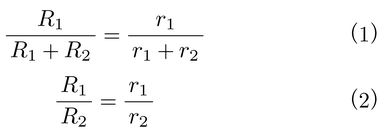
ただし,Rは選択反応,rは強化率を,数字は選択肢1と2をそれぞれ表わす。式⑴と式⑵は代数的に等しい。
図2は,3個体のハトのデータを示しているが,縦軸は式⑴の左辺を,横軸は右辺をそれぞれ表わしている。式⑴の左辺のような形で表現した選択反応を選択率choice proportion,式⑵の左辺のような形の選択反応を選択比choice ratioという。また,選択率や選択比は,被験体の選好preferenceを表わすものである。傾き45度の直線は,式⑴を表わしている。これを完全対応perfect matchingとよぶ。
実際のデータは,しばしばこの直線から逸脱することがある。このため,こうしたデータも扱えるように,式⑶のベキ関数power functionに基づくマッチング法則の一般化が提案された。これを一般マッチング法則generalized matching lawという(Baum,W.M.,1974,1979; 伊藤正人,1983; 高橋雅治,1997)。
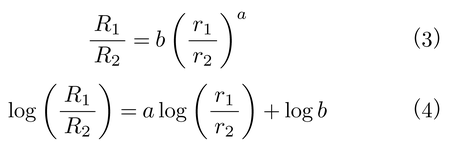
ただし,bは一方の選択肢へのなんらかのバイアス,aは強化率次元に対する被験体の感度を表わす。aが1.0より大きいときは過大対応overmatching,1.0より小さいときは過小対応undermatchingという。その他の記号は式⑴と同じである。式⑷は,式⑶を両辺対数変換し,1次関数の形にしたものである。この式⑷を得られたデータに当てはめて,傾きaと切片log bを推定する。
一般マッチング法則は,ソーンダイクThorndike,E.L.の効果の法則law of effectを定量的な形で表現したものといえるので,これを量的効果の法則とよぶことがある。この法則は,多くの事例で過小対応が見られるものの,強化率だけではなく,遅延時間(Chung,S.,1965),あるいは強化量(Ito,M.,1985)についても当てはまる。また,実験室のハトやネズミはもちろんのこと,野外のハクセキレイの2ヵ所の餌場における採餌行動の分析(Houston,A.,1986),野外のハト集団においてマッチング法則の成立を見いだした研究(Baum,1974)など野外の動物や,幼児の自己制御選択の実験(Ito,Saeki,D.,& Sorama,M.,2009)などヒトについても当てはまる。一般マッチング法則は,強化率や強化量などの強化事象の比が選択反応を決めることを前提としている。つまり,比は同じでも絶対量が異なる場合,たとえば強化量比が3:1で,絶対量が6:2,あるいは9:3の場合には,結果が同じであることを予測するのである。しかし,最近の研究から,絶対量が変わると選択比が一般マッチング法則の予測から逸脱することが明らかになっており(内田善久・伊藤,2000),このことは一般マッチング法則の前提の限界を示すものといえる。
【抗負荷選択contra-free loading】 二つの選択肢のうち,一方をキーつつき反応を必要とする選択肢,他方をキーつつき反応の必要がなく摂食できる選択肢であるとしたら,ハトはどちらを好むであろうか。この場合,キーつつき反応という労働を必要とする選択肢が好まれることが知られている。この事実を抗負荷選択という。内田らは,集団場面において,キーつつきを必要とする餌場(労働餌場)と自由に摂食できる餌場(自由餌場)を設け,ハト4個体の集団全体としてどちらの餌場を好むのかを餌場への滞在時間から調べたところ,キー餌場への滞在時間は,労働餌場がない場合と比べて,若干減少する程度で維持されることが示された。このことは,集団全体として抗負荷選択が起きていることを示すものである(内田・黒島妃香・伊藤,1997)。抗負荷選択の事実は,過小対応が起こることと類似した現象であると考えられている。
【衝動性と自己制御】 強化量と遅延時間が同時に異なっている場合,たとえば遅延時間は短いが強化量は少ない選択肢と,遅延時間は長いが強化量は多い選択肢間の選択を自己制御選択という。一般に,前者の選択を衝動性impulsiveness,後者の選択を自己制御self-controlという(Rachlin,H., & Green,L.,1972)。つまり,目先の小さい利益よりも将来の大きい利益を選ぶことが自己制御なのである。
ラックリンRachlin,H.とグリーンGreen,L.は,自己制御選択場面でハトの自己制御と衝動性を調べた。彼らは,図3に示されているように,即時に得られる2秒間の餌と4秒後に得られる4秒間の餌とを選択肢とする選択場面を基本として,2段階の選択場面を構成した。第1段階の選択では,T秒後に上記の選択場面が呈示されるか,上記の選択肢のうち,4秒後に得られる4秒間の餌という選択肢(自己制御)のみが呈示されるかを決め
るものであった。この選択肢を選ぶことを,あらかじめ自らの選択の余地をなくしておくという意味で自己拘束commitmentという。第2段階は,T秒前に決定した選択場面が前者であれば,選択場面になる。また,後者であれば,選択の余地なく,自己制御を示すことができることになる。ハトは,Tが短いと第1段階の選択で,T秒後に選択場面が呈示される選択肢を選び,この選択場面では,ほとんど即時小強化量の選択肢を選ぶこと(衝動性)が明らかになった。一方,Tが長いと第1段階の選択で自己拘束を選ぶことができた。この事実を,選好逆転preference reversalといい,式⑵を拡張した式⑸に基づいて予測すると,Tが約4秒のときである(Rachlin & Green,1972)。この予測値は,実測データと一致したのである。
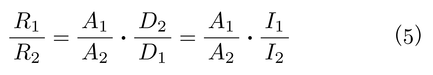
ただし,Aは強化量,Dは遅延時間を表わす。その他は式⑴と同じである。遅延時間は,すぐに得られることが強化事象なので,即時性(I=1/D)で表現できる。
【価値割引discounting】 ラックリンとグリーンの結果は,ハトの二つの選択肢への選好が,時間とともに変化することを示している。すなわち,強化される直前(Tが短いとき:T1)では,即時小強化量選択肢の価値が高く,時間的に離れた時点(Tが長いとき:T2)では,逆に遅延大強化量選択肢の価値が高いと考えられる。すなわち,時間とともに選択肢の価値が割り引かれるのである。これを価値割引という。
図4は,価値の割引(減衰)過程を表わす関数として双曲線関数hyperbolic functionを示している。この関数では,割引過程を表わす曲線が交わる点(選好が逆転する点)が存在する。この双曲線関数に基づく割引過程は,最初は概念的なものであったが,1980年代の終わりごろにハトを被験体としたメイザーMazur,J.E.の実験(1987)により見いだされた。さらに1990年代に入って,ヒトの割引過程について,大学生を被験者としたラックリンらの研究(1991)によって実証された。
ラックリンらは,質問紙を用いて大学生に,さまざまに遅延される1,000ドルと主観的に等価になる,今すぐもらえる仮想の金額(xドル)を答えさせたところ,この等価点が遅延時間が延びるにつれ,式⑹の双曲線関数に従って減少することを見いだした。図5は,遅延時間の関数として仮想の金銭報酬の価値が割り引かれる様子を示している。

ただし,vは割り引かれた報酬の価値,Aは報酬量,Dは遅延時間,kは割引率をそれぞれ表わす。データ(中央値)は,点線で示される指数関数よりも,実線で示される双曲線関数に一致する。したがって,想定されていた価値割引の過程は,双曲線関数で記述できるような減衰過程であることが実証されたのである。その後,双曲線関数的割引過程は,小学生,大学生,高齢者を比較したグリーンらの研究(1994)や,中学生から高校生にわたる青年期の被験者を比較した佐伯大輔・伊藤・佐々木恵(2004)によって確認されている。
【選択行動の数理モデル】 選択といっても,和食にするかイタリアンにするかという同じ行動(食事)間の選択もあれば,食事にするか映画を見るかという異なる行動間の選択もある。後者の選択を扱うモデルがハーンスタイン(1970)により提案されている。このモデルは,マッチング法則を出発点にして,当該の反応に対する強化とその反応以外のすべての反応に対する強化という文脈のもとで,当該の反応の起こり方を扱う点に特徴がある。このモデルは,式⑺のような双曲線関数の形から双曲線関数モデルとよばれている。

ただし,Rは単一の反応,rはその反応に伴う強化事象,reはこの反応以外の反応により得られる強化事象,kは可能な最大反応数である。このモデルは,kとreの二つのフリーパラメータをもつモデルであり,これらのパラメータはデータから事後的に推定するのである(このモデルでは,事前の予測はできない)。
このモデルは,ネズミの走路からハトの実験箱におけるさまざまな実験データ(de Villiers,P.A., & Herrnstein,1976),あるいはヒトの実験室場面から日常場面の行動データ(Beardsley,S.D., & McDowell,J.J.,1992)をうまく記述することができる。この双曲線関数モデルのように,フリーパラメータをもつモデルは,データへの当てはまりがよい(データにうまく当てはまるようにパラメータの値を決めるので当然である)ので,この後もキリーンKilleen,P.(1985)の誘因モデルやラックリン(1993)の価値割引モデルなどが提案されている。一方,このようなフリーパラメータをもたないモデルは,ファンティノFantino,E.(1969)の遅延低減モデルである。このモデルは,フリーパラメータをもたないので,事前の予測が可能であり,並立連鎖スケジュールによる同時選択場面のデータをうまく記述できることが知られている(Fantino,Preston,R.A.,& Dunn,R.,1993; Ito & Asaki,K.,1982)。
【行動経済学の視点】 心理学の選択行動研究と経済学との出会いから誕生した行動経済学behavioral economicsは,行動研究を一つの経済システムと見る新しい視点を提供した。行動経済学の誕生に大きな足跡を残したハーシュHursh,S.R.(1980)は,行動経済学の行動研究への貢献として,⑴行動実験は一つの経済システムとみなせること,⑵強化子は需要の価格弾力性という観点から分類できること,⑶強化子間の関係は代替性substitutabilityや補完性complementarityという概念を用いて記述できること,⑷マッチング法則の成立は代替可能な強化子に限られること,という四つの側面を挙げている。
経済システムとしての行動実験では,給餌が実験セッション内に限られる場合と,給餌が実験セッション外にもある場合を区別する。前者は封鎖経済環境closed economy,後者は開放経済環境open economyとよばれる。この二つの経済環境の区別は,行動への効果が大きく異なることから重要である。たとえば,固定比率(FR)強化スケジュール下の行動は,開放経済環境では,FR値の増加とともにある範囲までは増加し,その後は減少するのに対し,封鎖経済環境では,かなりのFR値まで増加するという相違が認められるのである。封鎖経済環境におけるFR値の増加と行動の増加という関係は,FR値の増加は強化頻度の減少を意味するので,一見奇妙に見える。このことを理解するには,価格と需要の関係を扱う需要分析demand analysisの考え方を導入する必要がある(Hursh,1980; 坂上貴之,1997;恒松伸,1999,2001)。
行動実験に適用した需要分析では,FR値の増加はコストの増加であり,これは価格の増加とみなされる。このような価格を行動価格behavioral priceという。一方,需要(消費量)は,反応数から得られる強化子の総量で表わされる。横軸に行動価格を取り,縦軸に単位時間当たりの強化子数(消費量)を取って描いたものが需要曲線である。需要曲線の傾きは,需要の価格弾力性price elasticityを表わしている。先の例の強化スケジュール下における行動に適用すると,価格の増加(FR値の増加)に伴う消費量(強化子の数)は一定であること,すなわち非弾力的であることが示される。つまり,前述のようなFR値を増加させると反応数も増加するという事実は,消費量を一定にしようとするメカニズムの結果なのである。
価格弾力性という指標は,行動研究で用いられてきた食物や水などの強化子の特性を定量的に区別するために用いられる。ハーシュとネイテルソンNatelson,B.H.(1981)は,封鎖経済環境においてレバー押し反応の強化子としての食物(○)と脳内電気刺激(●)の特性を需要分析により調べたところ(図6),行動価格の増加に対して食物の消費量はほとんど変化しなかったが,脳内電気刺激の消費量は減少すること,すなわち食物は非弾力的であり,脳内電気刺激は弾力的であることが明らかになった。
価格弾力性の指標は,単一の強化子の特性だけではなく,複数の強化子間の関係をも扱うことができる。複数の強化子間の関係を表わす価格弾力性を交差価格弾力性cross-price elasticityという。ハーシュは,アカゲザルの反応を並立VI1分VI1分スケジュールで食物(第1選択肢)と水(第2選択肢)により強化する場面に,第3の選択肢として食物を強化子としてさまざまなVI値のスケジュールにより呈示したところ,VI1分スケジュールで維持されている食物強化子への反応は減少するのに対し,水強化子への反応はむしろ増加することを見いだした。この事実は,第1選択肢の食物強化子と第3選択肢の食物強化子が代替可能な関係にあること,また第2選択肢の水強化子と食物強化子が補完的な関係にあることを示している。
マッチング法則とは,二つの選択肢への行動配分がこれらの選択肢から得られる強化子(消費量)に一致することである(R1/R2=Q1/Q2)。このマッチング法則の式を整理すると選択肢1の価格(消費量に対する反応数)が選択肢2の価格に一致することを表わすものになる(R1/Q1=R2/Q2)。先のハーシュの実験(1978)では,第3選択肢の食物強化子の価格が増加すると,第1選択肢の食物強化子の価格(R1/Q1)は増加したが,第2選択肢の水強化子の価格(R2/Q2)は逆に減少することが示された。このことは,マッチング法則の成立は二つの強化子が食物のような代替可能である特別な場合であり,二つの強化子が食物と水のような補完関係にある場合には成立しないことを示している。 →強化スケジュール
〔伊藤 正人〕
図6 強化子としての食物と脳内電気刺激…
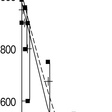
図5 遅延時間(月)の関数としての遅延…

図4 即時小報酬と遅延大報酬の主観的価…
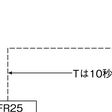
図3 実験手続きの模式図
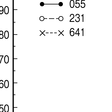
図2 マッチング法則の成立
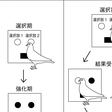
図1 同時選択手続きの模式図
出典 最新 心理学事典最新 心理学事典について 情報

