日本大百科全書(ニッポニカ) 「カタストロフィーの理論」の意味・わかりやすい解説
カタストロフィーの理論
かたすとろふぃーのりろん
水の沸騰するまでのようすを思い描いてみよう。温度計を入れて水温を測りつつ水の状態の変化を観察してみると、沸騰点に近づくまでは水の状態はほとんど変化しないが、ある温度に達すると、それまでの温度変化に比べると、ほんのわずかの変化によって水の状態は液体から気体へと急変する。このように現象の状態を規定している条件(既述の例では温度)のわずかな変化が、状態を一変させる場合を、カタストロフィーとよぶ。カタストロフィーの理論(カタストローフ理論ともよぶ)は、20世紀初頭にポアンカレによって創始された力学系のトポロジー的理論を用いて、このような現象の不連続的な変化をモデル化するものであり、とくに生物学への応用に力点を置いて提唱された。フランスのトポロジストのR・トムは、1960年代からトポロジーとくに写像の特異点の理論、およびその数学以外の対象(とくに生物)への応用を目ざしてカタストロフィー理論を構築し、1972年に『構造安定性と形態形成』を刊行したが、この本こそ今日のカタストロフィーの理論の誕生を告げるものである。トムと並んでイギリス人のクリストファー・ジーマンが、とくにその応用面で活躍し、人文科学への応用についてもいろいろ考察している。
従来の、微分方程式論を主要な武器とする解析的手法にとって、カタストロフィー現象の数学的解明は不得手であった。条件の微少変化に状態が滑らかに依存するような現象を議論の中心に据えていたからである。トムはカタストロフィー現象の解明に、自らもその創始者の一人である微分トポロジー(定量的な性質と定性的な性質の間の深い層での関連を調べる数学)の手法を用い、カタストロフィー現象の定性的分類に成功したのである。以下順に、問題の定式化、いわゆる初等カタストロフィーの分類定理とその簡単な応用について述べる。
[野口 廣]
カタストロフィー現象の定式化
ジェットコースターの軌道のように状態が一次元的に記述される場合を考えてみよう。このコースの各点の上にそっとボールを置いてみる()。明らかにA、C、Fの点に置かれたボールは左または右に転がり始めるであろう。一方BやEに置かれたボールは安定してその位置に止まる。Dに置かれたボールは峠が平らならばその位置に止まることも可能であるが、わずかの力の不均衡でもBやEの方向に転がり落ちてしまうであろう。B、Eの点を他の点と区別しているのは、この2点がボールの重力によるポテンシャルエネルギーの極小値を与える点であるということである。実はこの曲線は四次の多項式として表される。三次以下の係数をすこしずつ変えていくとのような曲線族を構成することができる。最初s1で安定しているボールの動きを考えてみよう。曲線は、初めのうちはs1でのみ極小値をとるが、徐々に右方にも極小値が現れ、ある瞬間に左方の極小値は消失して、状態はs1からs2に急変する。この例は、カタストロフィー理論における自然現象のとらえ方、カタストロフィーのおこり方などを端的に示したものである。
自然現象のシステムの状態は、適当にモデル化されて、多次元空間の中に座標を設定して表される。もちろんすべての状態が等価なのではない。ポテンシャルとよばれる空間上の関数の極小値を与える点のみが実現されうる点である。そのポテンシャルは、外部条件によって滑らかに制御(コントロール)されている。コントロールもまた適当な空間内の座標によって表され、その空間の次元をコントロールの数とよぶ。コントロールの微少変化はポテンシャルの微少変化を生むが、ポテンシャルの極小値を与える点の分布は急激に変動する可能性がある。このとき、現象にカタストロフィーがおこると考えるのが、カタストロフィーの理論の「カタストロフィー」観である。したがってカタストロフィーの定性的分類をすることは、コントロールに依存するポテンシャル族の極小値の分布の状態を分類することにほかならない。
以上の問題の定式化のもとに、トムによる初等カタストロフィーの分類定理を次のように述べることができる。考えているシステムの状態はn個(nは任意の自然数)の変数で表され、コントロールの数は4以下である。これらを変数とするポテンシャル関数が与えられている。このシステムにカタストロフィーがおこったとすると、状態とコントロールの変数に適当な変数変換を行えば、そのポテンシャルはにあげた七つの関数のいずれかに変換される。ここで注意すべき点は、変換されたポテンシャルの状態変数はxかyで示すことができる。すなわち、適当に選ばれた新しい1個か2個かの変数のみで状態が完全に示されるのである。また、コントロールは新ポテンシャルではa、b、cかdで示すことができる。ポテンシャルの式でプラス・マイナスがある場合は、そのどちらかになるということであり(したがって、カタストロフィーは細かくいえば七つではなく10個あることになる)、マイナスのほうを、プラスのほうのカタストロフィーの、双対(そうつい)のカタストロフィーという。
[野口 廣]
カタストロフィーの例
座屈におけるカタストロフィー
細長い棒や薄い板などを圧縮すると、ある荷重で、突然横方向にたわみを生じ、以後たわみが急激に増大する現象がおこる。これを座屈というが、この座屈をカタストロフィーの理論で説明してみよう。
の(1)のような二つの剛体のアームが、水平に保たれるように中央でスプリングにより留められている。このアームの端は左右のみに動き、上下には動かないようになっているとする。(1)のように水平力βが徐々に加えられると、βがある臨界値に達するまではなんの変化もないが、臨界値に達すると、このアームは上方(または下方)に(2)のように座屈する(第一の座屈)。さらにβを増すと座屈の度合いも増えてくる。その大きさは図のように角xで示される。今度は水平力を固定し、両アームに垂直荷重αを徐々に加える((3))。αがある臨界値に達するとアームは(4)のように下方へと座屈する(第二の座屈)。このシステムでのアームの長さを1とする。システムに蓄えられる全エネルギーVは、もっとも一般的な場合の(3)の図から
V=2μx2+αsinx-2β(1-cosx)
である。ここで(1/2)μがスプリングの弾性係数である。このポテンシャルはsinxやcosxのテーラー展開を用いて近似計算すると
F=(1/4)x4-ax-(1/2)bx2
となるので、アームの座屈はのような楔(くさび)のカタストロフィーを用いて説明できる。ここでaとα、bとβとは定数の差を除いて比例している。水平力βと垂直荷重αの変化につれて、コントロール平面上の点(α,β)が点線で示した曲線上を①、②、③、④と動いていくにつれて、アームの状態は、コントロール平面の曲線上にある曲面S上の点線で示した曲線上を変化する。つまり(1)でxは0で、(2)で突然あるプラスの値(第一の座屈)になり、(3)までxはプラスで値は増え続け、(4)で突然xはプラスからマイナスへと二重矢印で示したカタストロフィー(第二の座屈)をおこし、急変することが示される。
これは単純なアームの座屈の説明としてカタストロフィーの理論を用いた例であるが、一般の複雑な構造物の座屈の現象も同様に考察されている。また、同様に考察すると、両端を固定した弾性体の棒に垂直加重を加えたときにこれが崩壊する際の加重の臨界値は、荷重を加える点が棒の中心にあるとき最大で、中心からε%だけ離れたときの臨界値は、のような楔形のグラフで示されることも、このカタストロフィーの理論を用いて示すことができる。
[野口 廣]
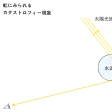
コースティックスにおけるカタストロフィー
太陽の光がコーヒーカップに反射してコーヒー面上にのような楔形の線が輝く。このように光線や音が反射や屈折をした結果、ある図形上に光や音が集中する現象がコースティックスである。これもカタストロフィーの理論を用いて解明することができる。虹(にじ)はのように太陽光線が水滴で反射屈折した結果できるもので、折り目のカタストロフィーによる現象である。レーザービームなどの平行光線を不規則なレンズで屈折させるといろいろな図形のコースティックスが現れるが、空間中では、局所的には放物的へそのカタストロフィー以外の初等カタストロフィーと関連した図形が現れ、平面では、折り目と楔のカタストロフィーに関連する、普通の曲線と楔形の曲線からなる図形が現れることが示されている。こうした理論は、結晶格子の散乱現象にも応用されている。
[野口 廣]
囚人の暴動におけるカタストロフィー
以上のような物理科学への応用と同時に、ジーマンはカタストロフィー理論の人文科学への応用を試みている。たとえば、1972年にイギリスのガートリー刑務所における暴動の解析を行い、その結果、刑務所の状態は不穏か平穏かであり、この状態は刑務所内の緊張と不和とがコントロール要因となっていることを確かめ、のような楔のカタストロフィーのモデルを提唱した。すなわち、刑務所内での単調さに飽きて、なにか刺激を求めて不和がおこると緊張が高まり、また新しい不和が加わり、さらに緊張が高まると……と事態が推移する。コントロール平面上をその時点の不和と緊張を示す点がしだいに右上Aより左下Bへと動いていき、ついに点Cで楔のカタストロフィー曲面の折り目の線の像と交わる。ここで、状態を示す曲面上の曲線は、曲面の下方の平穏状態から二重矢印のように一気に上方の不穏状態を示す部分へと跳び上がり、ここに暴動のカタストロフィーがおこる。こうした解析の結果を用いて、監視システムをつくり、連続的にデータを解析分解した結果、暴動を予知することができたと報告されている。
カタストロフィーの理論は、この暴動のモデルのほか、株式市場の暴騰・暴落のモデルや、動物の気分の解析、心理学などにもいろいろと応用されている。
[野口 廣]
『野口廣著『カタストロフィーの話』(1976・NHKブックス)』▽『I・スチュワート、T・ポストン著、野口廣他訳『カタストロフィー理論とその応用 理論編・応用編』(1980、1982・サイエンス社)』
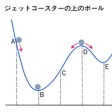
カタストロフィー現象の定式化(1)〔図…
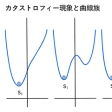
カタストロフィー現象の定式化(2)〔図…

初等カタストロフィーの分類と七つの関数…
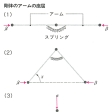
カタストロフィーの例(1)〔図C〕
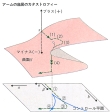
カタストロフィーの例(2)〔図D〕

カタストロフィーの例(3)〔図E〕

カタストロフィーの例(4)〔図F〕
カタストロフィーの例(5)〔図G〕

カタストロフィーの例(6)〔図H〕

