ガウスの定理
がうすのていり
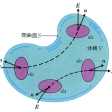
一般にベクトルvの場で、一閉曲面Sに囲まれた空間Rを考えたとき、この曲面上で外向き法線上の単位ベクトルをnとし、直交座標系の基本ベクトルをi、j、kとすれば、(v・n)の面積積分は
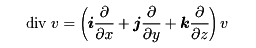
の空間全体に対する体積積分に等しいという定理。つまり
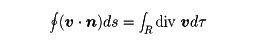
この定理は電磁気学では、電気に関するガウスの定理としてとくに重要である。つまり、真空中の静磁場内で任意に閉曲面を考えるとき、この閉曲面を貫く全電場束は、その面内にある全電荷の代数和の4π倍に等しいことが導かれる。電場ベクトルをEとすれば、
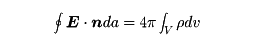
ここで右辺の積分は、閉曲面Sによって囲まれた体積V内の全電気量を意味する。またこの定理の微分形として
div E=4πρ
がある。同様に磁気に対するガウスの定理は
div H=4πρm
となる。なおここでρおよびρmはそれぞれ電荷および磁化密度である。
[安岡弘志]
出典 小学館 日本大百科全書(ニッポニカ)日本大百科全書(ニッポニカ)について 情報 | 凡例
Sponserd by 
ガウスのていり
ガウスの定理
Gauss’ theorem
ベクトルvの場において,閉曲面Sによって囲まれた空間Vを考えたとき次式で表される関係をいう。
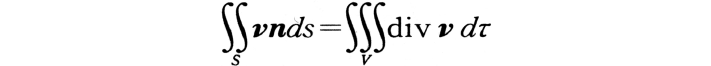
ここで,nはSに関する外法線上の単位ベクトルであり,dτは体積要素を意味する。特殊な場合として,重力場を考え,閉曲面として地表面をその一部とする十分大きな曲面を考える。このとき地下の質量過剰(不足)MとMに起因する地表の重力分布との間に得られる次式,
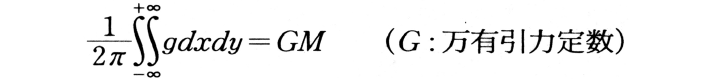
の関係を単にいう場合がある。
執筆者:瀬谷 清
出典 平凡社「最新 地学事典」最新 地学事典について 情報
Sponserd by 
ガウスの定理
ガウスのていり
Gauss' theorem
ガウスの発散定理または単に発散定理ともいう。ベクトル解析における定理。いくつかの閉曲面で囲まれた有界な領域を V とするとき,ベクトル場 F が V およびその境界面 S 上で連続な偏微分係数をもてば,ベクトル場 F の発散 divF の V における体積分は,境界面 S の法線方向への F の成分の面積分に等しい。すなわち
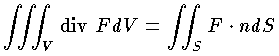 である。ここで n は,S の単位法線ベクトルであり,S の内部から外部に向うものとする。
である。ここで n は,S の単位法線ベクトルであり,S の内部から外部に向うものとする。
出典 ブリタニカ国際大百科事典 小項目事典ブリタニカ国際大百科事典 小項目事典について 情報
Sponserd by 
法則の辞典
「ガウスの定理」の解説
ガウスの定理【Gauss' theorem】
(1) あらゆる条件のもとで,ベクトル関数の発散の体積(V)での体積積分は,そのベクトル関数の外向き法線成分 V の境界面上の表面積分に等しい.すなわち次式となる.
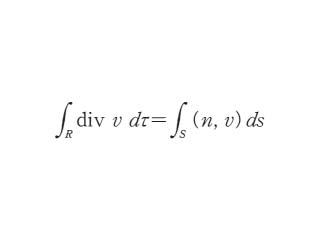
(2) 「極値定理」,すなわち調和関数はその正則な領域の内部においては極大や極小をとることはない.閉領域において正則な調和関数が極値をとるのは,必ずその領域の周辺上の点においてであるという定理.
(3) 曲面の点における二つの主曲率の積は,曲面の一つの不変量である.この積のことを「ガウスの曲率」という.
出典 朝倉書店法則の辞典について 情報
Sponserd by 
世界大百科事典(旧版)内のガウスの定理の言及
【調和関数】より
…これを平均値性質という。逆に,連続性の仮定の下に,この性質をもつ関数は調和関数である(ガウスの定理Gauss’ theorem)。 uがDで調和のとき,uが定数でないかぎり,uはDにおいて最大値も最小値もとらない。…
【ベクトル解析】より
…また,閉曲面Sで囲まれた領域Vがあるとき,体積要素をdVと書くことにすると,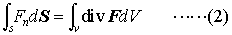 が成立する。これをガウスの定理という。Fが流速ベクトルのときは,(1)の左辺はCに沿う循環を表し,(2)の左辺はSを通って単位時間にVから流出する流量である。…
が成立する。これをガウスの定理という。Fが流速ベクトルのときは,(1)の左辺はCに沿う循環を表し,(2)の左辺はSを通って単位時間にVから流出する流量である。…
※「ガウスの定理」について言及している用語解説の一部を掲載しています。
出典|株式会社平凡社「世界大百科事典(旧版)」
Sponserd by 
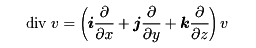
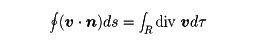
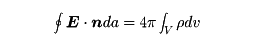


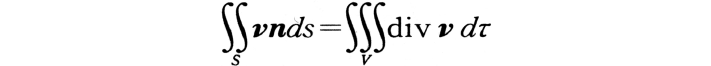
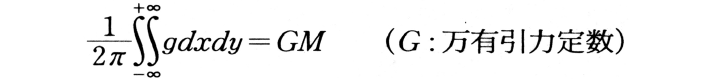
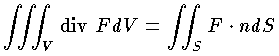 である。ここで n は,S の単位法線ベクトルであり,S の
である。ここで n は,S の単位法線ベクトルであり,S の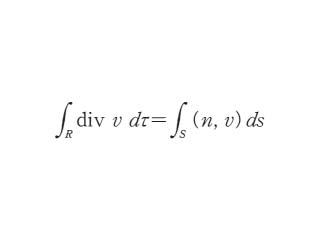
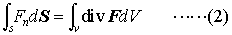 が成立する。これをガウスの定理という。Fが流速ベクトルのときは,(1)の左辺はCに沿う循環を表し,(2)の左辺はSを通って単位時間にVから流出する流量である。…
が成立する。これをガウスの定理という。Fが流速ベクトルのときは,(1)の左辺はCに沿う循環を表し,(2)の左辺はSを通って単位時間にVから流出する流量である。…