ベイズの定理 (ベイズのていり)
Bayes' theorem
ベーズの定理ともいい,イギリスの数学者ベーズThomas Bayes(1702-61)にちなむ。全体が排反事象H1,H2,……,Hk,……に分かれていて,それらは起こりうる仮定を表しているとする。このときEという事象が観測されたとしよう。Hiが起こったと(その確率P(Hi)は0でないとする)Eの条件付き確率P(E/Hi)は,
P(E∩Hi)/P(Hi)
で表され,また仮定から,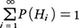 だから,確率の計算,
だから,確率の計算,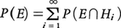 により,
により,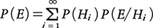 を得る。
を得る。
よってP(Hi/E)=P(E∩Hi)/P(E)
に上式をあてはめて,
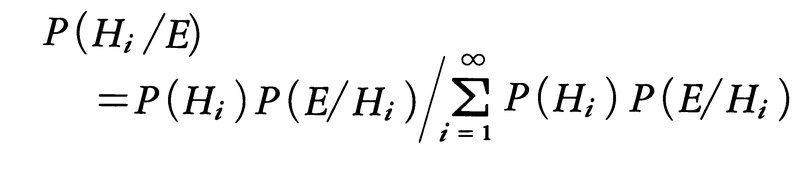
が得られる。これがベイズの定理で,Eが観測されたという条件のもとで仮定Hiの確率P(Hi/E),すなわちHiの事後確率を与えるものである。P(Hi)は事前確率とも呼ばれる。例えば全国の家庭を調べ,ちょうどi人の子どもをもつ(仮定Hi)確率がpiだとする。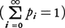 。いまそれが男子ばかりの家庭であることがわかったとき(これを事象Eとする),ひとりっ子の家庭(すなわちH1)である確率P(H1/E)を求めよう。一般に男女の出生率に違いがないとしてよいとすれば,i人の子どもがあって全部男子という確率は1/2iと考えられる。すなわちP(E/Hi)=1/2i。よってベイズの定理から,ひとりっ子である事後確率は,
。いまそれが男子ばかりの家庭であることがわかったとき(これを事象Eとする),ひとりっ子の家庭(すなわちH1)である確率P(H1/E)を求めよう。一般に男女の出生率に違いがないとしてよいとすれば,i人の子どもがあって全部男子という確率は1/2iと考えられる。すなわちP(E/Hi)=1/2i。よってベイズの定理から,ひとりっ子である事後確率は,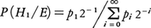 である。ところが,このベイズの定理に対して,形而上学的な見地から,機械的に応用することに強い批判がある。事前に情報がないときは,起こりうるいくつかの可能性はすべて同程度に確からしいとすることに問題があるからである。これまで5000年の間,毎日太陽は東から昇った。明日も東から昇る確率はいかにといった例を考えたらその理由が推察される。具体的な問題に応用するときには注意が必要である。
である。ところが,このベイズの定理に対して,形而上学的な見地から,機械的に応用することに強い批判がある。事前に情報がないときは,起こりうるいくつかの可能性はすべて同程度に確からしいとすることに問題があるからである。これまで5000年の間,毎日太陽は東から昇った。明日も東から昇る確率はいかにといった例を考えたらその理由が推察される。具体的な問題に応用するときには注意が必要である。
ベイズの定理は一般化され,数理統計学で用いられるときは次のような形で述べられる。それはパラメーターθをもつ確率変数Xの分布の密度関数f(x/θ)と,θの事後分布の密度関数p(θ/x)との関係を示すもので,θの事前分布の密度関数がp(θ)ならp(θ/x)は,
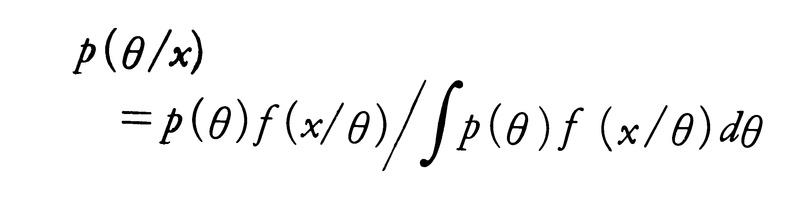
で与えられることを主張する。これもよく用いられるにもかかわらず,事前確率が数値的に明確でないときに用いることの批判を巡って,かなりの論争があり現在も続いている。
執筆者:飛田 武幸
出典 株式会社平凡社「改訂新版 世界大百科事典」改訂新版 世界大百科事典について 情報
Sponserd by 
ベイズの定理
べいずのていり
k個の事象E1、E2、……、Ekがあって、このうちのどの二つも同時におこることはなく、k個のうちのどれか一つがかならずおこるとする。このとき、事象Eに対して
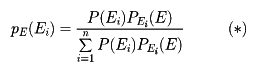
が成り立つ。これを発見したイギリスのベイズThomas Bayes(1702―61)にちなんで「ベイズの定理」という。前記の式の右辺の分母は、仮定によって
P(E1∩E)+P(E2∩E)+……
+P(Ek∩E)
=P((E1∪E2∪
……∪Ek)∩E)=P(E)
である。一方、分子はP(Ei∩E)に等しいから前の等式が成り立つ。前記の等式(*)の右辺と左辺では、条件づけに用いられている事象が入れ替わっていることに注意されたい。
この定理は応用が広い。いまk個の原因が考えられてその一つ一つの原因がおこるという事象をE1、E2、……、Ekとする。Eiという原因がおこった場合に、事象Eがおこるという条件付き確率がpEi(E)であり、逆に事象Eがおこった場合にそれがEiのもとでおこったという条件付き確率がpE(Ei)である。このように考えて、p(Ei)を事前確率、pE(Ei)を事後確率という。ベイズの定理は統計的推論を行うとき重要な役割を演ずる。
[古屋 茂]
出典 小学館 日本大百科全書(ニッポニカ)日本大百科全書(ニッポニカ)について 情報 | 凡例
Sponserd by 
ベイズの定理
ベイズのていり
Bayes' theorem
確率論における重要定理の一つ。ある現象 B のすべての可能な原因 A1,A2,…,An があるとき,各原因の生起確率 (事前確率) Pr(Ai)(i=1,2,…,n) ,およびその原因のもとでの B が生起する条件つき確率 Pr(B|Ai) から,逆に,結果である現象 B が起ったもとでの各原因 Ai が真である確率 (事後確率) Pr(Ai|B) を求める公式は次式で表わされる。
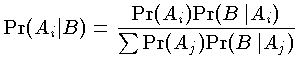 結果から原因の確率を逆算することができる点が興味深く,応用例もきわめて多い。証明は,条件つき確率そのものであって,まったく容易であるが,上記のように,深い哲学上の因果律を負わせることに反対する意見もある。 T.ベイズ (1702~61) はイギリスの牧師である。逆確率の定理ともいわれる。
結果から原因の確率を逆算することができる点が興味深く,応用例もきわめて多い。証明は,条件つき確率そのものであって,まったく容易であるが,上記のように,深い哲学上の因果律を負わせることに反対する意見もある。 T.ベイズ (1702~61) はイギリスの牧師である。逆確率の定理ともいわれる。
出典 ブリタニカ国際大百科事典 小項目事典ブリタニカ国際大百科事典 小項目事典について 情報
Sponserd by 
法則の辞典
「ベイズの定理」の解説
ベイズの定理【Bayes' theorem】
確率は事象の列よりも個々の事象,あるいは命題に関係したものと考えた,統計的推論や意志決定に関する定理である.条件つき確率を相互変換するのに用いられる定理.
出典 朝倉書店法則の辞典について 情報
Sponserd by 
世界大百科事典(旧版)内のベイズの定理の言及
【確率】より
…任意の事象Aに対して,関係式P(A)=P(A∩H1)+P(A∩H2)+……+P(A∩Hn)と,P(A∩Hi)=P(A)P(Hi/A)=P(Hi)P(A/Hi)を用いてP(A∩Hi)/P(A)をかき直せば,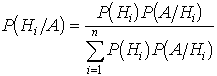 が得られる。これがいわゆる
が得られる。これがいわゆる[ベイズの定理]である。 条件付き確率の特別な場合として,事象AとBが独立な場合のPA(B)を考えよう。…
【数理統計学】より
…さらに分散や高次モーメントをはじめ,今日の数理統計学の基礎となるいくつかの概念を導入し,その役割を明らかにした。これらラプラスやガウスの研究には,1763年に公にされたベイズの定理が支えになっており,原因から結果の生ずる確率があらかじめわかっているとき,原因の先験的な確率(事前確率)が与えられたら,結果が知られた後での原因の確率(事後確率)が計算できるという立場をとっている。この立場の理解については,後世まで議論されるところとなった。…
※「ベイズの定理」について言及している用語解説の一部を掲載しています。
出典|株式会社平凡社「世界大百科事典(旧版)」
Sponserd by 
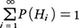 だから,確率の計算,
だから,確率の計算,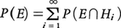 により,
により,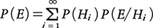 を得る。
を得る。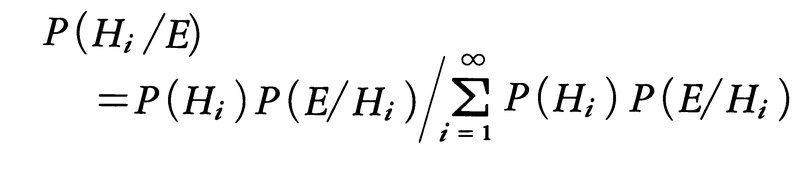
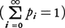 。いまそれが男子ばかりの家庭であることがわかったとき(これを事象Eとする),ひとりっ子の家庭(すなわちH1)である確率P(H1/E)を求めよう。一般に男女の出生率に違いがないとしてよいとすれば,i人の子どもがあって全部男子という確率は1/2iと考えられる。すなわちP(E/Hi)=1/2i。よってベイズの定理から,ひとりっ子である事後確率は,
。いまそれが男子ばかりの家庭であることがわかったとき(これを事象Eとする),ひとりっ子の家庭(すなわちH1)である確率P(H1/E)を求めよう。一般に男女の出生率に違いがないとしてよいとすれば,i人の子どもがあって全部男子という確率は1/2iと考えられる。すなわちP(E/Hi)=1/2i。よってベイズの定理から,ひとりっ子である事後確率は,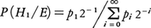 である。ところが,このベイズの定理に対して,形而上学的な見地から,機械的に応用することに強い批判がある。事前に情報がないときは,起こりうるいくつかの可能性はすべて同程度に確からしいとすることに問題があるからである。これまで5000年の間,毎日太陽は東から昇った。明日も東から昇る確率はいかにといった例を考えたらその理由が推察される。具体的な問題に応用するときには注意が必要である。
である。ところが,このベイズの定理に対して,形而上学的な見地から,機械的に応用することに強い批判がある。事前に情報がないときは,起こりうるいくつかの可能性はすべて同程度に確からしいとすることに問題があるからである。これまで5000年の間,毎日太陽は東から昇った。明日も東から昇る確率はいかにといった例を考えたらその理由が推察される。具体的な問題に応用するときには注意が必要である。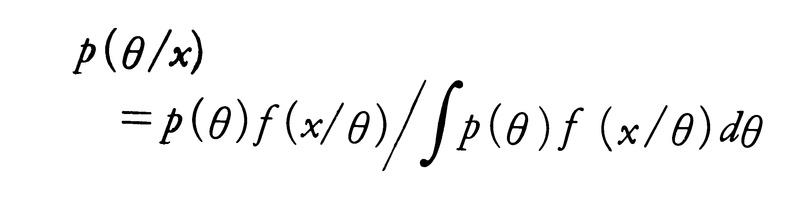


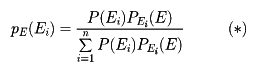
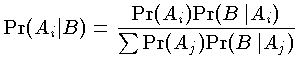 結果から原因の確率を逆算することができる点が興味深く,応用例もきわめて多い。証明は,条件つき確率そのものであって,まったく容易であるが,上記のように,深い哲学上の因果律を負わせることに反対する意見もある。 T.ベイズ (1702~61) はイギリスの牧師である。逆確率の定理ともいわれる。
結果から原因の確率を逆算することができる点が興味深く,応用例もきわめて多い。証明は,条件つき確率そのものであって,まったく容易であるが,上記のように,深い哲学上の因果律を負わせることに反対する意見もある。 T.ベイズ (1702~61) はイギリスの牧師である。逆確率の定理ともいわれる。
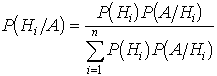 が得られる。これがいわゆる
が得られる。これがいわゆる