クラインの壺（読み）クラインノツボ

デジタル大辞泉

クライン‐の‐つぼ【クラインの^×壺】

二つのメビウスの帯を境界線に沿ってはり合わせるとできる、境界がなく表裏の区別もない閉曲面。三次元空間では実現せず、模型図によって示される。ドイツの数学者フェリックス＝クラインによって考案された。クラインの管。クラインの瓶。

出典　小学館

日本大百科全書(ニッポニカ)

クラインの壺
くらいんのつぼ

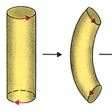
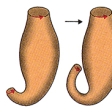
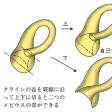
円柱の上下の境界の二つの円周に図Aの矢印で示したような向きをつけておく。この向きが相反するように二つの円周をあわせると、輪環面（トーラス）ができる。ここで、この向きが一致するようにあわせると、円柱は自身を横切ることになり、図Bのような円周で自己交差する図形ができる。しかし、この図形を四次元空間中に入れて図形の一部分を四次元方向へずらすと、この自己交差をなくすことができ、この閉曲面が、フェリックス・クラインによって発見されたクラインの壺である。クラインの壺は図Cのように2等分すると、それぞれがメビウスの帯となるので、二つのメビウスの帯を境界に沿って貼(は)り合わせてもできる。クラインの壺は不可符号の閉曲面の重要な例であり、輪環面とは位相的性質が本質的に異なる。

［野口　廣］

[参照項目] | メビウスの帯

クラインの壺（輪環面〈トーラス〉）〔図…

クラインの壺（円周で自己交差する図形）…

クラインの壺（クラインの壺とメビウスの…

出典　小学館　日本大百科全書(ニッポニカ)

ブリタニカ国際大百科事典 小項目事典

クラインの壺
クラインのつぼ
Klein bottle

クラインの瓶ともいう。メビウスの帯と同じように，表と裏の区別がつかない面である (→メビウスの曲面 ) 。このような面を不可符号な曲面とか，向きのつけられない曲面とかいう。クラインの壺をつくるには，まず長方形 ABCD (薄いゴム板のようなものを想像する) の，AとB，CとDを重ねて，AD，BCを貼合せて円管をつくる。次にこうしてできた円管を1回ねじって，AとC，BとDを重ねて，AB，CDを貼りつければよい。これは3次元ユークリッド空間内では実現できないが，普通は図のように，円管の一方の口を曲面にもぐりこませ，内側からもう一方の口に接続させてできる面として示される。

出典　ブリタニカ国際大百科事典 小項目事典

デジタル大辞泉プラス

クラインの壺

①岡嶋二人の長編ミステリー。1989年刊行。ヴァーチャルリアリティ・システム「クライン2」の制作に関わることになった主人公が、虚構と現実の狭間に落ち込んでいく。
②①を原作とする日本のテレビドラマ。放映はNHK教育（1996年3月）。全10回。脚本：井上夢人ほか。主題歌：Panache。出演：国分博、嶋田久作、中山忍ほか。

出典　小学館