スペクトル分析（読み）スペクトルブンセキ（英語表記）spectral analysis

デジタル大辞泉

スペクトル‐ぶんせき【スペクトル分析】

分光分析。

出典　小学館

精選版 日本国語大辞典

スペクトル‐ぶんせき【スペクトル分析】

1. 〘 名詞 〙 物質の粉末を高温の炎に入れ、その発光するスペクトルから含まれている元素の分析をする方法。分光分析。発光分析。

出典　精選版 日本国語大辞典

日本大百科全書(ニッポニカ)

スペクトル分析
すぺくとるぶんせき
spectral analysis

時系列データのもつ循環的要素の強さを分析し、データ変動の背後にある周期性を明らかにする解析方法。スペクトラル解析ともよばれる。

　いま、x₁、x₂、……という時系列データがあるとする。これらはXというある対象（たとえばあるデパートの売上高やある会社の株価など）の、それぞれの時点で観測したときの数値であるが、これらは各時点で確率的に変動するそれぞれの変数（確率変数）の一つの実現値であると考える。このように考えたとき、観測された時系列データの背後にある確率変数の列x₁、x₂、……は確率過程とよばれる。この確率変数列からk時点置きにとった確率変数の組合せ(X₁,X_1+k),(X₂,X_2+k),……についての共分散（自己共分散関数）はすべてkだけに依存する値となるものとし、γ_kとする。また、それぞれの確率変数の期待値は、すべて同じであるとする。このような性質をもつ確率変数列のことを定常的確率過程とよんでいる。

　そうすると、自己共分散関数γ_kの周期性は、もとの確率過程のもつ周期性をそのまま保持することが数学的に示される。このことに着目すると、時系列データがどのような循環的特性をもつかは、その背後にあると想定される確率過程の自己共分散関数γ_kによって検出することができるわけである。そのために、次の式で与えられるスペクトル密度関数spectral density functionが用いられる（密度関数としては、一般にはγ_kのかわりに、それをγ₀で除して正規化したものが用いられる）。

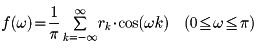
　この式によると、γ_kの周期運動がcos(ωk)のそれに一致した場合にf(ω)の値は最大となり、一致しない場合には、異なったkに対するγ_k・cos(ωk)の値が互いに打ち消し合うことによって関数の値は小さくなる。すなわち、種々のωの値について関数f(ω)の値を計算し、その値がもっとも大きくなるようなωをみいだせば、γ_k、したがってもとの時系列自体が、振動数ω/2π（あるいは、周期2π/ω）の主要循環運動を含むものであることが判明することになる。

　このような分析方法は、1940年代なかば以降、アメリカを中心に確率過程に関する理論的研究の一環として進められてきたが、1950年代に入り、コンピュータが利用可能となるにつれて、とくに1960年代以降は実際の時系列データについての実証研究に広く応用されるようになった。そして、この手法はとくに経済データの季節変動の分析や景気循環の研究などに、理論的改良が加えられつつ現在も一つの有力な分析用具として応用されている。

［高島　忠］

[参照項目] | 時系列分析

出典　小学館　日本大百科全書(ニッポニカ)

世界大百科事典（旧版）内のスペクトル分析の言及

【音声情報処理】より

…人間の耳は，波形に含まれる強い周波数成分を抽出している。これを周波数分析とかスペクトル分析という。人間の音声は時間的に変化するので，短い時間区間(通常は，0.005～0.02秒)ごとにスペクトル分析を行う。…

※「スペクトル分析」について言及している用語解説の一部を掲載しています。

出典｜株式会社平凡社「世界大百科事典（旧版）」