ゼロ（英語表記）zero

精選版 日本国語大辞典

ゼロ

1. 〘 名詞 〙 ( [ラテン語] zelo ) キリシタン用語。熱愛。熱心。渇望。
   1. [初出の実例]「ワガ ヒデス ト、モエタツ zelo(ゼロ) ヲ」(出典：サントスの御作業の内抜書（1591）二)

出典　精選版 日本国語大辞典

改訂新版　世界大百科事典

ゼロ
zero

零ともいう。任意の実数xに対しx＋0＝xとなるただ一つの実数。203400という数字の中の0の役割を考えてみよう。この二十万三千四百という数を表すのに，0，2，3，4のみを使っている。一般に0，1，……，9という10個の数字ですべての数を書き記すことができる。そのためには，位取りの原則が不可欠である。すなわち，数字の位置でその桁を示すことにより，十，百，千，万，……が不必要になる。しかし，ある桁に数がないことを意味する記号がいるが，それが0の役割である。例えば，203400では各0が一，十，万の桁に数がないことを示している。それでは位取りの原則と，それを有効にする0は，どこで，いつごろ発見されたのであろうか。これにはいろいろな説があり，決定的な証拠はない。位取りの原則は古くから利用されていた。よく知られているのはメソポタミアで，前2000年ころには使われていたとされている。ゼロはで表され，これも前400年には存在していた。しかし，ゼロの使用にはあいまいなところがあり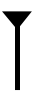，で，2×（60²）＋0×60＋1も2×（60³）＋0×（60²）＋60も意味した。数の最後にはを使わなかったのである。200年ころにはこのようなあいまいさをなくした記法も利用されるようになったが，それは天文学などの特別の分野のみで一般的ではなかった。

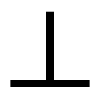
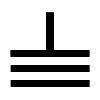
　別の例として中国の算木がある。中国では前数百年ころから算木を使って数を表し計算をした。一の桁では棒を縦に置いて1を，横に置いて5を表し，十の桁では横棒が1，縦棒が5を表した。以下，桁が変わるごとに縦横を逆にしていく。例えば，は56789。もし数のない桁があると，そこには算木を置かなかった。算木と同じ考え方は，そろばん，計算盤でも用いられてきた。そろばんでは位取りの原則を利用しているが，数のない桁はたまを動かさないことで示す。また，テーブルや板の上に石を置いたり，数字を表す記号を書き並べて計算するのに使った計算盤でも，ある桁に数がなければ，そこをあけておいた。

　このように位取りの原則は広く利用されていたが，それを抽象して，ふつうに使う数字の体系の中に組み込み，0を使いこなし，それを使っての計算法の確立を成し遂げたのはインド人である。この点では諸説が一致している。さらに，インド人は0を位取りの原則を有効にするための記号としてのみでなく，1，2，……と同等な数であると認識していた。ギリシアにも〈無〉という概念はあったが，これを数とは理解しなかった。インドのブラフマグプタ（7世紀）は負の数とともに0の計算法則をも扱ったとされる。ただ，彼は0÷0＝0とし，a÷0については何もいっていない。後にバースカラ2世はa÷0（a≠0）は無限大であるといっている。

　インドでの0の発見はいつごろ，どのようにしてなされたのであろう。これにも種々の説がある。確実な資料は中央インドのグバリアーにある小寺院の壁に彫られたものである。870年のもので，その中に270と50という数字が現れ，ゼロが小さな円で記されている。先に述べたようにブラフマグプタが7世紀に0の計算を扱っていることから，インドでの0の使用は7世紀まではさかのぼりうる。最初のうちは0でなく ・ などの記号が使われていた。インドでのゼロの発見と他の文化圏との関係についても種々の議論がある。メソポタミア，バビロニアからの刺激，ギリシアからの輸入，位取りの原則への中国の算木の影響などがいわれるが，どれにもはっきりとした証拠はない。インドにおける文献が極端に少ないこともあって，これらの議論に結着をつけることはむずかしいであろう。インドでは板の上に砂をまいて，そこに数字を書いて計算をし，結果のみをことばで記した。砂の上に書かれた数字，計算は消えて資料としては残らない。他の文化圏からの影響の例として，ゼロの形0がギリシア文字のο（オミクロン）からきたのではというのがある。οはギリシア語で〈空〉を意味するoudenの頭文字である。実際，プトレマイオスは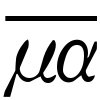ο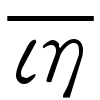で41度0分18秒を表している。しかし，記号0とοに関係があるとする説は疑わしいとする人が多い。

　マヤ文明でも位取りの原則と数のない桁を示す記号ゼロとが利用されていた。マヤの記数法は暦と深い関係があり，日常的にこの記数法が使われていたかどうかわからない。また，他の文化圏との交流もはっきりしないので，マヤ文明のゼロがマヤの独創であるかどうかも定かではない。

　さて，インドで確立した記数法はゼロも含めて9世紀にアラビアに伝えられた。そのころフワーリズミーは〈ヒンドゥー式計算法〉についての本を著した。これは多分ブラフマグプタの本をもとにしたものと思われる。この本ではインド式記数法に基づいた計算法が紹介されている。今日われわれがインドの数字のことをアラビア数字といっているのは，この本などのため，アラビア人がこの記数法を考えだしたと誤解されたからである。サンスクリットではゼロのことをśūnya（空白のこと）と呼んだが，これがアラビア語に訳され，そのアラビア語の音がヨーロッパに入って，ラテン語でcifra，あるいはzephirumと書かれた。2番目の形がイタリアでzefiro，zefro，zeveroと書かれるようになり，これがベネチアの方言でzeroとなったとされる。インドの数字は10世紀に当時アラビア文化圏であったスペインを通してヨーロッパに導入されたが，ゼロの意味も重要性も理解されず，ただ1から9までの数字のみが計算盤で利用された。13世紀のヨーロッパでインドの記数法，計算法を（ゼロも含めて）大衆化する努力がはらわれた。フィボナッチはエジプト，シリア，ギリシアなどを旅行した後，1202年にインドの記数法，計算法の本を書いた。パリ大学のサクロボスコも1240年に同様の本を著した。このようにして0はヨーロッパに入ったが，インドの記数法と計算法が，ともに日常化したのは，15世紀以降のことである。
→記数法　→数字
執筆者：丸山 正樹

出典　株式会社平凡社「改訂新版　世界大百科事典」

日本大百科全書(ニッポニカ)

ゼロ
ぜろ
zero

何も存在しないことを表す数0のこと。日本語では零という。0は整数である。0は、もともと位取り記数法で、ある位が欠けていること、つまり、空位を表す記号としてインドで非常に古い時代に発見され（一説には紀元5～6世紀）、その後、数として取り扱われるようになったという。十進位取り記数法(じっしんくらいどりきすうほう)では1234と書けば、千二百三十四を表し、1、2、3、4の数字はその置かれている位置によって、違った大きさを表している。つまり、最初の1は千の位が1であること（1000）、次の2は百の位が2であること（200）、3は十の位が3であること（30）、4は一の位が4であること（4）を表している。この位取り記数法で、たとえば、百の位が欠けていることを表すのに、1 34と空位をあけておくだけにすると、最初の1がなんの位かはっきりせず、誤るおそれがある。そこで、空位をはっきりと表す記号として0を考え、それを使うことにすると、1034のように紛れがなくなる。このように、位取り記数法には空位を表す0が必要不可欠である。十進位取り記数法では、1、2、……、9、と0の10個の数字を使って、どんな整数も小数も表すことができる。

　簡潔で明らかな表し方である位取り記数法は、ほかにどんな利点があるかといえば、それはまず第一に、上の桁(けた)へ移っても新しい記号が不要であること。たとえば、漢数字では、百、千、万、億、兆、またローマ数字では、X(10),C(100),M(1000)のように、位取りでない記数法は次々と新しい数字が必要となるのに、位取り記数法では必要としない。第二は、表された数の大小をひと目で知ることができること。第三の、そしてもっとも重要なのは、計算が容易になることである。位取りでない記数法で表された数について、加減の計算はそれほどでもないにしても、乗除になると複雑になり、手に負えなくなる。たとえば、中世ヨーロッパでは計算は計算親方といわれる人の仕事であったし、日本では計算はそろばんに任されていたのである。ところが位取り記数法で表された数では、計算の仕方がわかりやすく、だれにでも理解できるものとなった。0を用いた位取り記数法は、インドからアラビアを経てヨーロッパに伝わったので、アラビア数字の名が残っている。

　数としての0は次の性質がある。加法において、どんな数aについても、a+0=0+a=aとなる。減法ではa-a=0,a-0=aとなる。乗法においては、どんな数についてもa×0=0×a=0となる。除法では0でない数aについて0÷a=0となるが、0で割ることはできない。数の範囲を負の数まで広げると、0は正の数と負の数の境目にあたる数で、どの正の数よりも小さく、また、どの負の数よりも大きい数である。

［三輪辰郎］

『吉田洋一著『零の発見』（岩波新書）』

[参照項目] | 数

出典　小学館　日本大百科全書(ニッポニカ)

現代外国人名録2016

ゼロ
Zelo

職業・肩書

歌手

国籍

韓国

生年月日

1996年10月15日

グループ名

グループ名=B.A.P(ビーエーピー)

経歴

2012年ヨングク、ヒムチャン、デヒョン、ヨンジェ、ジョンアプとともに男性6人組グループB.A.Pを結成、ラップとダンス、ビートボックス、アクロバットを担当。B.A.Pとは、“Best(最高の)Absolute(絶対的な)Perfect(完璧な)価値を追求する”という意味。シングル「Warrior」でデビューし、ヒップホップ中心の音楽と完成度の高いダンスパフォーマンスで韓国の新人賞を総なめにしたほか、ドイツや中国でも新人賞を獲得。2013年にはニューヨーク、ワシントンなど米国4都市のほかシンガポール、香港などの世界ツアーを行う。同年秋日本デビューを果たす。

出典　日外アソシエーツ「現代外国人名録2016」

ブリタニカ国際大百科事典 小項目事典

ゼロ
zero

零。アラビア数字の一つ。数字0で表わされる数。空集合の集合数，すなわち無を表わす。数0は，自然数 (0を自然数に含める流儀もある) ，負の整数とともに整数に含まれる数であって，数学的には次のように定義される。いかなる数 a に対しても a＋x＝x＋a＝a なる数 x を0と書く。0のこの定義と分配の法則から a×0＝0×a＝0 なる性質が導かれる。また指数関数においては a⁰＝1 と定義される。ただし，0を除数とする除法は定義されない。0は古代インドにおいて発見され，アラビアを経由してヨーロッパにもたらされた。数字0がもたらした数の表記法における簡便さと，数0という数学的な概念の重要さから，ゼロの発見は文化史上に重要な意義をもつ。

出典　ブリタニカ国際大百科事典 小項目事典

日本の企業がわかる事典2014-2015

ゼロ

正式社名「株式会社ゼロ」。英文社名「ZERO CO., LTD.」。陸運業。昭和36年(1961)「日産陸送株式会社」設立。平成13年(2001)現在の社名に変更。本社は川崎市幸区堀川町。車両輸送会社。主力は日産自動車の新車輸送。ほかに輸入車・中古車など。中古車オークションの運営や家電など一般貨物輸送も手がける。東京証券取引所第2部上場。証券コード9028。

出典　講談社

百科事典マイペディア

ゼロ

零(れい)とも。任意の実数xに対しx＋０＝xとなるただ一つの実数。０は前２世紀ごろインドで，まず位取りを示す記号として導入され，次いで数としての０が考えられ，アラビア数字に導入された。任意の数と０の積は０。０で割ることは不可能。

出典　株式会社平凡社

デジタル大辞泉プラス

ゼロ〔曲名〕

日本のポピュラー音楽。歌は日本のバンド、BUMP OF CHICKEN。2011年発売。作詞・作曲：藤原基央。スクウェア・エニックスのゲームソフト「ファイナルファンタジー零式」のテーマソングに起用。

ゼロ〔菓子〕

株式会社ロッテが販売するチョコレートの商品名。糖類不使用。パフ入りの「クリスプ」もある。

出典　小学館

世界大百科事典（旧版）内のゼロの言及

【インド数学】より

…8種の実用算とは，混合，数列，平面図形，堀，積重ね，鋸，堆積物，影に関するものである。また同書第18章〈クッタカ〉では，ゼロ，負数，無理数などの演算規則のほか，一元一次，一元二次の方程式や多元連立方程式，また二元一次，二元二次の不定方程式などが扱われる。この二つの章で扱われた内容がそれぞれ，これよりやや遅れておそらく8世紀ころ，狭義のガニタの二大分野パーティー(語源は〈書板〉を意味するパッタないしパタか？)およびビージャガニタ(種子数学)へ発展する。…

【記数法】より

…　位取りの原則を利用した記数法は4000年ほど昔からメソポタミアで発達した。この場合，ある桁に数字がないことを意味する記号，すなわちゼロが必要になる。メソポタミアでは前4世紀までにゼロを表す記号としてが使われるようになった。…

【数】より

…〈かず〉ともいう。数学で単に数という場合，複素数を意味するが，もっと狭く，実数に限定した意味に用いられることもよくある。おおまかに分類すれば次のようになる。また代数的数の概念に関連して次の分類もある。また実数の分類には次の二つもある。
［数概念の発達］
　数概念の出発は，個数を数えることから自然数の概念に到達することであり，いろいろな古代文明において，その段階には到達していた。次の段階は正の分数であるが，この発展については地域による差が大きかった。…

※「ゼロ」について言及している用語解説の一部を掲載しています。

出典｜株式会社平凡社「世界大百科事典（旧版）」