デバイの比熱式 (デバイのひねつしき)
Debye's specific heat formula
固体の比熱について,アインシュタインの比熱式の改良としてP.デバイが1912年に提案した式。アインシュタインは,固体内の個々の格子点を独立な単振子として扱ったが,デバイは格子の集団運動の本質をとり入れて,まず固体を連続弾性体とみなした。連続体では運動の自由度が無限大になるが,格子では有限であることを考慮して,連続体の振動モードのエネルギーの低いほうからとり入れ,モードの数が格子点の自由度と等しくなるところで打ち切る。このようにして求められた定積モル比熱は,
Cv=3RfD(ΘD/T)
と書かれる。Rは気体定数,Tは絶対温度,ΘDは上の打切りに対応するエネルギーでデバイ温度と呼ばれ,数百Kの程度である。また,fDはデバイ関数と呼ばれ,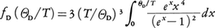 である。デバイの比熱式では,Cvは低温でT3に比例,また高温では一定となってデュロン=プティの法則に一致し,広い温度域にわたってよく実験と整合する。
である。デバイの比熱式では,Cvは低温でT3に比例,また高温では一定となってデュロン=プティの法則に一致し,広い温度域にわたってよく実験と整合する。
執筆者:小林 俊一
出典 株式会社平凡社「改訂新版 世界大百科事典」改訂新版 世界大百科事典について 情報
Sponserd by 
法則の辞典
「デバイの比熱式」の解説
デバイの比熱式【Debye's formula of specific heat】
高温ではデュロン‐ブティの法則*,低温ではデバイの T3 法則*をともに満足させられるように考えられた比熱の方程式.3N 個の結合した振動子のエネルギーを量子力学的に計算した結果導かれた,固体の定積比熱(Cv)の温度依存性を表した式である.
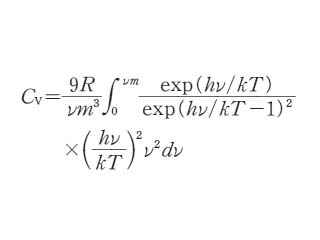
ここで νm はデバイ周波数と呼ばれる.3N 個の振動のうち最大のものの値に相当するが,物質によって異なる.hν/k は温度の次元をもつ量で,デバイ温度*と呼ばれ,Θ(ときには Θc)で表すことが多い.Θ/T は無次元数であるが,これを x とおいたときには
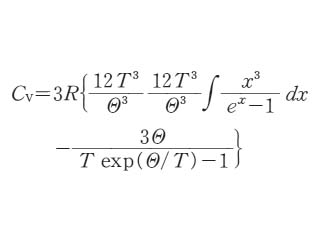
となる.
出典 朝倉書店法則の辞典について 情報
Sponserd by 
デバイの比熱式
デバイのひねつしき
Debye's specific heat formula
出典 ブリタニカ国際大百科事典 小項目事典ブリタニカ国際大百科事典 小項目事典について 情報
Sponserd by 
世界大百科事典(旧版)内のデバイの比熱式の言及
【比熱】より
…アルゴンなどの単原子気体では定積モル比熱Cvは3/2R,水素,酸素などの2原子気体ではCv=5/2R,多原子気体ではCv=3Rに近い。 固体の比熱に関しては,その定積モル比熱Cvが3Rに等しいという[デュロン=プティの法則]や,アインシュタインによる[アインシュタインの比熱式],これを改良したデバイによる[デバイの比熱式]がある。デバイの比熱式は,格子振動を連続体の弾性振動(縦波と二つの横波)でおきかえることによって導かれたもので,絶対温度をTとして,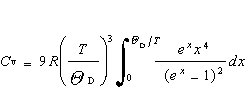 と表される。…
と表される。…
※「デバイの比熱式」について言及している用語解説の一部を掲載しています。
出典|株式会社平凡社「世界大百科事典(旧版)」
Sponserd by 
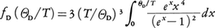 である。デバイの比熱式では,Cvは低温でT3に比例,また高温では一定となってデュロン=プティの法則に一致し,広い温度域にわたってよく実験と整合する。
である。デバイの比熱式では,Cvは低温でT3に比例,また高温では一定となってデュロン=プティの法則に一致し,広い温度域にわたってよく実験と整合する。

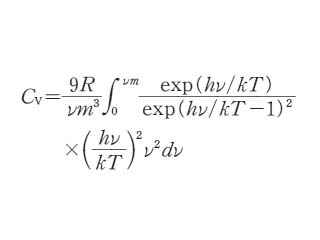
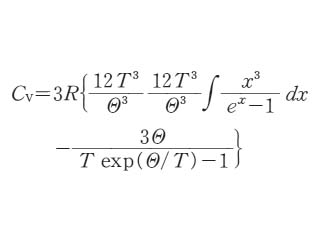
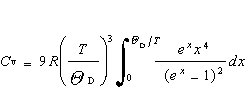 と表される。…
と表される。…