目次 比例式の性質 比例定数 建築における比例 四つの数a ,b ,c ,d について,a :b =c :d であるとき,a ,b ,c ,d は比例をなしているといい,a :b =c :d を比例式,または比例という。a ,d を比例式の外項,b ,c を内項と呼ぶ。また,三つの数a ,b ,c について,a :b =b :c であるとき,b はa ,c の比例中項であるという。
比例式の性質 四つの数a ,b ,c ,d について,
(1)a :b =b :c ならば,ad =bc 。すなわち,比例式の外項の積は内項の積に等しい。
(2)逆に,ad =bc (≠0)ならば,a :b =b :c である。
(3)したがって,a :b =c :d (ad ≠0)ならば,a :c =b :d ,d :b =c :a ,b :a =d :c 。すなわち,比例式が与えられたとき,その内項を交換してもよいし,外項を交換してもよい。
(4)a :b =b :c (ad ≠0)のとき,次の(a)~(c)が成り立つ。
比例定数 変化する二つの数(または量)x ,y と,一定の数(または量)k があって,y =k ・x となるとき,y はx に比例する(あるいは正比例)といい,k を比例定数という。このとき,x が2倍,3倍,……になれば,それに対応するy も2倍,3倍,……になる。このx ,y のグラフ は原点を通る直線になり,その直線の傾きは比例定数k によって決まる。反比例 西村 純一
建築における比例 建築家が建物を構想していくうえで,各部寸法やそれと全体との関係,すなわち比例を考えるのは,欠くことのできない過程であり,比例の決定方法は建築家にとって古くから重大な関心事であった。古代には,人々の宇宙観とかかわる数値が用いられることが多く,たとえば,旧約聖書 に記されたソロモン の神殿では,2と3を組み合わせた数値によりすべての寸法が決定されていたが,これらの数は,太陽と月,あるいは天と地,当時知られていた惑星の数などと関連しているとみられる。またエジプト などでは,建築の配置や立面の決定にあたって,こうした数値を基にした〈基準格子〉が用いられていたことも知られている。宇宙観とのさらに直接的なかかわり方としては,ピラミッド斜面の角度が星の位置との関係で定められたとか,ジッグラトの階段高さが,ある惑星の見かけの往復運動を象徴しているといった例も見られる。
これら抽象的・象徴的比例観に対し,古代ギリシア人は比例を形態美の源泉とみなし,生物的形態,とりわけ人体が,もっともよく宇宙的調和を体現した比例をもつものとして,それを建築にあてはめた。円柱はそのまま人体になぞらえられ,たとえばドリス式円柱は男性の人体であり,その高さは直径の6倍とするのが望ましく,イオニア式 は女性で,直径の8倍の高さがよいとされた。そして円柱直径の1/2を1モデュール と呼び,各部寸法をすべてこれの倍数値で表す方式が,いわゆる〈オーダー 〉の体系の根幹となっていた。古典建築の最初の理論家,古代ローマのウィトルウィウス は,こうした比例の体系こそが建築を科学たらしめるものであると信じていたが,同時に,ピタゴラス やプラトン を引用しながら,6という数の神秘性を強調しており,比例の観念と神秘主義 ,象徴主義との結びつきの深さをおもわせる。
中世には古代ギリシアの美的,功利的な比例観は薄れ,代わってキリスト教的な象徴主義が主流となり,三位一体 を表す3や十二使徒を表す12などの数値を用いた単純な倍数系列が多く見られた。しかし12世紀以降は,ピタゴラス派の協和音程理論の比例数値により平面を決定した教会堂が現れており,これはノートル・ダム楽派 の荘重な〈オルガノン 〉の出現と軌を一にしている。同様に,華麗なフランボアイヤン・ゴシックと複雑精緻なリズムで構成される〈アルス・ノバ 〉の音楽の出現も,密接な関連をもっている。中世の音楽と建築は,古典古代の人体寸法を基にした比例とは異質の,きわめて人工的で超越的な比例秩序を共通の基盤にしていたといえる。
ルネサンス に入ると,再びウィトルウィウスを基礎とする比例理論が建築の中心課題となり,ここでもまたピタゴラスの理論が重要な手がかりとされたが,しかし人体的比例の堅持と,それに加えて透視図法的な,一定の視点からの三次元的比例が主たる関心事となった。L.B.アルベルティ,フランチェスコ・ディ・ジョルジョ・マルティーニ ,レオナルド・ダ・ビンチといった当時の代表的比例理論家たちは,音楽用語を用いて建築の比例を論じ,調和級数によって空間の奥行き の比例を決定しようとしていた。16世紀以降は,さらに新プラトン主義 の影響による数の神秘主義が加わり,きわめて知的な古典主義的比例の体系が確立されていく。A.パラディオの《建築四書》に示された建物寸法は,すべてこうしたルネサンス的な比例によって与えられたものであった。しかしこの間,16世紀のマニエリスム の到来とともに,こうした静的な比例観に対しては批判が加えられるようになり,ミケランジェロにあっては,比例はもはや不変の美の規範ではなく,作家個人の手法に属するものとみなされるようになっていた。バロック ,ロココ を通じてこの傾向はさらに強まり,18世紀の新古典主義においても,一部でフリーメーソン により象徴的比例の復活がみられたものの,ロマンティックな超越的壮大さや不規則な美を求める傾向に押され,再び建築理論の中心的位置を占めるには至らず,近代の合理主義 は,宇宙観とのアナロジー による古典的な比例の伝統を完全に絶ち切ってしまう。
19世紀の建築理論家ビオレ・ル・デュクは,比例よりも尺度の重要性を説き,ある尺度に基づく基準格子(二等辺三角形)の使用を推奨している。一方,19世紀から20世紀初めにかけては,純粋な視覚上の問題として比例に関心が寄せられ,パルテノンなどの建築の美を,その比例やいわゆる視覚矯正などから解き明かそうとする試みが盛んとなり,その結果を制作にも反映させようとする動きがみられた。また近代の工業化は,尺度に対する新しい要求(モデュラー・コーディネーション)を提起しており,その手段としての〈モデュール〉設定が望まれるようになった。ル・コルビュジエ のモデュロール は,こうした二つの要求を同時に満たそうとしたもので,人体寸法を基準とし,フィボナッチ数列を駆使した複雑な体系からなっている。しかしこれはル・コルビュジエの期待に反し,彼の一門の人々以外からはほとんど用いられることがなかった。そのあまりの複雑さにもよるが,本来的にアナロジカルな象徴性を有する比例概念と,純実用的な尺度概念とを直接的に結びつけたことにも,その原因があったと見られる。またその比例の裏付けとなるべき現代の宇宙観・世界観の混乱も,これを助けた。
モデュロール以外の現代のモデュールは,こうした形而上学とまったくかかわらない,純実用的な尺度の体系に甘んじている。しかし,建築の比例に対する内的な要求は決して消滅したわけではなく,古典的な比例理論と比肩しうる新たな比例理論を獲得できるかどうかは,われわれの世界観が何らかの新たな抽象的比例によって表現しうるか否かにかかっているといえよう。オーダー →音律 福田 晴虔



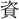 塗(しと)を以て人を用ひ、能否を問はず、比例從事して、是非を
塗(しと)を以て人を用ひ、能否を問はず、比例從事して、是非を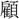 みざるは、此れ最も國家の
みざるは、此れ最も國家の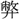 法にして、宜しく革正すべき
法にして、宜しく革正すべき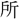 の
の なり。
なり。