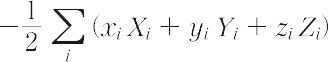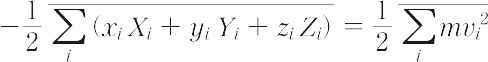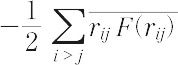改訂新版 世界大百科事典 「ビリアル」の意味・わかりやすい解説
ビリアル
virial
1870年R.クラウジウスによって導入された熱力学（気体分子運動論）上の概念。語源はラテン語の力を意味するvisの複数形であるviresに由来する。気体分子に働く力によってその気体の特徴，とくに状態方程式が理想気体の場合の式pV＝RTからどのようにはずれるかを表す目的で考えられた（pは圧力，Vは体積，Tは絶対温度，Rは気体定数）。気体の分子iに働く力をFi，分子iの位置ベクトルをriとして，スカラー積－1/2Fi・riのすべての分子に関する和の平均，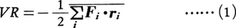
をその気体のビリアルVRと定義する（（1）の右辺の量は位置ベクトルの原点の選び方によらないことに注意）。以下ではこれが気体の状態方程式の決定に重要な役割を果たすことを示す。
1辺の長さLの立方体の容器につめられた気体の呈する圧力pを計算するため，その一つの器壁面（例えばx軸に垂直な面）に対し単位時間・単位体積当りx軸方向にvxなる速度のn個の分子が衝突するとすれば，そのときの運動量変化－2⊿Mxがpに寄与する分は－2⊿Mx・nvxである。これに運動量の変化が力積に等しいことを用いると，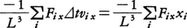
となるから（tは時間を表す），分子運動のすべての方向について平均することにより，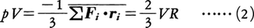
が得られる。このときのVRは壁が分子に及ぼす力のビリアルで，外部ビリアルと呼ばれる。気体分子が互いに独立に運動する理想気体では，分子の運動エネルギーをKとするとpV＝2/3×＝RTだから，VR＝という関係になる。重要なことは，分子間力が無視できない不完全気体に対してもこの関係が成り立ち，このことを用いて不完全気体の状態方程式を見いだす手段が得られることである。ただし，この場合のVRは外部ビリアルVRoのほかに分子間力による内部ビリアルVRinの寄与があるので，これを計算によって与える必要がある。その結果，一般の状態方程式は，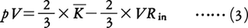
と書かれることになる。ここで￣で示される平均の意味は，統計力学で用いられる分子集団の熱平衡分布についての平均であり，分子の模型が古典力学であるか量子力学であるかに従ってそれぞれ適切な分布を用いなければならない。十分希薄な気体で古典統計力学の分布（ボルツマン分布）でよい場合，（3）の右辺第1項はエネルギー等分配の法則によりRTに等しいので，右辺第2項，すなわち内部ビリアルが理想気体の状態方程式からのずれを表す唯一の部分となる（量子気体では自体温度Tの複雑な関数として等分配則からのずれを示す）。分子間力が，2分子対の距離だけの関数で与えられるポテンシャルの和，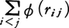
から導かれる場合，内部ビリアルは，
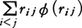で与えられることは容易にわかる。
ビリアル定理
上述のように，関係式（3）は不完全気体の状態方程式の意義をもつものであるが，その根拠を与えるのがビリアル定理であって，
VRin＋VRo＝
のように表される。これを，N個の分子の2f＝6N次元相空間における分子系のハミルトニアンH（p，q）が，pjの一般の二次形式の運動エネルギーKとqjだけの関数であるポテンシャルエネルギーUの和で表される標準的な場合について導こう。Uは分子間力を与える相互作用のポテンシャルと分子系に対する容器壁からの作用（これも通常ポテンシャルで表される）との和として表されるので，その双方を合計した（1）の形のVRに対し，VR＝となるというのがこの定理の主張である。分子系の運動は，上述ハミルトニアンH（p，q）により，正準運動方程式，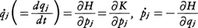
で与えられているので，これを用いて，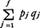
の時間変化を考察すると，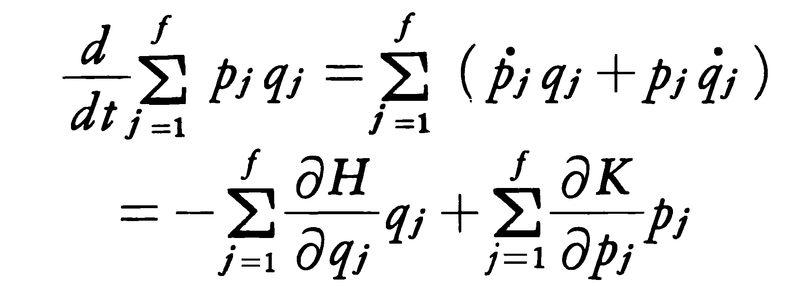
となる。この右辺第1項は，－\(\frac{∂H}{∂qj}\)が一般化座標qjに対する力の成分であることを考慮すると，（1）で定義したビリアルの－2倍であり，また第2項はKが｛pj｝の二次形式であることから2Kに等しい。したがって，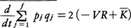
という関係が得られるので，もしこの式の左辺が0ならば，定理の主張であるVR＝が結論されることになる。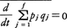
の正しいことは以下のように説明されている。すなわち，ここでいう平均とは分子集団の熱平衡分布に関するものであるが，通常それはエネルギーE＝一定の中での軌道の集団平均とEのボルツマン因子e⁻E/ktを重みとする積分とに分けて行うことができ（kはボルツマン定数），前者の平均はエルゴード仮説のもとに軌道に沿う長時間平均，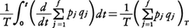
で評価されることを用い，また軌道が有限の大きさの容器内に閉じ込められていることから，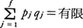
であって，T→∞とともに，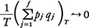
となるからである。
ビリアル展開
古典統計に従う不完全気体の状態方程式（3）を実際に求めるには分子間ポテンシャルに関する分配関数を計算する必要がある。これに対し次のような展開式，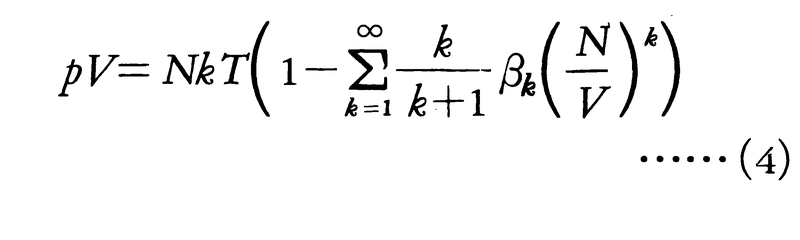
が導かれており，状態方程式のビリアル展開と呼ばれる。この展開式の第1項NkTは理想気体に対応（Nをアボガドロ数としてNk＝R）し，以下の級数は気体の密度\(\frac{N}{V}\)に関するべき級数で表された内部ビリアルである。その第k項の係数βkはk＋1個の分子がクラスターを作った状態からの寄与でk次のビリアル係数と呼ばれている。
執筆者：長谷川 洋
出典 株式会社平凡社「改訂新版 世界大百科事典」改訂新版 世界大百科事典について 情報
