日本大百科全書(ニッポニカ) の解説
マクスウェル‐ボルツマン統計
まくすうぇるぼるつまんとうけい
Maxwell-Boltzmann statistics
多数の粒子の運動を統計的に扱って、その系の性質を表現する方法の一つ。古典力学のように、粒子が互いに識別できると仮定した場合をマクスウェル‐ボルツマン統計という。粒子間の相互作用が非常に小さいとみなせるならば、N粒子からなる系は、それぞれの粒子がどの1粒子状態にいるかによって指定できる。この場合に、系が絶対温度Tの熱浴(物体と接触して熱のやりとりをする外界)に接しているとして統計力学的に扱うと、一つの粒子がj番目の状態(エネルギーεj)をとる確率は
exp[-εj/kT]
に比例することが導かれる。kはボルツマン定数である。この式が示すように、エネルギーの高い状態の確率は低いが、温度が高くなるとその確率は増す。フェルミ分布関数やボース分布関数から出発しても、高温または低密度の極限(またはh→0の極限、hはプランク定数)ではこの分布に近づくことが示される。
高温または低密度の気体は真空中を飛び回る膨大な数の分子からできており、それらの速度はさまざまである。のように速度の3成分を座標軸にとった「速度空間」を考えると、各分子の状態はその中の1点で表される。この速度空間には、分子と同数の点が分布することになる。個々の分子は衝突で速度をめまぐるしく変えるが、熱平衡状態ではのような点の分布は定常的で変化しないと考えられる。マクスウェルとボルツマンはこの分布を調べ、絶対温度がTの気体の場合、分布の密度は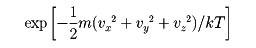
に比例することを導き出した(mは分子の質量)。これをマクスウェル(またはマクスウェル‐ボルツマン)の速度分布則という。上の式のεjのところに、分子の運動エネルギーが入った形になっている。
[小形正男]