一筆書（読み）ひとふでがき

精選版 日本国語大辞典

ひとふで‐がき【一筆書】

1. 〘 名詞 〙
2. ① 初めから終わりまで墨継ぎをしないで、続けて書くこと。また、その書画。いっぴつがき。
   1. [初出の実例]「一筆書きちんころ見たいな顔して居る」(出典：落語・新宿三人遊（1897）〈六代目桂文治〉)
3. ② 一筆ごとに分けて書くこと。箇条書き。ひとつ書き。いっぴつがき。
4. ③ 図形などの書き方の一つ。一度筆を下ろしたら途中で筆を紙から離さず、しかも同じ線を二度以上通らずに書くこと。

出典　精選版 日本国語大辞典

日本大百科全書(ニッポニカ)

一筆書き
ひとふでがき

筆を紙から一度も離さず、おなじ線をなぞらずに、ある図形が描けるかどうか、という問題。この問題は古くからあったが、1736年に数学者オイラーが、今日のトポロジー（位相幾何学）の先駆とみられる二つのテーマを扱った論文を発表した。その一つのテーマが「ケーニヒスベルクの橋の問題」である。これは、ケーニヒスベルク（現、ロシア領カリーニングラード）を流れるプレーゲル川に架かっている七つの橋を、どれも1回ずつ渡って元の場所に戻ることができるかどうかという問題である。オイラーはこの問題の場合にはそうしたコースは絶対に存在しないことを証明した。また同じ論文で、その図（グラフ）のどの頂点でも、その点に出入りしている辺の総数（局所次数という）がすべて偶数であれば、そのグラフは一筆書きできることを証明した。ケーニヒスベルクの場合、それぞれの頂点の局所次数は奇数であり、一筆書きはできない。

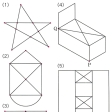
　図の(1)～(3)は一筆書きできるが、図の(4)(5)ではそれぞれ頂点P、Qの局所次数が奇数となり、一筆書きはできない。ただし、元に戻らなくてもよいのであれば、点PかQをそれぞれ書き始め、書き終わりの点にする一筆書きが可能である。二筆書き、三筆書きができる図（グラフ）の研究も行われている。

［野口　廣］

[参照項目] | グラフ理論 | トポロジー

一筆書きの例〔図〕

出典　小学館　日本大百科全書(ニッポニカ)

改訂新版　世界大百科事典

一筆書き (ひとふでがき)

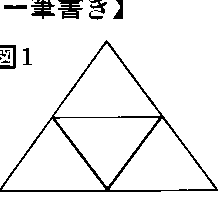
線でできている図形が与えられたとする。このとき，同じ線を2度通ることなく，この図形のすべての線を続けて書いてしまえるならば，この図形は一筆書きできるという。一筆書きできるのはどのような図形であるかという問題は古くから興味をもたれていたが，L.オイラーは1736年にこの問題を次のように解決した。問題となる図形は，いくつかの点と，それらを結ぶ線とで成り立っていると考えられるが，いま，ある点に集まる線の個数が奇数ならばその点を奇点，偶数ならばその点を偶点と呼ぶことにする。すると，奇点の個数はつねに偶数であって，次の原理が成り立つ。（1）例えば図1のように偶点のみからなる図形はどこから始めても一筆書きできる。（2）図2のように奇点が2個だけである図形は，一つの奇点から始めて他の奇点に終わるように一筆書きできる。（3）図3のように奇点の個数が2より多い図形は一筆書きできない。オイラーが一筆書きの問題に興味をもったのは，当時評判のケーニヒスベルクの橋渡りの問題がきっかけであったといわれている。
→位相幾何学
執筆者：中岡 稔

図1～図3

出典　株式会社平凡社「改訂新版　世界大百科事典」

百科事典マイペディア

一筆書き【ひとふでがき】

線でできた図形上のある一点から出発し，連続的に，かつ同じ線の上を２度通ることなしに全部をたどりつくせるとき，この図形は一筆書きできるという。これが可能なための必要十分条件は，集まる線が奇数個の分岐点の数が０または２であること。〈ケーニヒスベルクの橋の問題〉は不可能の例。→位相幾何学
→関連項目グラフ理論

出典　株式会社平凡社

世界大百科事典（旧版）内の一筆書の言及

【位相幾何学】より

…数学では曲面は〈各点の近傍が円板と同相である図形〉と定義されるが，曲面の位相的性質は，その曲面の境界の数，オイラー標数，向き付けの可能性の3条件で決定される。
［一筆書きの問題］
　頂点と呼ばれる有限個の点と，それらを結ぶいくつかの線からなる図形を線状グラフという。線は頂点以外で互いに交わらないものとする。…

※「一筆書」について言及している用語解説の一部を掲載しています。

出典｜株式会社平凡社「世界大百科事典（旧版）」