組合せ理論（読み）くみあわせりろん

日本大百科全書(ニッポニカ)

組合せ理論
くみあわせりろん

与えられた条件を満たす配置の数え上げおよびその構成の問題を取り扱う数学の分野。組合せ理論の始まりは、問題にしている場合の数、または方法の数をもれなく数え上げることであった。確率の理論の初期の発展段階におけるパスカル、フェルマー、ベルヌーイなどの学者の研究は、本質的には組合せの問題に関するものであった。次に、順列・組合せから始めて、典型例をあげる。

［古屋　茂］

順列と組合せ

(1)n個の異なるものからr個取り出し1列に並べたものを、n個のものからr個とった順列という。その総数を_nP_rで表す。

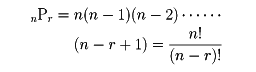
(2)n個の異なるものからr個取り出して得られた集合を、n個のものからr個とった組合せという。その総数を_nC_rで表す。

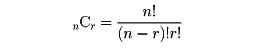
(3)n個の異なるものから繰り返してとることを許してr個取り出して1列に並べたものを、n個のものからr個とった重複順列(じゅうふくじゅんれつ)という。その総数はn^rである。

(4)n個の異なるものから同じものをとってもよいことにしてr個取り出して得られた集合を、n個のものからr個とった重複組合せという。

その総数は_n+r+1C_rである。

［古屋　茂］

n個のものを分ける方法の数

(1)n個の相異なるものをk人に分配する方法（1個も受け取らない人がいてもよいとする）の数はkⁿである。

(2)同じ種類のn個のものをk人に分配する方法（1個も受け取らない人がいてもよいとする）の数は_n+k-1C_nである。

(3)相異なるn個のものをちょうどk個の山に分ける方法の数をS_n^kで表すと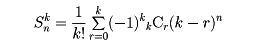

S_n^kを（第2種の）スターリング数という。

(4)同じ種類のn個のものをちょうどk個の山に分ける方法の数は、自然数nをちょうどk個の自然数の和として表す方法の数q_k(n)に等しい。q_k(n)をnとkの関数として簡単な形に表すことはむずかしい。

(5)相異なるn個のものをいくつかの山に分ける方法の数をB_nとすると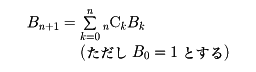

B_nをベル数とよぶ。

(6)同じ種類のn個のものをいくつかの山に分ける方法の数は、自然数nをいくつかの自然数の和に分ける方法の数p(n)に等しい。

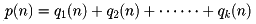
P(n)をnの分割数という。次に、n＝1, 2,……, 10の場合について、P(n)を示しておく。

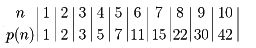
［古屋　茂］

カークマンの女生徒問題

15人の女生徒が毎日3人ずつ5組に分かれて散歩に出かける。1週間の間に15人のうちのどの2人も、ちょうど1回だけ同じ組になるようにするには、組分けをどのようにすればよいか。これがカークマンの女生徒問題である。カークマンは1847年にこの問題を提起しその解答を与えている。この問題の一つの解答をあげておく。15人の女生徒を1から15までの数で表す。

［古屋　茂］

マージャン総当りの問題

参加者が16人のマージャン会を開く。始めに4人ずつの組に分かれて4卓でゲームを行い、すべての卓で規定の勝負が終わったところで、組分けを別にして2回目の勝負に移る。これを続けて全体で5回の勝負を行うのであるが、16人のどの2人も5回のうちのちょうど1回だけ同じ卓でゲームをするようにしたい。どのような組合せをつくればよいかというのが問題である。

　次に一つの解答をあげる。16人を1から16までの数で表す。横に並んだ4人が同じ卓につくものとする。

［古屋　茂］

ラテン方格・オイラー方格

アルファベット（ラテン文字）を正方形の形に並べ、どの行どの列にも全部の文字がちょうど1個ずつあるように配列したもの（たとえば 次の図のように）をラテン方格またはラテン方陣という。

　　A B C D
　　B C D A
　　C D A B
　　D A B C
　フィッシャーは農事試験において実験を効果的に計画するためラテン方格の考えを利用した。ラテン方格において用いられている文字の個数をラテン方格の次数という。次数がnのラテン方格において、第1行および第1列が与えられた基準の順列であるものを標準形ラテン方格という。n次標準形ラテン方格がいくつあるか。その個数をL(n)で表すと

n次ラテン方格の総数はn!(n－1)!L(n)である。

　ラテン文字で書かれたラテン方格とギリシア文字で書かれたラテン方格とを重ねて、次図のように同一の対が現れないように配列したものをオイラー方格またはグレコ・ラテン方格という。

　　A_α B_β C_γ
　　B_γ C_α A_β
　　C_β A_γ B_α
　一般にn次ラテン方格を二つ重ねて正方形をなすn²個の欄にn²個の相異なる対が配置されているとき、それをn次オイラー方格という。nが奇数の場合とnが4の倍数の場合にオイラー方格をつくることは容易である。nが偶数で4の倍数でない場合にはオイラー方格は存在しないだろうとオイラーは予想した。二次オイラー方格が存在しないことは明らかである。六次オイラー方格が存在しないことはタリーG. Tarryが試行によって確かめた（1900）。1959年に至ってn≠2, n≠6のときn次オイラー方格がつくられることがボースRaj Chandra Boseや、パーカーErnest Tilden Parkerや、シュリクハンドShrikhandeによって証明された。

　カークマンの女生徒問題、マージャン総当りの問題、ラテン方格・オイラー方格はどれも、ある条件を満たすような配置を構成せよという問題である。このような型の問題に対しては有限体上の幾何学の考えが有効である。組合せ理論には多くの興味ある問題があるが、これらについては後記の文献をみられたい。

［古屋　茂］

『高橋磐郎著『組合せ理論とその応用』（1979・岩波全書）』▽『山本幸一著『数学入門シリーズ5　順列・組合せと確率』（1983・岩波書店）』▽『ホール著、岩堀信子訳『数学叢書15　組合せ理論』（1971・吉岡書店）』▽『C・ベルジュ著、野崎昭弘訳『組合せ論の基礎』（1973・サイエンス社）』

出典　小学館　日本大百科全書(ニッポニカ)

改訂新版　世界大百科事典

組合せ理論 (くみあわせりろん)
combinatorics

物の，組合せ的性質をもつ規則による選び方や，配列のしかたの数を考察する数学の一分野。組合せ数学とも呼ばれる。ある集合からいくつかのものを選び出す方法が何通りあるかを調べる順列・組合せの問題，多くの変数がいくつかの一次不等式を満たすという条件の下で，与えられた一次不等式を最大または最小にすることを考える線形計画法，一筆書きのようなグラフの組合せ的性質を調べること，オイラー方陣のような直交するラテン方陣の存在を考察するなど，これらは組合せ理論の例であり，数学のほとんど全分野に，その対象を見いだすことができる。分割数の問題（自然数nをいくつかの自然数の和で表す表し方は何通りあるのかという問題。例えばn＝5とすれば，5，4＋1，3＋2，3＋1＋1，2＋2＋1，2＋1＋1＋1，1＋1＋1＋1＋1の7通り）は，整数論と深く関わる。代数系の基本的対象である束や半群のおもな性質も組合せ的なものである。幾何学においても図形の組合せ的性質の研究は，主題の一つである。また，コンピューターのプログラムにおける組合せ的側面も重要な研究対象である。統計学においては，フィッシャーR.A.Fisherらによって始められた配置（デザイン）の理論を用いる実験計画法があげられる。とくにブロック配置block designは統計学にとどまらず，有限幾何学（有限集合からなるブロック配置で，例えば射影平面の公理のような幾何学の公理を満たすものの，組合せ的構造を研究する），ラテン方陣，分子構造などともつながりがある。さらに配置の自己同型群の研究から新しい有限単純群も発見された。このように組合せ理論は，組合せ的性質をもった配列の存在，配列の構成，配列のしかたの総数などの研究をできるだけ組織的に扱おうとするものであるが，上記のように雑多な内容を含んでいるため，組合せ理論としての統一性を求めることは困難である。
執筆者：西村 純一

出典　株式会社平凡社「改訂新版　世界大百科事典」