動的計画法（読み）ドウテキケイカクホウ（英語表記）dynamic programming

デジタル大辞泉

どうてき‐けいかくほう〔‐ケイクワクハフ〕【動的計画法】

予算、経営の長期計画の決定などに利用する数理計画法の一手法。組み合わせ爆発を起こすような、直接計算すると膨大な時間がかかってしまう問題に対し、途中までの計算を漸化式などで再帰的に用いることで計算効率を上げる。ダイナミックプログラミング。DP（dynamic programming）。

出典　小学館

精選版 日本国語大辞典

どうてき‐けいかくほう‥ケイクヮクハフ【動的計画法】

1. 〘 名詞 〙 ( [英語] dynamic programming の訳語 ) 時間の経過に伴う状況の変化を絶えず考慮し、各瞬間ごとに最適な政策を決定して最大の利益を得ようとする数理的計画法。投資計画、生産計画などに使われる。ＤＰ。

出典　精選版 日本国語大辞典

改訂新版　世界大百科事典

動的計画法 (どうてきけいかくほう)
dynamic programming

略称DP。ダイナミックプログラミングともいう。利得の最大や経費の最小のための条件を求める数理計画の方法は，問題の型によってさまざまであるが，動的計画法もその一つで，アメリカのベルマンRichard Bellmanが1950年ころから提唱し始めたものである。

　われわれの決定には1回だけで独立しているもののほかに，多段階的なものが多い。今期の決定が，次期における状況，可能な決定の範囲や効果等に影響を与えるというタイプのものである。今期の利得が大きくても，それが次期以降の利得を小さくする決定は必ずしも得策ではない。今期の決定は，次期以降の利得も計算に入れてはじめて最適なものになりうる。動的計画法は，このような多段決定過程の効果を数式によってモデル化し，その最適条件を求める方法を展開するものである。コンピューターによって数値解を直接求めるのに特に適しているので，オペレーションズリサーチ，自動制御，最適設計など多くの分野で活用されている。

　例をあげてみよう。図1のような道路網を考える。一方通行で北東あるいは南東だけに進める。土地に高低の差があり，交差点から次の交差点まで行くのに要する時間が場所によって異なるので，交差点Oから交差点Pへ最短時間で到達する経路を求めたい。

　交差点（i，y_i）と次の交差点（i＋1，y_i+1）に行くときに要する時間は図に書かれている通りであるが，これをg_i（y_i，y_i+1）と書けば（例，g₃（1，2）＝2），OからPに到る一つの経路y₀（＝0），y₁，y₂，……，y₈（＝0）に対する所要時間は

　g₀（y₀，y₁）＋g₁（y₁，y₂）＋……＋g₇（y₇，y₈）　……（1）　

と書ける。問題はこの式を最小にするy₁，y₂，……，y₇を求めることになる。もっとも，次にどの交差点に行けるのかは場所によって異なるので，交差点（i，y_i）の次に行ける交差点の集合をM_i（y_i）と書くことにすれば，y₁，y₂，……，y₇のおのおのはy_i+1∈M_i（y_i）をみたすものでなければならない（例，y₂＝0ならばM₂（0）＝｛1と－1｝，y₃は＋1または－1）。ところで，人が交差点にさしかかるたびに次に向かうべき交差点を選ぶものと考えれば，この問題は8段階（i＝0，1，……，7）にわたる多段決定過程と考えることができる。ここで，交差点の横座標iが決定の段階になるのは図からも明らかであろう。

　この考えを数学的に定式化するために，問題をちょっと一般化して，いま決定のi段目に交差点y_iにいるものとして，それ以後最終点Pに到るまでの経路を最適にする問題を考えて式の形にまとめれば，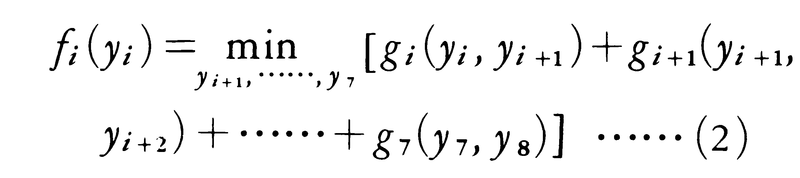

となる。ここで，右辺の［　］内はy_iからPに到る経路y_i，y_i+1，……，y₈の所要時間であるから，左辺の関数f_i（y_i）は交差点（i，y_i）からPまでに到る最短時間を示している。最終段階では，選択の余地がないから，

　f₇（y₇）＝g₇（y₇，y₈）＝g₇（y₇，0）（境界条件）　……（3）　

となる。またi＝0とすれば（2）式は交差点OからPへの最短経路を求めるもとの問題となる。

　（2）式について〈動的計画の漸化式〉とよばれる次の漸化式が成立する。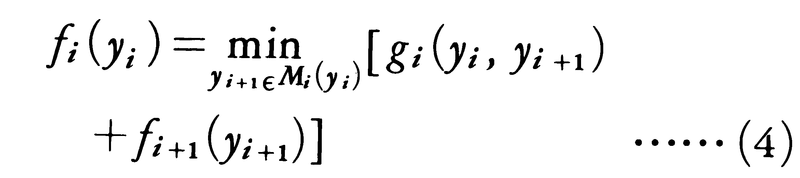

この式は次のように解釈できる。交差点y_iからPに到る最適経路は，次の交差点y_i+1からPに到る後半の部分も，y_i+1から始まってPに到る最適経路になっているはずである（ベルマンの最適性の原理）。そこで，y_iからy_i+1を通過し，y_i+1以降は最適な経路をたどるときの所要時間（（4）式の［　］内）が最小になるようなy_i+1を求めれば，これが次に通過すべき“最適な”交差点であり，その値こそはy_iからPに到る最小の所要時間f_i（y_i）である。

　（1）式のような最小（大）化問題を多段決定過程として，このような漸化式を導いて解を求めるのが動的計画法である。解を求めるには，普通，（3）式のような境界条件から始めて，漸化式を段階とは逆順に計算していく。上の例の場合には特に簡単で，図2，図3に示すように図上の一対比較で計算できるが，一般の場合でも，他によい方法がなければ，コンピューターによる総当り法も使える。得られた解はもとの問題の答を与えるばかりでなく，初期条件の変化の影響の見積り等にも役立つ。上の例でいえば，Oからの最適経路からはずれることがあっても，そのときの交差点からの最短経路が与えられている（図3）。このような感度分析が容易なのも動的計画法の特徴である。
執筆者：柳井 浩

図1～図3

出典　株式会社平凡社「改訂新版　世界大百科事典」

日本大百科全書(ニッポニカ)

動的計画法
どうてきけいかくほう

探索問題を解くための技法の一つ。探索空間中の異なる解が共通の部分問題をもつ場合に、その部分問題の解をメモリー上に蓄えることによって、同じ部分問題が繰り返し解かれないようにすることで効率をあげる。たとえば、東京から福岡までの最短経路を求める際、ある経路の探索の結果、大阪から福岡までの最短経路が得られたとする（部分問題の解）。この場合、別の経路の探索中に大阪に達したら、その後福岡までの最短経路はすでにわかっているので、あらためて計算する必要がない。これが動的計画法の基本的な考え方である。同じ部分問題が組合せ的に現れるために、単純な深さ優先探索や幅優先探索アルゴリズムでは指数関数的な計算時間がかかる場合でも、動的計画法によって多項式時間で計算できることがあり、その効果は絶大である。グラフの最短経路を求めるアルゴリズムとしてよく知られるダイクストラ法は、動的計画法のよい例である。

［丸山　宏　2019年4月16日］

[参照項目] | アルゴリズム

出典　小学館　日本大百科全書(ニッポニカ)

ブリタニカ国際大百科事典 小項目事典

動的計画法
どうてきけいかくほう
dynamic programming; DP

最適化の問題を多段階に分けて，逐次段階をふやしながら解いていく方法。各段階での最適化の構造は全体の構造より簡単であるため，1回で問題を解く代わりに比較的簡単な問題を多数回解くことによって計画全体を作成しようとするもの。通常は漸化関数方程式が導かれ，それを用いて問題が解かれている。 R.ベルマンが開発した数理計画法の一つであり，線形計画法 (リニア・プログラミング) と並んで重要な位置を占めている。最適経路問題や投資配分計画などがその主要な応用分野である。

出典　ブリタニカ国際大百科事典 小項目事典

百科事典マイペディア

動的計画法【どうてきけいかくほう】

ダイナミックプログラミングdynamic programmingとも。略称DP。最適性の原理を導入し，時間の流れとともに経過する現象の中で長期間を通じての最適決定を下す場合に適用される手法。たとえば企業の設備更新の時期を，長期間を通じての総利益が最大となるよう最適資源配分などを決定する場合などに適用。
→関連項目オペレーションズリサーチ

出典　株式会社平凡社

世界大百科事典（旧版）内の動的計画法の言及

【音声情報処理】より

…これは，両パターンが最もよく一致するように比較対象の一方の時間軸を非線形に伸縮しながら照合することによって解決できる。これは動的計画法dynamic programmingの技術を用いて実現でき，DPマッチングと呼ばれている。　もう一つの難しい点は，同じ単語でも話者によって発声されたスペクトルパターンが異なる点である。…

【最適化手法】より

…さらに制約条件が付加された場合には，線形計画法や非線形計画法が用いられる。また，多段階にわたる決定問題を対象とする最適化手法として動的計画法がある。　最適化手法は普通，現実問題の数学的模型に対して適用されるもので，現実問題それ自体を解いているのではない点に注意しなければならない。…

※「動的計画法」について言及している用語解説の一部を掲載しています。

出典｜株式会社平凡社「世界大百科事典（旧版）」