和田寧 (わだねい)
生没年:1787-1840(天明7-天保11)
幕末の数学者。円理表(定積分表)の完成者として著名。通称豊之進,初め香山直五郎政明という。字を子永,号は算学,または円象という。関流の日下誠の塾で数学を学ぶ。初め播州三日月藩士で,後に京都土御門家の算学棟梁,江戸芝の増上寺の寺侍となる。和田が創製した円理表は,ある関数をべき級数展開し,これを項別積分し,その値を求めた表である。その表には,例えば,
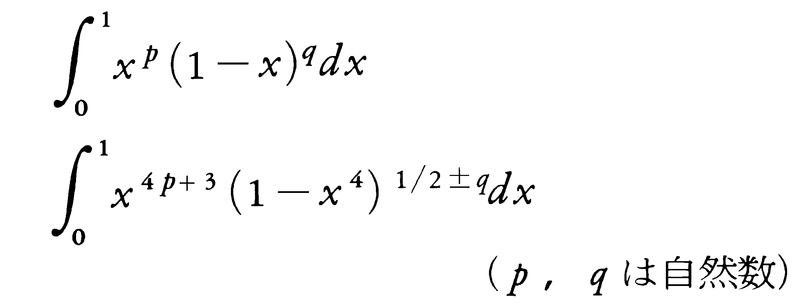
などが示されている。安島直円が創始した二重積分を一般の方法に拡張した。和田の円理表により,その当時流行した特殊な形の平面図形や立体図形の求積がたやすく求められるようになった。和田は微分に関しても,フェルマーの方法を発表している。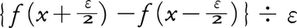 を計算し,ε=0と置いてf′(x)を求め,これを利用して極値を求めている。和田の塾には多くの著名な数学者が入門して円理表を教わっている。
を計算し,ε=0と置いてf′(x)を求め,これを利用して極値を求めている。和田の塾には多くの著名な数学者が入門して円理表を教わっている。
執筆者:下平 和夫
出典 株式会社平凡社「改訂新版 世界大百科事典」改訂新版 世界大百科事典について 情報
Sponserd by 
和田寧
わだやすし
[生]天明7(1787)
[没]天保11(1840)
文化文政期における和算の最盛期を開いた数学者。通称豊之進,字は子永,号は算学,円象,豁通など。日下誠の門下生となり,同門の内田五観とともに,関流宗統6伝についた。関孝和に次ぐ江戸時代の大数学者とされ,円理豁術 (かつじゅつ) の完成者である。和田は円理の基礎から論じて,安島直円による二重積分の方法の応用範囲を拡大し,円理に関する諸表をつくった。和算の円理はもっぱら級数を利用するため,無限級数を用いた円理綴術の展開に関する諸表が必要であった。整数術に関する著書も多いが,級数円理に関する著書および表には次のようなものがある。『六約算法』『だ表全書』『招差偏究算法』『円理諸表首巻』『順生率変歩表』『応率八態表』など。門下生は 170人を数えたという。
出典 ブリタニカ国際大百科事典 小項目事典ブリタニカ国際大百科事典 小項目事典について 情報
Sponserd by 
和田寧【わだねい】
江戸後期の和算家。名は〈やすし〉とも。通称豊之進。もと播磨(はりま)三日月藩士。江戸に出て日下誠に数学を学び,円理をいっそう発展させ,定積分表に相当するものを100以上作って計算を便利にした。曲線に関する研究もある。
→関連項目和算
出典 株式会社平凡社百科事典マイペディアについて 情報
Sponserd by 
和田寧 わだ-ねい
1787-1840 江戸時代後期の和算家。
天明7年生まれ。播磨(はりま)(兵庫県)三日月藩士。浪人となって江戸に出,日下誠(くさか-まこと)の門でまなぶ。のち芝増上寺の寺侍,京都土御門(つちみかど)家の算学棟梁(とうりょう)となった。円理表(定積分表)の完成者として知られ,関数の極値,異円なども研究。天保(てんぽう)11年9月18日死去。54歳。前名は香山政明。字(あざな)は子永。通称は直五郎,豊之進。号は算学,円象。
出典 講談社デジタル版 日本人名大辞典+Plusについて 情報 | 凡例
Sponserd by 
世界大百科事典(旧版)内の和田寧の言及
【円理】より
…このようなルーレットの問題や種々のサイクロイドの弧長やその曲線で囲まれた図形の面積の求積が盛んに研究され,これも円理と呼ばれた。また,これらの求長や求積の計算を簡便に行うために,多数の定積分表が和田寧により完成した。これらの積分表を円理豁術あるいは円理表という。…
【和算】より
…
[幕末の和算]
安島直円の弟子日下(くさか)誠(1764‐1839)は,多くの数学者を育てた。[和田寧](1787‐1840),[長谷川寛](1782‐1838),[内田五観](1805‐82)らである。和田は数多くの定積分表を作製し,それを弟子に与えた。…
※「和田寧」について言及している用語解説の一部を掲載しています。
出典|株式会社平凡社「世界大百科事典(旧版)」
Sponserd by 
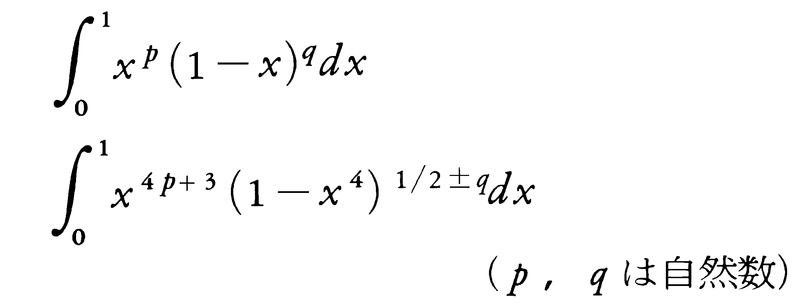
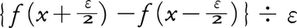 を計算し,ε=0と置いてf′(x)を求め,これを利用して極値を求めている。和田の塾には多くの著名な数学者が入門して円理表を教わっている。
を計算し,ε=0と置いてf′(x)を求め,これを利用して極値を求めている。和田の塾には多くの著名な数学者が入門して円理表を教わっている。
