最新 心理学事典 「意思決定」の解説
いしけってい
意思決定
decision making
【規範的意思決定理論normative decision theory】 規範的意思決定理論のモデル(以下,規範モデルと略記する)の代表的なものが,主観的期待効用モデルsubjective expected utility model(SEU)である。このモデルに従えば,個々の行動の望ましさは,その行動が引き起こす結果の効用によって測られる。ある行動が引き起こす結果が複数ある場合には,それぞれの結果の効用をその結果が生起する確率によって重み付けしたうえで平均を取った値がその行動の効用である。この行動の効用は,主観的確率分布による効用の期待値であり,主観的期待効用とよばれる。最適な行動とは,いくつかの選択肢の中でこの主観的期待効用が最も高いものである。規範モデルが,主観的期待効用モデル,あるいは期待効用最大化モデルmaximization of expected utility modelといわれることがあるのはこのためである。
主観確率も効用も主観的な評価値であるにもかかわらず,なぜこれが規範モデルといわれるのであろうか。その理由は,この主観的期待効用理論が少数の公理から導かれるからである。すなわち,物事の確からしさや望ましさの判断が推移律(たとえばa=bかつb=cならば,a=cであるという法則)を満たすなどの前提を認めるならば,主観確率も効用も数学的確率で定義することができる。
【記述的意思決定理論descriptive decision theory】 実際のわれわれの意思決定は,規範モデルが示唆するようになされているとは到底考えられない。まず,主観確率や効用を数値化して(すなわち,測定して),そのうえで期待値(重み付き平均)を計算していない。人間の意識的思考は言語によるところが大きい。数式も形式的には言語の一部であるが,通常のケースでは,数式的展開は利用可能ではないし,利用可能であるとしても当座には間に合わない。したがって,期待値を計算せず,最も高い期待値を示す選択肢(代替案)を選ぶという期待効用最大化も満たさない。このため心理学的研究においては,実際の意思決定行動の記述モデルとしての規範モデルに対する批判が数多くあり,また,心理学的プロセスや事実を記述するモデルも数多く提案されている。
サイモンSimon,H.A.が,人間が意思決定において必ずしも効用の最大化や決定の最適化をめざしていないことを指摘し,その代わりに,満足化satisfyingを提唱したことは有名である。これは限定合理性bounded rationalityとよばれる。規範モデルが想定しているのは,1回限りの決定において,選択肢の数と種類がすでに明示されており,それぞれの選択肢の後に起こる結果もわかっていて,数値的に評価できる状況であった。しかし,時間的に限られている実際の意思決定場面では,ベストを選ぶために多大な時間をかけるよりも,とりあえず,ベターを選ぶ決定をし,その決定が良い結果を生じなければその後の決定で修正すればよい。人間の実際の認知リソースを想定するときは,このような考え方が現実的である。
なお,限定合理性を制約条件下の最適化追求と解する立場もある。制約条件は種々考えられるが,一つの制約条件は,意思決定主体(人間や動物)のもつ認知能力の限界である。この場合は,サイモンのいう満足化原理と同じと考えてもいいであろう。別の制約として,利用可能なデータを考えることができる。全知全能ではない人間の場合,すべてを知って決定を行なうことができないので,決定のために使う情報が手元にあるデータからの情報に限られるという意味では現実的であるが,そのデータの情報の利用の仕方(たとえばベイズの定理を用いる)やどの程度どのようなデータを得るかという決定を含めると規範モデルのもつ現実性のなさと同じ問題を抱えている。
【主観確率や効用の不都合】 主観確率や効用は数学的な概念である(公理システムから導かれる効用は,本来確率である。ただし,通常は適当な線形変換をして,すなわち,尺度を変えて使われる)。したがって,これらは数学的概念として整合的でなければならないが,実際の日常的に行なわれる心理的確率や効用の評価は整合的であるとはいえない。また,客観的なデータが利用できるときにも,心理的確率評価値はこのデータからベイズの定理などによって数理的に導かれる予測値からずれることが多い。この点を早くから指摘しているのは,トベルスキーTversky,A.やカーネマンKarhneman,D.である。彼らの指摘のうちでも次の3点はとくによく知られている。
1.典型性representativeness 代表性ともいう。典型性によって評価する例として,いわゆるリンダ問題Linda problemを取り上げる。これは,リンダという人物の特徴(たとえば,率直で聡明,反核運動にも参加)などを知ったうえで,リンダが銀行の出納係であるか,出納係でありフェミニスト運動に参加しているかのどちらが可能性が高いかと問う場合,多数が,後者だと答える現象である。すなわち,それぞれのカテゴリーにリンダがどれほど近いか,典型的であるか,その程度によって可能性が評価されている。当然のことながら,後者は前者の下位集合であり,論理的に考えればつねに前者の可能性の方が高い。別の例としては,統計学の基本的な定理の一つであるところの大数の法則に対して,小数の法則law of small numbersとよばれる問題がある。たとえば,5回硬貨を投げたとする。二つの結果,A:表,表,表,表,表,B:表,裏,表,裏,裏のうち一つが得られたことがわかっている。いずれが事実であったか問われると通常はBと答える人が圧倒的に多い。しかし,もし,硬貨を投げた結果が互いに独立でかつその確率は変化しないとすると,この二つの結果が起こった可能性は等しい。特別なパターンをもっている事象と,適当に表と裏がばらついて分布するという事象とに分けた場合,適当にばらついているという事象の方が数も多く典型的である。そのため,事象の確率がその概念の典型性の程度によって影響されたと考えられる。小数の法則というのは,大数であれば,表の確率は0.5に近づくが小数ではその限りではないということからくるらしいが,本質的にはこの間違いは大数の法則には関係がない。
2.利用可能性availability この性質を説明するための有名な設問は次のとおりである。「英単語において,最初にrが来る単語と3番目にrがある単語ではどちらが多いか?」。通常の答えは,最初にrが来る単語が多いというものであろう。しかし,実際に辞書で調べてみると3番目にrが来る単語の方が多い。事象の確率を問う場合,想起できるケースをカウントする方略を取ると,想起できるケース,すなわち,確率評価者に利用可能なケースの数は前者が多いことが理由である。
3.調整と係留adjustment and anchoring 確率評価(割合の評価を含む)の際に,判断のよりどころとなる数値が事前に与えられるとき,その値に影響されることをいう。規範モデルが,経済学で応用されるとき,当然のことながら,金額は額面そのものの価値と同じではないことは認識されている。金額の効用は効用関数で評価されるべきであり,これは線形ではなく,一般に非線形である。ただし,経済学の応用の多くの場合,効用関数は状況によって変わらないとされる。しかし,実際場面での効用の評価は状況によって左右される。同じ金額でもそれが損失とみなされる場合,利益だとみなされる場合,あまり労力をかけることなく手に入れた場合,本来の目的と異なる支出の場合等々で容易に異なる効用値を取る。これを根拠とし,規範モデルに対する批判の理由とされることがある。
【プロスペクト理論prospect theory】 トベルスキーやカーネマンは,規範モデルが適切ではないとし,それに従わない事象を統一的に説明しようとして,プロスペクト理論を提唱した。たとえば,意思決定者にとって,状況によって効用が変化することを考慮して,効用の代わりに,価値関数value functionという用語を用いる。また,主観確率も意思決定状況によって決定に及ぼす影響が異なるため,さらに確率を修正する加重関数を導入する。たとえば,金額の価値関数は,損失分岐点を参照点として,損失は凹の関数であり,利益は凸の関数であるとされる。加重関数は,確実なものに規範モデルが予測する以上の価値を見いだすことの説明(確実性効果)などのために用いられる。
繰り返しになるが,主観確率は数学的確率であり,互いに背反な事象において,どちらかが起こる確率はそれぞれの確率の和である。これは当然のように見えるが,実際の確率評価においてこの法則をあらゆる組み合わせにおいて成立させるのは難しい。ファジィ測度(ショケ積分。すなわちファジィ積分の一手法)を利用して,この加法性を緩め,より一般的に人間の意思決定を叙述するための理論が累積プロスペクト理論cumulative prospect theoryである。
【ヒューリスティックスheuristics】 規範モデルが指示する決定の方略自体は,必ずしも日常的な決定を描写しているわけではない。また,規範モデルを合理的なものとして受け入れるとしても,行動の選択には,それが引き起こす結果をリストアップし,それぞれの結果の効用を評価する必要がある。それぞれの結果は数多くの属性をもっており,それらの属性をここに評価し,それらの相互作用を加味しつつ総合して結果の効用を評価するのは不可能に近い。規範モデルを実践的なモデルとして使うためには,なんらかの簡便化が必要である。完璧ではないが,ある程度正しい答を得ることのできる実践的な方法をヒューリスティックスとよぶ。たとえば,それぞれの効用の重み付き加算点を考えることは,最も単純な総合方式である。しかし,属性の効用はもともと加算的ではなく,総合された加算点が真の効用と一致しないことも多い。属性の効用が線形的に表現されることを(属性の)効用独立というが,効用独立が成立する条件は現実的ではないことが多い。因子分析などを利用して,属性の直交化を行なった後に加算するなどの工夫が必要であろう。効用の評価と選択確率を結びつけるモデルとしては,以下のようなものがある。
1.BTLモデルBradley-Terry-Luce model BTLモデルは,個々の選択肢の効用の評価から選択確率を導く有名なモデルである。このモデルは,選択される確率がそれぞれの効用に比例するという単純なモデルであるが,元々は実際の意思決定のモデルとして提案された記述モデルである。
2.属性消去モデル(EBAモデルelimination by aspects model) 現実の意思決定はある瞬間に起こるものではなく,ある程度の時間の枠内で時系列的に行なわれる。EBAモデルは時系列的なモデルである。たとえば,複数の商品から一つ選ぶとする。まず考えつくある商品の属性(たとえば金額)を選び,その属性において望ましい商品のみを残す。EBAモデルでは,重要な属性として思いつく確率が,それぞれの効用に比例するとされる。それでもまだ複数の選択肢が残っているならば,別の属性を選ぶ。たとえば,その商品の色について,望ましいもののみ残す。このようなプロセスを繰り返し,一つに絞られたときに決定が終わる。
3.後悔の理論 人間の意思決定が,意思決定時の効用評価によるのではなく,将来のある時点を想定し,その場での後悔を評価し,その後悔を最も小さくするような決定の仕方をする。効用の直接的評価値そのものではなく,将来の時点から見て後悔するであろうというふうに複雑に変形された形で決定に影響する。
4.高速・倹約ヒューリスティックスfast and furgal heuristics ギゲレンツァGigerenzer,G.らのグループが提唱する単純なルールの集まりである。人間が現実に行なっていることは,進化的な裏づけをもち,現実への適応のため瞬時に決定するために有効なものであるとされる。
【ベイズ的モデルの復興】 ここまでの記述においては,規範モデルが実際の意思決定行動の記述モデルとして役に立たないという主張を紹介した。しかし,この主張に対する批判もある。この批判の正当性を吟味するためには,規範モデルのベイズ的アプローチの原点に戻る必要がある。ベイズ統計学の創始者たち,たとえばド・フィネッティde Finetti,B.,ジェフリーズJeffreys,H.,ド・グルートde Groot,M.H.などがまとめたベイズ的体系においては,理性的な人間ならば当然遵守すべきいくつかの公理を掲げ,そこから数学的確率と効用を導出している。さらに,期待効用を最大化する選択肢を選ぶことが良い決定であることも,公理論的に導いている。
本項の記述では,合理性ということばを意思決定の目的を遂げるために有効であるという意味で用いているが,「ある系において,前提を認める限り,整合性(首尾一貫性)がある」という意味で用いることもある。整合性をもつという意味ではベイズ統計学は合理的である。整合的である限り,主観確率も効用も意思決定者が自由に値を定めてよい。主観確率や効用が,状況によって数値や順序が変化することは合理的体系としてのベイズ的アプローチを批判したことにならないのである。実際,自由に確率や効用の値を定められるならば,ベイズ的アプローチは規範にはなりえないという意見すら存在している。
心理学的研究においてもベイズ的アプローチの心理学的意味を再吟味し,その意味を深く探ろうとする動きが,オークスフォードOaksford,M.やチェイターChater,N.などの議論から出されている。規範モデルであれ,記述モデルであれ,モデルと現実のデータの間に乖離があるのは避けがたいことであり,その乖離の心理学的意味を問うことが意思決定において大事である。この規範モデルと現実データとの乖離は,主観確率と効用の分離,確率の加法性などの数学的要請,数値的な最適化などが人間の思考のプロセスと合致しないことが本質であり,この違いが人間の意思決定のプロセスの特徴を明らかにしている。さらに,ベイズ統計学では,データによる学習はベイズの定理によってなされるが,ベイズの定理の前提は,種々のデータのそれぞれが得られる確率,すなわちデータ発生モデルがあらかじめ与えられており,データによる学習による確率の変化はこの発生モデルから得られたデータからのみに依存するとされる。この点も実際の人間の学習と大きく異なる点である。いずれにしろ,規範モデルと記述モデルの関係は二者択一的な単純な問題ではなく,議論すべきことが多い。
【処方モデルprescriptive model】 規範モデルか記述モデルかという議論ではなく,心理学的応用の場面で意思決定のモデルが役に立つことが重要であると考える立場もある。応用のために用いられる意思決定のモデルを処方モデルという。記述モデルといえども,モデルである以上,現実と完全に一致することはありえない。また規範モデルといえども,現実から遊離したモデルであれば,実質科学では受け入れられない。
そのような中で最初から役に立つことを目的とする実践的数理モデルも存在する。多属性効用モデルmulti-attribute utility modelは,効用を評価したい結果が複数の属性(多属性)をもつとき,それらを総合するためのモデルである。
線形的な効用の評価としては,階層構造を用いて属性の重要度とそれぞれの属性における各選択肢(代替案)の望ましさを総合する巧みな方法があり,階層分析法analytic hierarchy process(AHP)とよばれる。また,マーケティング分野でも消費者の意思決定プロセスの描写に関心があり,その代表的なモデルとして多項ロジットモデルmultiple logit modelがある。
【数理モデルとしての展開】 心理測定法やマーケティングでは,モデルを数理的に扱う習慣がある。意思決定に関するここまでの説明を数理的に整理する。
選択肢(代替案)がm個あるとする。これらはどれか一つを選べばそのほかの代替案を取る可能性は消えるというふうに整理されている。これらを,a1,a2,…,amとする。代替案jの効用は,その代替案を立てた場合に生起するnj個の結果cj1,cj2,…,cjnの効用u(cj1),u(cj2),…,u(cjn)とそれぞれの結果が起こると予想する主観確率P(cj1),P(cj2),…,P(cjn)によって次のように期待効用として表現される。
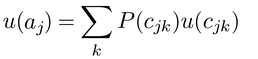
規範的意思決定理論によれば,意思決定とはこの期待効用を最も大きくする代替案を選択することである。しかし,現実の意思決定行動は規範モデルが指し示すようにならないことは明らかである。効用や主観確率が一意的に定められることはありえないし,われわれの決定は状況によって容易に変わる。結果がほぼ完璧に予想され,代替案が一つの結果のみに対応するとき,たとえば商品の選択のような場合には商品を選ぶことが,すなわちその商品が得られるという結果につながるが,このような簡単な場合でも,その選択は一意ではなく,確率概念を用いてこのばらつきを表現する。今n個の結果(たとえば商品)C={c1,c2,…,cn}のうち,cjを選ぶ確率は,サーストンThurstone,L.L.の一対比較の法則law of paired comparisonが有名であるが,これもそれぞれの結果の効用が正規分布に従って分布するというモデルであるとみなされる。心理学の選択モデルとして有名な別の例は,前述のBTLモデルである。C={c1,c2,…,cn}からcjを選ぶ確率は,
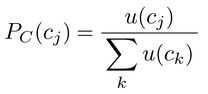
となる。今,結果cjがp個の属性sj1,sj2,…,sjpによって成り立っているとする。それぞれの属性の値の効用が測定可能だとする。結果cjの効用をこれらの属性によって表現するとき最も簡単なのは線形結合である。すなわち,
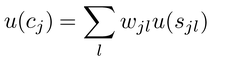
となる。この重みを計算する方法の一つが階層分析法である。マーケティングにおける消費者行動のモデルは実用的な観点から見てもある程度複雑になっている。たとえば,商品の集合C={c1,c2,…,cn} のうち,cjを選ぶ確率は
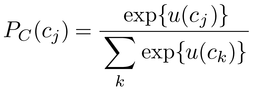
となる。もし,各商品の効用が属性の効用の線形和である場合には,
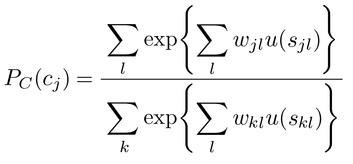
となる。 →思考
〔繁桝 算男〕
出典 最新 心理学事典最新 心理学事典について 情報

