移動平均法 (いどうへいきんほう)
moving average method
時系列,あるいは定常過程の表現法の一つであって未来を予測するのに用いられる。時間の経過により新しいデータが得られると,以前の一定期間のデータと併せて逐次それらの代表値を更新していく平均方法である。もっとも簡単なのは同じウェイトで一定期間の相加平均をとる方法で単純移動平均法という。例えば6,7,8月と3ヵ月間の生産実績から9月の生産高を予測するのに,既知の3ヵ月間のデータの算術平均を用いる。そして9月の実績が知られたら,6月は捨てて7,8,9月のデータから10月を予測する。このほか,すぐ前の月は重視しそれ以前はウェイトを減らしていく方法があり,加重移動平均法と呼ばれる。上の例で,6,7,8月の量をそれぞれA1,A2,A3とするとき,例えば(3A3+2A2+A1)/6で9月を予測する。9月の実績が知られたら7,8,9月の量をそれぞれA1,A2,A3とすればよい。一般により多くの過去にさかのぼれば,また適切なウェイトをとれば,ゆらぎが平滑化され,よい予測が得られる。そこでのウェイトは時系列の構造によって決まる。これらの理論的根拠は時系列の移動平均表現にある。長期傾向や季節変動などを除いた平均値0の時系列{Xn;-∞<n<∞}があり,分散は有限だとする。もしそれが-∞の過去に初期情報のない純非決定的な時系列であれば,無相関な時系列{Yn;-∞<n<∞}(Ynの平均値は0,分散は1)と係数{an}があり,各Xnは,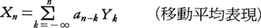 と表され,しかも各nについて{Xk;k≦n}の張る空間と{Yk;k≦n}の張る空間とが等しい。とくにガウス過程のときは両者の情報は一致する。そして{Xn}について時刻mまでの量{Xk;k≦m}が観測されたときXn(n>m)の最良な(線形)予測値は
と表され,しかも各nについて{Xk;k≦n}の張る空間と{Yk;k≦n}の張る空間とが等しい。とくにガウス過程のときは両者の情報は一致する。そして{Xn}について時刻mまでの量{Xk;k≦m}が観測されたときXn(n>m)の最良な(線形)予測値は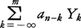 で与えられるが,それはまた上記の関係からXk(k≦m)の加重平均になるのである。ここで用いられる係数anは{Xn}の共分散関数から求められる。時間を連続にした定常過程の場合にも同様な理論がある。
で与えられるが,それはまた上記の関係からXk(k≦m)の加重平均になるのである。ここで用いられる係数anは{Xn}の共分散関数から求められる。時間を連続にした定常過程の場合にも同様な理論がある。
執筆者:飛田 武幸
出典 株式会社平凡社「改訂新版 世界大百科事典」改訂新版 世界大百科事典について 情報
Sponserd by 
移動平均法
いどうへいきんほう
method of moving average
(1) 経済統計の時系列から傾向変動を見出すための方法の一つ。経済時系列を解析する際に顕著な周期性をもつ波の影響を除去するためにしばしば用いられている。時系列の各時点 t の値 xt を中心にして一定区間の平均値を求め,同一時系列の全期間について,平均する区間を順次移動させながら平均値を求めて,この平均値の系列 yt をもとの時系列の傾向変動とみなすのである。 yt はまた時系列になる。多くは平均する数値の項数は奇数個となるが,偶数個の場合には,一種の加重移動平均を行う。たとえば,12ヵ月移動平均の場合には,最初と最後の項に 1/2 のウエイトをつけて 1/24 とし,他の項は 1/12 として平均を計算すれば,12ヵ月で繰返される波はすべて除去されることになる。また時系列の解析においては,yt が先に与えられているときに xt として各時点ごとに無相関な時系列を考え,これの移動平均により yt を表わす移動平均過程というモデルがよく用いられる。 (2) 受入時点により単価の異なる材料や商品の払出価額および期末棚卸価額を算出する方法の一つ。材料ないし商品を新たに受入れるたびに,受入金額をその時点の残高金額に加えた合計額を,受入数量と残高数量の合計で割って加重平均単価を決定し,それを以後の払出単価にする方法である。受入れのたびに単価を改訂するので,継続的記録が要求される。払出時にいつでも払出単価が明確にできる長所があるが,受入回数が多いと計算がめんどうであるうえ,単価に端数の出る場合が多いという欠点もある。
出典 ブリタニカ国際大百科事典 小項目事典ブリタニカ国際大百科事典 小項目事典について 情報
Sponserd by 
移動平均法【いどうへいきんほう】
時系列に並ぶデータがあるときに,1項ずつ項をずらしながら平均を求める方法。たとえば4項移動平均とは,原データの第1項から第4項までの平均,第2項から第5項までの平均,第3項から第6項までの平均といったように求められる。将来予測に用いられ,時間経過による新データを得ると,以前のデータとあわせてそれらの代表値を更新するもの。マクロ経済統計などで,季節的要因による経済変動や不規則変動を取り除く目的で12ヵ月移動平均が求められる。また株式相場では,各銘柄に対して6日移動平均や25日移動平均などを用いて,株価予測の一助とする。
出典 株式会社平凡社百科事典マイペディアについて 情報
Sponserd by 
移動平均法
販売用語として、2つの用法がある。販売高が、一時的な要因によって異常に上下していることがある場合、このような要因を排除し、傾向的変動を把握する方法。短期間の平均をとり、つぎに一期ずらして平均値をとり、何年間かの平均値をみる。移動平均値を決めることによって、販売の傾向的な動向を分析することができる。棚卸資産の払出原価計算法のひとつ。新しく品物を仕入れたら、そのつど前の在庫を加えて平均したものを原価とし、その平均原価を払出原価とする。
出典 (株)ジェリコ・コンサルティング流通用語辞典について 情報
Sponserd by 
移動平均法
そのつどの残高と受入高の平均により払い出し単価を計算する方法を移動平均法といいます。
出典 (株)シクミカ:運営「会計用語キーワード辞典」会計用語キーワード辞典について 情報
Sponserd by 
世界大百科事典(旧版)内の移動平均法の言及
【時系列分析】より
…ここで,mtはなめらかな動きの成分,ytはその動きからのずれを表す。mtを抽出するにはフリーハンドで曲線を引くのも一つの手であるが,前後を含めた3個のデータの平均,すなわち 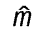 t=(xt-1+xt+xt+1)/3で推定する3点移動平均法をはじめ,多点の重み付き平均をとる一般的な移動平均法が古くから考察され使用されている。移動平均法の一つの欠点は全体的な傾向から一つだけ著しくはずれた値があるとき,その影響が強く残存することで,そのような危険をさけるため移動中央値法(前後3点や5点の中央値をmtと推定する方法)を組み合わせて利用する方法も工夫されている。…
t=(xt-1+xt+xt+1)/3で推定する3点移動平均法をはじめ,多点の重み付き平均をとる一般的な移動平均法が古くから考察され使用されている。移動平均法の一つの欠点は全体的な傾向から一つだけ著しくはずれた値があるとき,その影響が強く残存することで,そのような危険をさけるため移動中央値法(前後3点や5点の中央値をmtと推定する方法)を組み合わせて利用する方法も工夫されている。…
※「移動平均法」について言及している用語解説の一部を掲載しています。
出典|株式会社平凡社「世界大百科事典(旧版)」
Sponserd by 
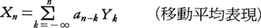 と表され,しかも各nについて{Xk;k≦n}の張る空間と{Yk;k≦n}の張る空間とが等しい。とくにガウス過程のときは両者の情報は一致する。そして{Xn}について時刻mまでの量{Xk;k≦m}が観測されたときXn(n>m)の最良な(線形)予測値は
と表され,しかも各nについて{Xk;k≦n}の張る空間と{Yk;k≦n}の張る空間とが等しい。とくにガウス過程のときは両者の情報は一致する。そして{Xn}について時刻mまでの量{Xk;k≦m}が観測されたときXn(n>m)の最良な(線形)予測値は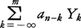 で与えられるが,それはまた上記の関係からXk(k≦m)の加重平均になるのである。ここで用いられる係数anは{Xn}の共分散関数から求められる。時間を連続にした定常過程の場合にも同様な理論がある。
で与えられるが,それはまた上記の関係からXk(k≦m)の加重平均になるのである。ここで用いられる係数anは{Xn}の共分散関数から求められる。時間を連続にした定常過程の場合にも同様な理論がある。
