単振動（読み）タンシンドウ（その他表記）simple harmonic oscillation

デジタル大辞泉

たん‐しんどう【単振動】

最も基本的な振動で、等速円運動をその円の直径上に投影したのと同じように動く、物体の往復運動。往復に要する時間を周期、半径を振幅という。単調和振動。調和振動。

出典　小学館

精選版 日本国語大辞典

たん‐しんどう【単振動】

1. 〘 名詞 〙
2. ① 振り子の行なう鉛直面内の往復運動のように、運動体がいつもある定点からの距離に比例する力をうけて引き戻されるように動く振動。振れの最大値を振幅、一往復に要する時間を周期という。振動のうち最も単純で基本的なもので、複雑な振動はいくつかの単振動に分解することができる。
3. ② 等速円運動をしている点を直径に正射影した点の往復運動。点の座標をｘ、時間をｔとすれば、x=Asin(wt+a)という形の関係がある（Ａ、ｗ、ａは定数）。

出典　精選版 日本国語大辞典

ブリタニカ国際大百科事典 小項目事典

単振動
たんしんどう
simple harmonic oscillation

調和振動または単調和振動ともいう。時間の正弦関数または余弦関数で表わされる周期運動。ゴム紐やつる巻きばねにつるされた物体は単振動をする。一般に1つの定点からの距離に比例して常にこの点に向う力を受けて直線運動する質点は定点を中心として単振動し，質点の定点からの変位 x は時間 t の関数として x＝A sin (ωt＋δ) で表わされる。 A を振幅，ωt＋δ を位相，δ を位相定数，ω を角振動数という。質点が1秒間に振動する回数を振動数といい，ν＝ω/2π である。したがって，1回振動するのに要する時間，すなわち周期 T は T＝1/ν＝2π/ω となる。周期 T は振幅 A の大小に関係せず，これを単振動の等時性という。安定な平衡点にある質点を少しずらして離すと，質点は平衡点を中心として近似的に単振動する。単振り子が小さい振幅では単振動し，等時性をもつのはこの例である。単振動は最も簡単な振動であるだけでなく，どんな複雑な周期振動もいくつかの単振動の和で表わすことができ (これを調和解析という) ，この意味でも単振動は最も基本的な振動である。単振動をする質点を調和振動子という。等速円運動する質点を1つの直径上に正射影した影点の運動は単振動である。また，ねじられた物体が角変位に比例する復元的なトルク (力のモーメント) を受けるときには，回転的な単振動をする。ねじり振り子はその一例である。

出典　ブリタニカ国際大百科事典 小項目事典

日本大百科全書(ニッポニカ)

単振動
たんしんどう

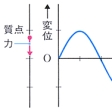
一直線上を運動する質点に、その直線上の原点からの変位に比例する復元力が働く場合には、質点の変位は時間の経過とともに正弦関数的な変化をして振動する。この振動を単振動とよぶ。単振動をする質点が、ある運動状態（ある変位とある速度をもつ状態）になってから、ふたたび同じ運動状態になるまでの時間を振動の周期という。周期の逆数を振動数（または周波数）とよび、振動数に2πラジアン（360度）を掛けた積を角振動数（または角周波数）とよぶ。質点の変位の最大値を振幅という。変位は、振幅に位相とよばれる量の正弦関数を掛けた積に等しい。位相は、その時刻ゼロにおける値（初位相）に角振動数と時刻との積を加えた和に等しい。

　単振動をする質点の力学的エネルギーは、その運動エネルギー（質点の質量と速度の二乗との積の半分）と位置のエネルギー（復元力の変位に対する比例定数と変位の二乗との積の半分）との和に等しい。

　単振動をする質点の力学的エネルギーの値は、力学的エネルギーの保存則に従い、一定に保たれる。

　ばねで吊(つ)るしたおもりが真空中で上下振動するとき、このおもりの重心は単振動をする。単振り子の振幅が小さいとき、単振り子のおもりの重心の振動は単振動に近い。

［飼沼芳郎］

[参照項目] | 振動

単振動（周期と振幅）

出典　小学館　日本大百科全書(ニッポニカ)

百科事典マイペディア

単振動【たんしんどう】

振動の中心からの距離xが，時間tの正弦関数または余弦関数，つまりx＝A sin（ωt＋ε）の形で表される振動。ここでAは振幅，２π/ωが周期，ω/2πが振動数，ωt＋εは振動の位相である。一般の振動は振動数の異なるいくつかの単振動に分解されるが，そのうち振動数が最も小さいものを基本振動という。
→関連項目位相（物理）｜振動｜振動数｜振幅｜単振子

出典　株式会社平凡社

世界大百科事典（旧版）内の単振動の言及

【運動】より

…簡単な直線運動の例としてa(t)＝a₀の等加速度運動を考えると，t＝0での位置座標x₀，速度v₀とすると，x(t)＝x₀＋v₀t＋1/2(a₀t²)，v(t)＝v₀＋a₀tとなる。また，振幅A，角振動数ωの単振動では，x(t)＝Acosωt,v(t)＝－Aωsinωt,a(t)＝－Aω²cosωt＝－ω²x(t)である。(2)平面や空間内での曲線運動　一般の運動のときにはある定まった点(原点O)から物体の位置Pに向けて引いた矢印，すなわち位置ベクトルr＝の動きが時間tの関数として知れれば運動がわかったといえる。…

【三角関数】より

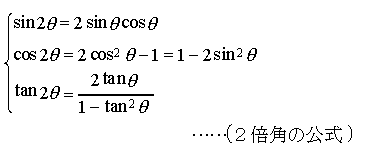
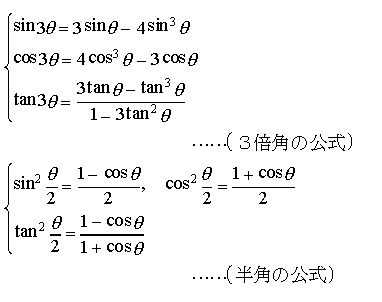
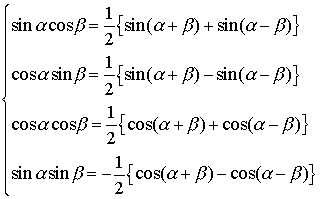
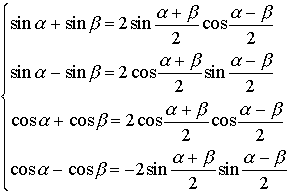…次の公式はド･モアブルの定理と呼ばれ，複素数の累乗，累乗根などの計算に使われる。nを正の整数，iを虚数単位とすると，　(cosθ＋isinθ)ⁿ＝cosnθ＋isinnθ
［単振動］
　図3において，OPが一定の角速度ωで回転しているとし，時間t＝0のときθ＝αであったとする。Pからx軸，y軸に垂線PQ,PRをおろすと，点Q,Rはそれぞれx軸，y軸上で時間tの関数として，　x＝rcos(ωt＋α)，y＝rsin(ωt＋α)で表される運動をする。…

【振動】より

…振動は自然の中でしばしば見られる基本的な現象の型であり，その理論は種々の現象を理論的に解明する一つの重要な手法ともなっている。波動
［単振動］
　さまざまな振動の中でもっとも単純でしかも基本的なものが単振動である。具体的な例として，つる巻きばねでつるしたおもりの上下の振動を考えよう。…

※「単振動」について言及している用語解説の一部を掲載しています。

出典｜株式会社平凡社「世界大百科事典（旧版）」