計算図表（読み）ケイサンズヒョウ

デジタル大辞泉

けいさん‐ずひょう〔‐ヅヘウ〕【計算図表】

いくつかの変数の間に関数関係があるとき、それを図表に示し、既知の変数の値に対して未知の変数の値を求められるようにしたもの。ノモグラフ。

出典　小学館

精選版 日本国語大辞典

けいさん‐ずひょう‥ヅヘウ【計算図表】

1. 〘 名詞 〙 計算を簡便に行なうために用いる図表。二つ以上の変数について成り立つ関係式を図示し、変数間の対応する具体的な数値を読みとれるようにしたもの。ノモグラフ。

出典　精選版 日本国語大辞典

日本大百科全書(ニッポニカ)

計算図表
けいさんずひょう

普通、三つ以上の変数の間に成り立つ関係式を図表で表し、簡単に関係が読み取れるようにしたもので、共点図表と共線図表がある。

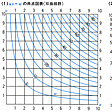
　共点図表は、変数の関係を満たす値の組が線の交点として求められるようにしたもので、たとえばuv＝wの場合、wに特定の数値を与えれば、uとvの関係は双曲線になるので、uv＝wの共点図表は図A(1)のような双曲線群になる。もしuv＝wの両辺の対数をとればlogu＋logv＝logwとなるので、対数方眼紙を利用すれば、uv＝wの共点図表は図A(2)のような直線群に変換できる。一般に共点図表は作成に手間がかかり、使用する場合も目分量による補間がむずかしく、次に述べる共線図表に比べると劣る。

　共線図表は、変数の値の関係を1本の直線で読み取れるようにしたもので、次にいくつかの基本型を例として解説してみよう。

基本型〔1〕　f₁(u)＋f₂(v)＝f₃(w)　加法の共線図表で、三平行線型図表といわれる。図B(1)のようにm : nの間隔に平行に引かれた3本の直線上に
　　x＝mf₁(u), y＝nf₂(v),
　　z＝｛mn/(m＋n)｝f₃(w)
の関数目盛りを目盛ると、目盛りu、v、wの間にf₁(u)＋f₂(v)＝f₃(w)の関係式が成り立つ。x＝mf(u)の関数目盛りまたは関数尺というのは、uの値u₁、u₂、……に応じて原点からx₁＝f(u₁), x₂＝f(u₂),……の距離に相当する点にu₁、u₂、……と記入してつくられたものである。ピタゴラスの定理によって、直角三角形の辺の長さを求める図表をつくるには、a²＋b²＝c²からm＝n＝1とすればx＝a², y＝b², z＝(1/2)c²の関数目盛りを目盛ればよい（図B(2)）。

基本型〔2〕　f₁(u)・f₂(v)＝f₃(w)　乗法の共線図表で、Z字型図表といわれる。図C(1)のように線分AB＝kの両端を通って平行線を引きZ字型の図形をつくり
　　x＝mk/｛m＋nf₁(u)｝,
　　y＝mf₂(v), z＝nf₃(w)
の関数目盛りを目盛れば、u、v、wの間にf₁(u)・f₂(v)＝f₃(w)の関係式が成り立つ。図C(2)はuv＝wの共線図表である。基本型〔2〕は、両辺の対数をとればlogf₁(u)＋logf₂(v)＝logf₃(w)となるから、対数尺を利用することによって基本型〔1〕の共線図表にすることもできる。

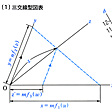
基本型〔3〕　1/｛f₁(u)｝＋1/｛f₂(v)｝＋1/｛f₃(w)｝　三交線型図表といわれる。図D(1)のように、1点Oから出る3本の直線を引き、Ox上にはx＝mf₁(u)、Oy上にはy＝nf₂(v)を目盛る。次にOx上にz′＝mf₃(w)を目盛ってから、その目盛りをOyに平行な直線によってOz上に射影してOz上に目盛る。するとu、v、wの間に基本型〔3〕の関係式が成り立つ。ここでm＝nと置けば、OzはOxとOyのつくる角の二等分線となる。レンズの公式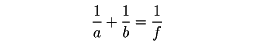

の共線図表は、∠xOy＝120゜Ozをその二等分線とすれば、すべての軸の目盛りは同じになり、図D(2)のようになる。

［片野善一郎］

計算図表の歴史

共線図表は、1884年、フランスのエコール・ポリテクニクの教授で工学者・数学者であったモーリス・ドカーニュMaurice d'Ocagne（1862―1938）によって創案されたもので、彼はこのような図表をノモグラムnomogram、それを対象とする学問をノモグラフィnomographyとよんだ。計算図表学は公式の図示法を研究する応用数学の一分科として始められたものであるが、一度つくっておけば永久的に反復使用できる便利さがあるので、微積分の計算や定型の代数方程式、微分方程式の解の算出などにも利用され、理工学はもちろん、医学や経済学など広範囲の分野で活用されるようになった。

［片野善一郎］

『小倉金之助著『計算図表』（1940・岩波全書）』

共点図表〔図A〕

共線図表の基本型〔1〕〔図B〕

共線図表の基本型〔2〕〔図C〕

共線図表の基本型〔3〕〔図D〕

出典　小学館　日本大百科全書(ニッポニカ)

改訂新版　世界大百科事典

計算図表 (けいさんずひょう)
nomography

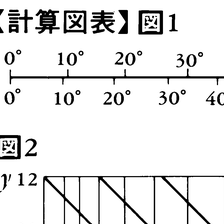
計算を迅速かつ簡単に行う手段として用いられる図表。この図表を使った計算を図式計算法という。計算図表の原型はかなり古くから見いだされるが，学問としての体系化は19世紀後半に主としてフランスの学者たちによって行われ，なかでもドカーニュMaurice d'Ocagne（1862-1938）は共線図表の創案によって，計算図表学第一の功労者とされている。もっとも簡単なのは1変数の関数f（x）を表示する場合で，1直線上の基準点からf（x）の長さのところにxという目盛を印した関数尺がある。f（x）＝log xのときは対数尺と呼ばれ計算尺に用いられる。同じく1直線を使ったもので，2変数の間の関数関係F（x，y）＝0を表す背合せ尺がある。例えばsin x＝tan yを表すのに図1のように直線の上側は左からtanyの長さのところにyと目盛り，下側はsinxのところにxと目盛る。これによってx＝30°のときsin 30°（＝1/2）＝tan yとなるyはほぼ26.5°であることがすぐにわかる。3変数の関数関係F（x，y，z）＝0を表すのには，平面上にいくつかの直線，または曲線の群を描いた計算図表が用いられる。実用上便利なのにマッソーJunius Massauによって開発された共点図表があり（1884），とくに3直線群からなる場合が重要である。そうなるための条件は与えられた関数関係が1変数関数f₁，f₂，f₃，g₁，g₂，g₃，h₁，h₂，h₃を用いて，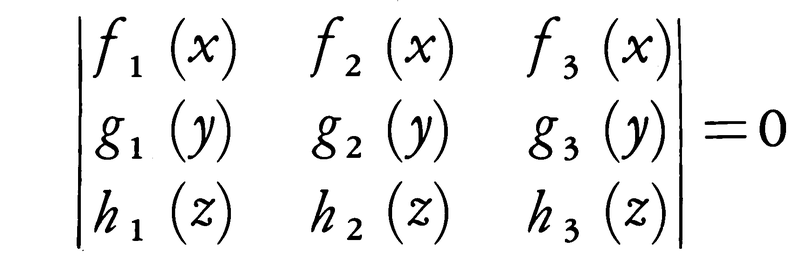

と表されることである。例えば直角三角形の3辺の関係x²＋y²＝z²は，

であり3直線群，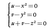

からなる共点図表を描くことができる。u＝x²は一群の縦線であり，v＝y²は横線，u＋v＝z²は斜線であって，図2からx，y，zの関係（近似値）が読みとれる。3変数の場合，もう一種類の重要な例は共線図表である。例えばz＝x・yに対する共線図表は，log z＝log x＋log yであることを用いて図3のように3本の対数尺を用いる。中央の線には両側のものの2乗の目盛が刻まれているので，x，yの点を結ぶ線が通る点zは1/2（log x＋log y）＝1/2log xyの高さを表すが，2乗の目盛がしてあるので，z＝x・yを読みとることができる。共線図表でほかによく知られた例としては，年利率r，期間n年で元金1に対する元利合計A＝（1＋r）ⁿを計算する図表（図4）がよく知られている。多変数の関数関係を表示する計算図表も種々くふうされているが複雑すぎる感がある。計算尺と同様，近年急速に普及した小型コンピューターの影響で計算図表の利用は激減したが，計算が視覚に訴えて理解されること，近似値が瞬時に求まる点などの利点がありいくらかは利用されている。
執筆者：飛田 武幸

図1～図4

出典　株式会社平凡社「改訂新版　世界大百科事典」

百科事典マイペディア

計算図表【けいさんずひょう】

数値計算を簡便に行うための図表。２個以上の変数の間に成り立つ関係を図示して，その間の数値の関係を簡単に読みとれるようにしたもの。与えられた関係を満足する変数値の組が曲線群（または直線群）の交点により表されるものを共点図表，与えられた関係を満足する変数値を表す点の組が同じ直線上にのるように作ったものを共線図表（ノモグラム）という。→計算尺
→関連項目図式計算法

出典　株式会社平凡社

ブリタニカ国際大百科事典 小項目事典

計算図表
けいさんずひょう

「ノモグラフ」のページをご覧ください。

出典　ブリタニカ国際大百科事典 小項目事典