計算尺（読み）ケイサンジャク

デジタル大辞泉

けいさん‐じゃく【計算尺】

乗法・除法・開平・開立などの計算を簡単に行うことができる、物差し形の計算器具。固定された二つの台尺、その間を移動する滑尺、目盛りを合わせて値を求めるカーソルからなる。

出典　小学館

精選版 日本国語大辞典

けいさん‐じゃく【計算尺】

1. 〘 名詞 〙 計算器具の一つ。固定した二つの目盛り尺（台尺）と、その間を滑り動く一つの目盛り尺（滑り尺）とからなり、カーソルを移動して目盛りを合わせ、値を求める。乗法、除法、開平、開立などの計算結果の近似値を簡単に求めることができる。スライドルール。〔物理学術語和英仏独対訳字書（1888）〕

出典　精選版 日本国語大辞典

日本大百科全書(ニッポニカ)

計算尺
けいさんじゃく

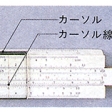
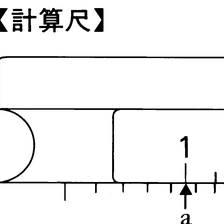
二つ以上の対数尺を相互に移動させて、乗除計算をはじめとして、比例、平方、立方、三角関数、対数その他の近似計算が簡単にできるようにくふうされた計算器具。直線型と丸型の2種類があるが、一般には直線型が使われる。また、用途によって、一般事務用、一般技術用、特殊用途用などのものがつくられている。計算尺は、固定された尺（台尺または外尺という）、移動する尺（滑尺または内尺あるいは中尺という）、各尺の目盛りをあわせるために表面を移動するカーソルの三つからできている（図A）。

［片野善一郎］

計算尺の目盛り

計算尺にはいろいろな目盛りがあるが、基準になるのはC尺とD尺である。これは
　　log1＝0, log2＝0.301, log3＝0.477,……
であるから、左端の目盛りを1とし、もし目盛りの全長がlの計算尺ならば0.301lのところに2、0.477lのところに3を目盛るというようにつくられたものである。CI尺、DI尺は逆C尺、逆D尺といわれるもので、C尺、D尺の目盛りを右から左へ目盛ったものである。また、CF尺、DF尺はずらし尺といわれるもので、C尺、D尺の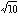のところで切断して左右に移動させたものである。C尺の1にCF尺の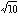が対応し、CF尺の中央の目盛りが1になるようにつくられているもので、C尺、D尺の計算で目はずれになるときに使われるものである。A尺、B尺は2単位尺で、D尺を半分に縮めて同じ尺を2本継いだものである。

　　loga＝(1/2)loga²
であるから、D尺のaにはA尺のa²が対応する。A尺、B尺は平方、平方根の計算に使う。同様にK尺は3単位尺で、立方、立方根の計算に使う。そのほか内尺の裏にはS尺（logsinaの目盛り）、T尺（logtanaの目盛り）、SI尺、TI尺、L尺（等間隔の目盛りで常用対数を求めるときに使う）など、用途によりいろいろな目盛りがくふうされている。

［片野善一郎］

計算尺による計算法

計算の原理は対数の性質
　　log_ab＝log_a＋log_b,
　　log_(a/b)＝log_a－log_b
などを利用したもので、乗除計算の基本は図Bのとおりである。計算尺を使うときは、位取り、小数点の位置は概算で求めなければならない。19.8×4.2, 1.98×0.42はともに1.98×4.2＝8.32を求め、概算で20×4＝80, 2×0.4＝0.8のように位を定めて、答え83.2,0.832を出す。

［片野善一郎］

計算尺の歴史

イギリスの天文学者エドマンド・ガンターEdmund Gunter（1581―1626）は1620年にガンター尺とよばれる対数尺を考案し、コンパスを使って航海上の問題を解く計算に利用した。このガンター尺を2本相互に移動させることによって、コンパスを使わずに計算できるようにしたのはイギリスのウィリアム・オートレッドである。オートレッドは、円板の周上に目盛りを施した丸型計算尺を最初に発明した人でもある。計算尺はイギリスでしだいに改良されていくが、とくにジョン・ロバートソンJohn Robertson（1712―1776）は真鍮(しんちゅう)製の薄片でカーソルをつくり実用価値を高めたという。現在の計算尺に近いものは1850年ころ、フランスの砲兵将校アメデー・マネームAmédée Mannheim（1831―1906）によって発明された。彼の計算尺はフランスの全砲兵部隊に採用されてから、マンハイム型という名称でよばれるほど普及したという。

　日本へ計算尺が渡来したのは、1894年（明治27）に工学博士広田理太郎(りたろう)と当時の内務省土木課長近藤虎五郎(とらごろう)の2人が欧米視察の土産(みやげ)の一部として持ち帰ったマンハイム計算尺が最初であるという。その後、当時度器の目盛り工だった逸見治郎(へんみじろう)（1878―1953）が日本特有の竹製計算尺を発明し普及させた。

［片野善一郎］

『宮崎治助著『計算尺発達史』（1956・オーム社）』

計算尺の各部名称〔図A〕

計算尺による計算法（乗除計算の基本）〔…

出典　小学館　日本大百科全書(ニッポニカ)

改訂新版　世界大百科事典

計算尺 (けいさんじゃく)
slide rule

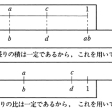
乗除算をはじめとし，平方，立方，三角関数などの計算を簡便にできるようにくふうされた器具。1620年，イギリスのガンターEdmund Gunter（1581-1626）の考案した対数目盛を応用したものが計算尺の原型で，その後オートレッドWilliam Oughtred（1574-1660）らによって改良が加えられ，カーソルがついた現在の形の計算尺は，1850年ころフランスのマネームAmédée Mannheim（1831-1906）のものが最初である。固定された台尺とこれに平行に動かせる滑尺と呼ばれる2種類のものさしからなり，どちらにも同じ尺度の目盛が刻まれていて，一方を滑らせ目盛を合わせることにより，対数の値の加減を求めて2数の積と商を計算することができる。すなわち，2正数a，bの積の対数はそれぞれの対数の和になっていること，log ab＝log a＋log bを利用する。図のように二つのものさしを向かい合わせ，両者とも1と記した起点からlog xの長さのところにxという目盛が記されている。aの印のところに他方のものさしの1を合わせbの目盛の下を見れば，起点からlog a＋log bだけ離れたところであり，目盛から答えabが読みとれる。割算はこれを逆に行えばよい。19世紀に入って今日のような形式のlog－logの目盛をもった計算尺と呼ばれるものが考案され，平方や開平などの計算にも利用され広く普及した。しかし近年は携帯用の電卓にその役割を譲ってしまった。
執筆者：飛田 武幸

図－計算尺

出典　株式会社平凡社「改訂新版　世界大百科事典」

ブリタニカ国際大百科事典 小項目事典

計算尺
けいさんじゃく
slide rule

簡便な携帯用アナログ計算器。対数目盛りをもつ固定尺と滑尺があり，滑尺を滑らせて計算操作を行う。原理は，対数により乗除算を加減算に変換できることを利用したもので，目盛りを正しく読むためのカーソル (滑子) がついている。乗除，開平，開立，べき，三角関数などの計算ができ，また特に各工業分野の特殊計算に便利なようにつくった電気用，機械用，土木測量用その他の特殊計算尺がある。温度や外力に対し寸法変化の少い材料でつくる必要があるが，日本では幸いに廉価でこの条件に適する竹があるので，竹にセルロイドを張った製品が多く，優秀である。外国では以前はセルロイド製や紙製が多く狂いやすかったが，その後プラスチックを使ったよいものができている。形式は直線目盛りのものさし型が最も多いが，2枚以上の目盛りつき円盤を同心的に重ね，回転して計算する薄型のものもある。近年は電子式卓上計算器，コンピュータの普及により，一般にはあまり使用されなくなった。

出典　ブリタニカ国際大百科事典 小項目事典

百科事典マイペディア

計算尺【けいさんじゃく】

対数の性質を利用して乗・除・開平・三角関数・対数等の計算を近似的に簡便に行う器具。ふつう対数目盛を刻んだ固定尺とその間をすべる滑尺があり，固定尺にまたがって動くカーソルの線を目盛に合わせて計算する。しかし近年は携帯用の電卓にその役割を譲ってしまった。→計算図表
→関連項目アナログ計算機｜対数目盛

出典　株式会社平凡社

世界大百科事典（旧版）内の計算尺の言及

【アナログコンピューター】より

…アナログコンピューターは，現在広く利用されているディジタル技術を核としたディジタルコンピューターの普及に先だって，シミュレーターや科学技術計算に広く活用されたアナログ技術を核とした計算機である。　数値や変数を長さ，電圧，回転角などのように連続的は物理量に置き換えて，物理現象の数学的関係を用いて相似的に計算する計算機で，もっとも手近な例として計算尺がある。もっとも広く用いられたアナログコンピューターは数値を電圧などの電気量に置き換えて計算し，解は電気量と時間の関係で示される。…

※「計算尺」について言及している用語解説の一部を掲載しています。

出典｜株式会社平凡社「世界大百科事典（旧版）」