信頼性（読み）しんらいせい（英語表記）reliability

最新 心理学事典

しんらいせい
信頼性
reliability

テスト理論における信頼性とは，テスト得点を真の得点と誤差に分けたとき，テスト得点のばらつきのうち，真の得点のばらつきが占める割合のことである。この定義により，信頼性が高ければ高いほどテストの質は高いことがわかる。真の得点true scoreとは，同じテストを何度も（理論的には無限回）繰り返し実施して得られたテスト得点の平均である。同じテストとは，測定の目的とする性質（構成概念）が共通であり，かつ真の得点が同じであるテストを指す。同じテストの繰り返しのそれぞれにおいて得られるテスト得点は，真の得点が同じでも，誤差の部分が変動するため，異なる値を取る。

【信頼性の推定】　信頼性の推定のために，真の得点が同じで誤差の部分は真の得点と独立であり，その分散の大きさは被験者を通して等しい二つのテストの相関係数が信頼性係数に等しいという事実を利用する。真の得点が同じで，誤差の分散が等しいような二つのテストを平行テストparallel testという。信頼性係数を推定する方法の基本は，二つの平行テストの間の相関係数を得る方法であるといってもよいが，そのための具体的方法にはいくつかの種類がある。すなわち，

⑴平行テスト法parallel test estimation method　二つのテストを平行テストになるように開発し，適切なサンプルに実施して相関係数を得る。この方法は，テストを作るための労力が大きく，しばしば実現が困難である。以下の方法は，平行テストを二つ作る方法より簡便である。

⑵再テスト法test-retest estimation method　同じテストを2回実施して，その二つの結果の相関係数を得る。これは，わかりやすい方法であるが，1回目のテストの結果が2回目のテストに影響を与えないことが前提である。たとえば，1回目のテストの答えを記憶していることが有利な影響を与える場合や，1回目の受験によって，テスト内容に関して学習できる場合には，この2回のテストは平行テストであるとはいえない。このような欠点はあるが，再テスト法は，テスト得点が時間の経過によってどの程度の変動を生じるか，すなわち時間的安定性を評価できる利点がある。

⑶折半法split-half estimation method　テストを構成する項目を二つの平行テストになるように，二つの等質な群に分け，その間の相関係数を計算する。ただし，この相関係数は，二つに分けられたテストの信頼係数であり，もともとのテストの信頼性係数は，スピアマン-ブラウンの公式によって復元される必要がある。すなわち折半されたテスト間の相関係数をｒ^hとするとき，信頼性係数ｒは，

　ｒ＝

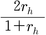
となる。とくに，項目の並び方に特段の規則性がない場合に，奇数番目の項目と偶数番目の項目それぞれの合計を別の二つのテストとみなすことがある。折半法は二つの平行テストに分けたが，三つや四つ，あるいはそれ以上の平行テストに分けることも可能である。ｎ個の部分テストに分けた場合に，もともとのテストの信頼性係数は，それぞれの部分テスト間の相関が同じであるとき（ｒ^pとおく），

　ｒ＝

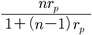
によって得られる。この方法は，先に説明した方法の一般化であり，スピアマン-ブラウン21の方法Spearman-Brown formula 21とよばれる。

　テストをいくつかの平行テストに分けることは可能であるが，可能ではあっても現実には難しい。平行テストではなくても，いくつかの条件を満たせば信頼性係数の推定を行なうことができる。平行テストの厳密性を一般化した仮定の代表的なものは，タウ線形とよばれる仮定と，本質的タウ線形と呼ばれる仮定である。タウ線形の仮定は，部分テストｊの真の得点（τ^j）とテストｋの真の得点（τ^k）の間に，

　

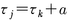
という関係がある場合をいう。

　本質的タウ線形の仮定は二つのテストの間の関係をさらに拡張し，

　

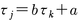
というように，二つの真の得点間に線形関係が成立する場合を指す。部分テストが，本質的タウの仮定を満たす場合に，信頼性係数の推定値を与えるのが，クロンバックのα係数Cronbach's α coefficientである。この係数は，本質的タウの仮定を満たさないときには，信頼性の推定値としては低めの値を与えることが多い。その意味では，クロンバックのα係数は，信頼性係数の評価として保守的で慎重な推定値であるといえる。

　本質的タウの仮定よりも平行性の要件をさらに緩め，二つのテストが共通の因子によって説明されるという仮定をおくことがある。これは因子分析モデルにほかならない。この定義に従ってどの程度の信頼性をテストがもつかについては，因子分析の共通性の推定値が指標になる。すなわち共通性が大きいほど，信頼性が高いということになる。α係数も因子分析における共通性も，時間的に安定しているかどうかの意味での信頼性の評価値にはなりえず，テストの等質性の指標である。

【測定の標準誤差standard error for measurement】　テストの信頼性を示す指標として，信頼性係数を中心として説明してきたが，信頼性を示すために，誤差の標準偏差を用いることがある。これを測定の標準誤差という。標準誤差は，推定値や予測値などの統計量の標準偏差を示す用語でもあるので，差異化するためにとくに「測定の標準誤差」という。ただし，単に標準誤差とよばれることもある。測定の標準誤差は，各被験者に対して一定であることを仮定している。言い換えれば，どのような真の値に対応する測定の標準誤差も同じであることを仮定している。

　一方，古典的テスト理論に対して，現代的テスト理論とも称される項目反応理論を利用すれば，さまざまな真の得点のそれぞれを所与として測定の標準誤差を推定することができる。

【一般化可能性generalizability】　一般化可能性とは，どの程度の範囲内で安全性を保つかを示す概念である。統計学的には，真の得点のモデルと分散分析モデルは類似したモデルである。すなわち真の得点のモデルは，分散分析の一元配置モデルと同じであり，意味のあるパラメータは，各個人ごとの真の得点である。分散分析モデルの文脈においては，信頼性係数の推定の問題は，単純な測定モデル（一元配置的）の分散の推定の問題である。個人ｉに対するｋ回目の繰り返しにおける測定値ｘは真の得点τと誤差εに分け，次のように書くことができる。

　

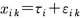
上の式のモデルにおいて，τⁱとε^ikの分散を推定してσ^2x＝σ^2τ＋σ^2εという関係を利用して，ｒ＝σ^2τ／σ^2xを計算する。ところで，分散分析が用いられる実験計画法において，複数の要因が関与する場合があるように，テスト得点のばらつきに影響する要因が個人の真の得点だけではなく，ほかにも複数の要因があるときがある。たとえば，論述試験に対して，複数の評定者がおり，それぞれの評定者によって評価が違うとすると，被験者ｉを評定者ｊが採点したｋ番目の結果ｘ^ijkは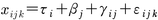，となる（ここで，β^jは評定者の効果。γ^ijは，個人と評定者との交互作用を示す）。信頼性は，評定者の偏りを残差とみなすならば，二元配置分散分析によって，分散成分を推定し，ｘの分散のうち，τの分散とｘの分散の比を取って，信頼性係数の推定値とする。真の得点を期待値として定義したが，この期待値は，同じ被験者に対して同じ条件における繰り返しにおける平均である。しかし，条件が異なると期待値も異なる。先述の例では，被験者の真の得点以外に安定して得られる意味のあるパラメータとして評定者を想定したが，そのほかの要因も想定できる。適切な分散分析モデルを仮定し，想定したパラメータのうち，真の得点とみなすべきパラメータの和の分散が，テスト得点の分散のうちどの程度を説明するかを問う手法を一般化可能性の理論とよぶ。単純な信頼性係数の推定の場合よりも，テスト得点がどのような状況で使われるのかに対応して実際的なテスト作製のために有用な情報となる。　→項目反応理論　→古典的テスト理論　→妥当性
〔繁桝 算男〕

出典　最新 心理学事典

改訂新版　世界大百科事典

信頼性 (しんらいせい)
reliability

工学分野でいう信頼性とは，JISによれば〈対象が与えられた条件で，規定の期間中，要求された機能を果たすことが出来る性質〉と定義されている（JIS Z 8115）。ここでいう対象とは必ずしも物ばかりでなく，コンピュータープログラムのようなソフトウェアや人間行動を含む概念である。また，信頼度も英語ではreliabilityであるが，信頼度とは，上述の性質のかわりに確率で信頼性を表現したものである。たとえば，宇宙船の信頼度90%とは，打ち上げた10台の宇宙船のうち1台が故障（機能喪失）するということを意味している。類似の概念に安全性がある。信頼性は機能に重点が置かれ，安全性は人命，財産の確保に重点が置かれているが，工学的方法や管理は共通性が高い。

　信頼性の対象となるものは，それが故障することにより，社会的に，また企業や個人にとって，安全性を含めて経済的損失をまねく恐れのあるもので，たとえば原子力プラント，工場設備，ロボット，コンピューター，車両，航空機，家庭用製品など多岐にわたり，その規模も大きなシステムから部品・材料のような小さなものまでを含むことになる。システムが複雑になると，たった一つの部品の故障や人間の誤りが全システムの故障につながりかねないため，大きなシステムの信頼性の確保には，それを構成する部品・材料，ソフトウェア（コンピュータープログラムや文書），人間の高信頼性が要求される。かつてアポロ宇宙船の部品信頼度は0.999999を必要とするといわれた理由はここにあり，この技術を信頼性工学reliability engineeringと呼んでいる。また，技術のみならず総合管理の仕事が重要であり，これを信頼性管理と呼んでいる。信頼性工学は，第2次大戦を契機として発展し，1950年代にその基礎が固まり，世界的に拡大した。特に近年，品質管理の分野において，いわゆる〈品質保証〉に不可欠な工学として，信頼性の手法が取り入れられるようになった。

　製品の信頼性保証は，その対象の企画，設計，製造，試験・検査，使用，保全から廃却までの一生（ライフサイクル）が関係してくる。特に，製造に先だつ設計段階において，考えられる故障原因をいかに取り除いておくかという点が重要であり，このような技術を信頼性設計reliability designと呼んでいる。信頼性設計においては，過去の失敗事例，成功事例を十分に研究解析して，新設計に織り込む必要がある。このため各種の技術データ（故障データを含む）を集約し，技術計算，技術試験を行い，実使用時にどれくらいの信頼度を実現しうるかの予測，すなわち信頼度の予測を行う。この一方法として，故障モード影響解析や故障の木解析などの手法が使われている。特に高い信頼度が要求される部分には，ちょうどスペアタイヤと同じように，そこに故障が発生しても，もう一つあるいはそれ以上の余分な手段を用意しておき，機能が果たせるような工夫がほどこされる。これを冗長設計と呼んでいる。高信頼化のためには，故障しにくい部品材料を選ぶとか，試作品や製品を実働条件と同じような環境で試験する環境試験や耐久試験も重要な手法であり，実使用前に問題点を摘出して改善することができる。また，設計のいくつかの段階で経験豊富な技術者や管理者が専門的立場から設計の可否を評価する設計審査design reviewの仕事も重要である。信頼性設計では，単に故障しないことを保証するだけでは不十分で，故障や異常をいち早く検出・診断して修復する能力が重視される。この能力を保全性maintainabilityと呼び，そのような設計を特に保全性設計と呼んでいる。製品は故障しない信頼性と修復容易な保全性とを同時に備えてはじめてバランスのとれた設計となり，この二つが満足されると，高い可動率（アベイラビリティ）availabilityを示すことになる。
→安全性　→故障
執筆者：塩見 弘

出典　株式会社平凡社「改訂新版　世界大百科事典」

ブリタニカ国際大百科事典 小項目事典

信頼性
しんらいせい
reliability

機械や電子部品などが，どの程度故障しないで，所定の機能を果すかという程度を表わす用語。故障要因について物理的原因にさかのぼって，確率論，推理統計学を利用し，また品質管理の面から解明し，総合したデータの判定結果から信頼性を決めることができる。そのときの判定結果を信頼度という。より正確な信頼度を得るためには，できるだけ多くの実験を繰返さなければならない。最重要ではあるが，最も困難なことは，故障要因の加速を行うことである。このようにして加速係数を定めることができれば，きわめて短時間に多くの実験を繰返して信頼度を高めることが可能となる。加速を行わせるために最も一般的なものは温度である。

出典　ブリタニカ国際大百科事典 小項目事典

栄養・生化学辞典

信頼性

　→再現性

出典　朝倉書店

世界大百科事典（旧版）内の信頼性の言及

【故障】より

…信頼性工学においては，信頼性や保全性に関する数量的尺度を信頼性特性値と呼んでいる。このなかには，信頼度reliability(信頼性)のほか，保全性に対する保全度maintainabilityがある。これは，対象に故障が発生したとき，ある規定の期間内(たとえば1時間以内)に修復を完了する確率である。…

【安全性】より

…JIS（ジス）では，安全性を〈人間の死傷又は資材に損失若しくは損傷を与えるような状態のないこと〉と定義している(JIS Z 8115(1981))。一般にシステムあるいは製品を新しく開発するに当たっては，所要の性能を確保し，所定の寿命の間は，その使命の達成を阻害する機能上の故障を起こさず(信頼性)，使用者あるいは一般大衆の生命，財産に危険を与えないこと(安全性)が要求される。信頼性では使命達成を妨げる故障を主対象とするのに対し，安全性では不可抗力の天災，あるいは人間が予期しない事象または不注意によって起きる危険な状態(ハザードhazard)を対象とし，このような状態になったとき，人命あるいは資材の損失または損傷を伴う事故の発生を防止するか，万一事故が発生したときは，それによる被害を最小にするための事後処理を含め，使用者および一般大衆の生命と財産を守ることを目的とする。…

※「信頼性」について言及している用語解説の一部を掲載しています。

出典｜株式会社平凡社「世界大百科事典（旧版）」