最新 心理学事典 「古典的テスト理論」の解説
こてんてきテストりろん
古典的テスト理論
classical test theory
【真の得点true score】 テスト得点のうち,誤差を除いた系統的な部分を真の得点とよぶ。ただし,これを真の得点とよぶのは,誤解を招く可能性がある。テストによって得ようとする情報そのものとは,同じではないからである。ここで,測定の対象者,すなわち被験者をiとし,テストの得点をxiとする。また,このテストが測定しようとしている潜在的な特性をθiとする。このθiは直接観測されず,操作的にも定義できない。これに対して操作可能な概念が,「真の得点τi」である。真の得点とは,同じ条件で,同じ被験者に対し繰り返しテストを実施した得点の平均である。ただし,この平均は観測値の平均ではなく,無限回の繰り返しをした場合に想定される平均として定義される。すなわち,真の得点は繰り返しのモデルとする理論分布の期待値である。以上のことを数式で示すと,被験者iに対するk回目の繰り返しにおけるテスト得点xikは,真の得点τiと誤差の部分εikに分けられる。真の得点は,
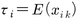
として定義される。ここで,Eは期待値(理論上の平均値)を意味し,結局,
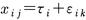
となる。
【信頼性reliability】 被験者iが固定されているとき,τiは定数であるが,誤差は定まらず分散をもつ。繰り返しkが固定されていないことを,*で表わすとき,
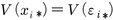
である。ここでVは分散を意味する。また,被験者の母集団からどのiがサンプルされるかによるばらつきの分散をσ2τとする。さらに分散V(εi*)が被験者iによらず一定であるとし,V(εi*)=σ2εとおく。このとき,真の得点と誤差とはなんら関連がなく,確率的に独立であるという仮定を追加すると,母集団から任意の被験者が選ばれ,テストを受ける場合の得点のばらつきは次のように分解される。
σ2x=σ2τ+σ2ε
テストの信頼性とは,テスト得点xのばらつきのうち,真の得点τのばらつきが占める割合である。もちろん,この割合は高ければ高い方がよい。信頼性係数は,テストを2回実施した場合の相関係数,同じ真の得点をもつ二つのテスト間の相関係数,折半したテスト間の相関係数の関数,分散分析による分散の比の推定などによって推定される。
【妥当性validity】 妥当性の定義は時代とともに大きく変わっている。ケリーKelley,T.L.(1927)は,妥当性を「テストが測定しようとするものを実際に測っている程度」としている。これは今でもよく見られる定義であり,わかりやすいが,十分に明確ではなく,具体的ではない。ギルフォードGuilford,J.P.(1946)は,「テストはそれが相関するものはなんであれ,それに対して妥当である」とした。これは思い切った具体的な定義であり,一般的でわかりやすい。反面,一般的過ぎて,妥当性の概念を散漫にしている。信頼性が,テスト得点と真の得点間の関係を論じているのに対し,妥当性は,テスト得点とそもそもの測定の目標との間の関係を推論しているといえる。それだけに,妥当性の検証は信頼性以上に難しく,またその推論の背景も多様である。妥当性については,新しい分類の仕方も提案されている。
【標準化standardization】 古典的テスト理論の重要な概念として,信頼性と妥当性のほかに標準化が挙げられる。標準化とは,テスト得点が基準集団に対して意味をもつ場合である。たとえば,中学生の学力試験を開発しようとする場合,全国の中学生が基準集団である。標準化のためには,この基準集団から標本を抽出し,データを得て,テスト得点の相対的位置を標準化された得点とする。単純に平均と標準偏差をそろえる場合や,正規分布に合わせた得点(正規化されたパーセンタイル得点)の場合などがある。できるだけ基準集団を代表するような標本を選ぶ問題は,標本抽出理論による。また,標本によって得られるデータの分布(ヒストグラム)を理論的に基準集団の真の分布に近づけるために,分布の凸凹を滑らかにする統計的操作,すなわちスムージングを適用する場合もある。 →項目反応理論 →信頼性 →妥当性 →テスト →標準化
〔繁桝 算男〕
出典 最新 心理学事典最新 心理学事典について 情報

