パウリの原理（読み）パウリノゲンリ（英語表記）Pauli's principle

デジタル大辞泉

パウリ‐の‐げんり【パウリの原理】

一つの原子内では、2個以上の電子が同時にエネルギー・スピンなどの同じ状態をとることはないという原理。パウリが発見。禁制原理。排他原理。排他律。→構成原理1

出典　小学館

精選版 日本国語大辞典

パウリ の 原理(げんり)

1. 一九二五年物理学者パウリによって発見、確立されたもので、多量の電子を含む系で、二個以上の電子が等しい量子状態をとることはあり得ないという法則。

出典　精選版 日本国語大辞典

日本大百科全書(ニッポニカ)

パウリの原理
ぱうりのげんり
Pauli's principle

2個以上の電子や陽子は同じ状態を同時にとることができないとする原理で、禁制原理、排他原理または排他律ともいう。ここでいう状態とは、原子、分子、原子核やこれらを構成する粒子のとる量子的状態のことである。量子的状態を表すには、一組みの整数あるいは半整数（整数プラス1/2）を用いることが多い。パウリは1924年この原理を発見し、指定したn,h,j,mの値をもつ電子は原子内に1個より多く存在することができないことを提唱した。パウリの原理においては、電子のほか、フェルミ粒子すなわち陽子やμ(ミュー)中間子などのスピンが、半整数の粒子に対しても成り立つことが、相対性理論とエネルギー最低値存在の仮定のもとに示されている。

　2個のフェルミ粒子の量子的状態を状態関数(x₁,x₂)とする。ここでx₁、x₂はそれぞれの粒子の座標とする。x₁とx₂とが等しいときにも状態関数がゼロでないとすれば、2粒子は同じ量子的状態をとっていることとなって、パウリの原理に反する。いいかえれば、を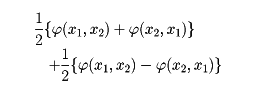

の二つの項に分けたとき前の項がゼロとなる。したがって状態関数は座標の交換に対して符号を変える、すなわち反対称でなければならない。一般にフェルミ粒子の系の状態関数は、任意の二組みの粒子のスピンや座標などの力学変数の交換に対して反対称になっている。この条件はフェルミ粒子の系の状態に強い制限を課す結果となる。

［田中　一］

[参照項目] | パウリ

出典　小学館　日本大百科全書(ニッポニカ)

改訂新版　世界大百科事典

パウリの原理 (パウリのげんり)
Pauli's principle

原子の状態は，その原子に固有な各電子軌道に何個の電子が入っているかによって規定されるが，同一の軌道には反対向きのスピンをもつ電子が各1個ずつ，すなわち，合計2個までしか入れないという量子力学の原理をパウリの原理という。スピンまで指定すると，一つの電子状態にすでに電子が1個入っていれば，第2の電子はその状態に入れないことになるので，排他律exclusion principle，禁制原理ともいう。原子スペクトルの異常ゼーマン効果と原子構造を説明するために，1924年，W.パウリが仮説として導入した。当初は原子内の電子の量子数として，今日の主量子数，方位量子数，磁気量子数に対応する3個のほかに第4の量子数があると仮定されたが，すぐ後にG.E.ウーレンベックとS.A.ハウトスミットによってそれがスピンであることが示された。

　パウリの原理は同種粒子を2個以上含む量子力学系の対称性に関するより一般的な原理から導かれる。すなわち，このような系の波動関数は同種粒子を互いに入れかえたとき，まったく変わらないか（対称），符号だけが変わるか（反対称）のいずれかだけが可能であり，スピンが整数の粒子（ボース粒子）では前者，半整数の粒子（フェルミ粒子）では後者が成り立つ。後者の場合，粒子がほぼ独立に軌道運動していればパウリの原理が成立する。スピン1/2の電子，中性子，陽子や半整数スピンの原子核はパウリの原理に従うが，スピン1の光子やスピン0の中間子，整数スピンの原子核は従わない。パウリの原理を統計集団に適用すると，粒子はフェルミ統計に従うことが導かれる。ボーアの原子模型にパウリの原理を適用すると，D.I.メンデレーエフが経験的に発見した元素の周期律がみごとに説明でき，これは量子論の輝かしい成功の一つとなった。パウリの原理は固体の電子的性質にも重要な影響を与える。金属の磁性（強磁性，パウリ常磁性）や電気伝導はその顕著な例である。
執筆者：鈴木 勝久

出典　株式会社平凡社「改訂新版　世界大百科事典」

化学辞典 第2版

パウリの原理
パウリノゲンリ
Pauli's principle

パウリの排他原理ともいう．原子スペクトルの解釈においてきわめて重要な位置を占める原理で，量子力学が完全な形で定式化される以前に，1925年，W. Pauliによって見いだされた．それによると，同一原子内ではどの二つの電子も，そのすべての量子数が等しい値をとることはできない．これは量子力学の基礎理論からは導くことのできない一種の仮説であるが，この原理にもとづいて原子内の電子の状態や元素の周期律が明らかにされた．この原理は，多電子系の波動関数が満たすべき対称性に関する要請から導かれることが，のちにW.K. HeisenbergとP.A.M. Diracによって明らかにされ，“波動関数は電子座標の交換に関して反対称でなければならない”という，より一般的な形に定式化された．

出典　森北出版「化学辞典（第2版）」

百科事典マイペディア

パウリの原理【パウリのげんり】

排他律，禁制律とも。多数の電子からなる系では，１組の量子数によって確定される状態に電子は１個しか存在できないという法則。この原理を量子力学と組み合わせると，原子・分子の構造や周期律がよく説明される（原子構造）。一般に半整数のスピンをもつ粒子はパウリの原理に従い，フェルミ=ディラック統計によって扱われる（量子統計力学）。
→関連項目パウリ

出典　株式会社平凡社

ブリタニカ国際大百科事典 小項目事典

パウリの原理
パウリのげんり
Pauli's principle

排他律あるいは禁制原理などとも呼ばれる。 1925年に W.パウリにより提唱された。同一の状態に電子はただ1個しか入ることができないという形で表わされ，元素の周期律を説明するのに不可欠の原理である。多電子系の波動関数については，任意の2個の電子の位置座標およびスピンの交換に対して反対称であることを要求することで，パウリの原理が表わされる。この原理は電子ばかりでなく，一般に半奇数のスピンをもつフェルミオンに対しても適用される。

出典　ブリタニカ国際大百科事典 小項目事典

法則の辞典

パウリの原理【Pauli's principle】

すべての量子数が同一である状態を二個以上のフェルミ粒子＊がとることはできない．このフェルミ粒子は電子や中性子，陽子などである．電子が二つ以上ある系の波動関数は，任意の二つの電子の位置座標およびスピンの交換に関して反対称でなければならない．換言すると「二つ以上の電子の量子数がまったく一致することはない」ともいえる．パウリの排他律＊，パウリの禁制律，などとも呼ばれる．

出典　朝倉書店