改訂新版 世界大百科事典 「ベルヌーイ家」の意味・わかりやすい解説
ベルヌーイ家 (ベルヌーイけ)
The Bernoullis
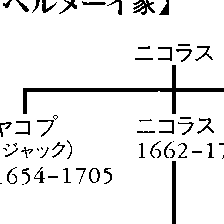
17世紀後半から約1世紀の間，図に示すように，多くの著名な数学者，物理学者を輩出したスイスの一族。その中でも，ヤコプJakob Bernoullis（1654-1705），ヨハンJohann B.（1667-1748），ダニエルDaniel B.（1700-82）の3人が有名である。なお，ドイツ名のほかヤコプはジャックJacques，ヨハンはジャンJean，ニコラスはニコラNicolasのフランス名も用いられた。ヤコプとヨハンの父は，ヤコプを神学者に，ヨハンを商人にしようと考えていたが，2人は父の意志に反してひそかに数学を勉強した。ヤコプは，バーゼル大学で神学を修めた後，数学の研究に転じ，1687年バーゼル大学の数学教授となる。ヨハンは商人に適さないことが明らかとなり，父の許しを得て，バーゼル大学で医学を修めた。兄ヤコプから数学の指導を受け，数学者に転向する。91年，パリに学んだヨハンは，そこでG.F.A.M.deロピタルの指導を受け，95年フローニンゲン大学の数学教授となる。兄ヤコプの死後は，バーゼルに帰りバーゼル大学教授となっている。
ヤコプとヨハンは，G.W.ライプニッツの微分積分の熟達者であり，微分積分学をニュートンとライプニッツの段階からさらに一歩進めこれを重要な諸問題に適用した。積分をcalculus summatoriesと呼ぶことをやめ，calculus integralisと呼ぶようになったのはヤコプに基づく（1690）。ヨハンはライプニッツと共に関数概念の形成に寄与している。ヤコプの著書《推論術》は彼の死後1713年に出版され，最終的にはニコラス・ベルヌーイがこの本の編集者であった。この中で，ヤコプは，特別の場合に，大数の弱法則を証明しており，それはヤコプ・ベルヌーイの名を，確率論史上，不朽のものとしている。《推論術》の中では実に多くの問題が論じられているが，破産問題もその一つである。それは確率過程の研究の端緒とみることもできる。さらに級数についても詳しく論じられている。すなわち彼は，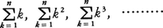
をnの多項式としてはっきり提示し，この計算をとおしてベルヌーイ数を発見した。また，無限級数
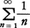の和が無限大であること（ヤコプはヨハンが最初に証明したと述べている），および級数
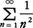が有限であることを証明している。しかしながら，後者の級数の和を求めることはできなかった。最速降下線の問題および等周問題は，ヤコプとヨハンの双方によって研究された。さらに，ヨハンは曲面上の2点を最短距離で結ぶ曲線，すなわち測地線を求める問題を提起した。これらの研究は，ヨハンの弟子L.オイラーに受けつがれ，変分学として発展し，解析力学の誕生に大きな影響を与えることになった。ヨハンは，微分方程式の求積法に関しても，多くの仕事をしている。今日，ベルヌーイの方程式として知られている微分方程式を論じ，かつ巧妙な方法で解いている。
ニコラスは2人の叔父ヤコプとヨハンの下で数学を研究した。彼の著作で出版されたものは，きわめて少なく，彼の業績の大部分は，他の数学者にあてた手紙の中にかくれているといわれている。ニコラスは，とくにモンモールP.R.Montmort（1678-1719）にあてた手紙で知られている。この2人の間の手紙（1710-12）の重要な部分は，モンモールの著書《偶然ゲームに関する解析の試み》第2版（1713）の中に記録されている。男女の出生率が，50:50でなく18:17であると仮定し，ヤコプの大数の法則を応用して，ロンドンの出生記録にあらわれた現象を説明したことが知られている。
執筆者：清水 昭信 ダニエルは1721年バーゼル大学で医学博士号を取得，その後25年から8年間ペテルブルグに滞在し，L.オイラーとともに数学，物理学の研究を精力的に行った。帰国後バーゼル大学の教授に就任するとともに，ペテルブルグ時代の研究を《流体力学》（1738）にまとめた。彼の研究は多岐に渡るが，歴史上有名なのは流体力学における二つの業績，すなわち分子運動論の立場に立った気体の諸性質の研究と，定常流に関するベルヌーイの定理の提出である。この研究は双方とも上記《流体力学》に収められている。ほかに呼吸，物体の振動，確率・統計，また，微積分学をはじめ数学自体の研究などにおいて第一級の業績を残し，パリのアカデミー・デ・シアンスから，10回にもわたって賞を受けた。これらの研究を背後で支えたモティーフを歴史的に評価すれば，それはさまざまな現象の機械論的説明と，その解析的形式化にあったといえよう。この意味で彼は，ニュートン力学の解析化，整備完成という18世紀的課題を切り開く先駆的存在であった。しかし，偏微分方程式の導入に伴う数理物理学の急速な発展に伍していくことはできなかった。
執筆者：橋本 毅彦
出典 株式会社平凡社「改訂新版 世界大百科事典」改訂新版 世界大百科事典について 情報