グラフ理論（読み）グラフリロン

デジタル大辞泉

グラフ‐りろん【グラフ理論】

いくつかの点（ノード）と、これらを結ぶ線分（エッジ）からなる図形の、位相幾何学的性質を解析する数学理論。歴史的には18世紀、レオンハルト＝オイラーの「ケーニヒスベルクの橋」という、七つの橋を1回ずつ渡って出発点に戻る道筋を考える問題に始まる。電気回路・交通問題・パズルなどに応用。

出典　小学館

精選版 日本国語大辞典

グラフ‐りろん【グラフ理論】

1. 〘 名詞 〙 ( グラフは[英語] graph ) 数学的理論の一つ。点や線分などをつなげて表わされるグラフについての理論。

出典　精選版 日本国語大辞典

日本大百科全書(ニッポニカ)

グラフ理論
ぐらふりろん

グラフ理論というときのグラフは、棒グラフや折れ線グラフ、また二次関数のグラフのように、量の変化を視覚的に表すときのグラフではない。たとえば鉄道網や道路網の図形を思い浮かべてみよう。そこでは現実の方位や距離などは無視され、かなり省略された図が描かれているのが普通である。それにもかかわらずその図が役にたつのは、必要とされる情報が、駅と駅とが何線で結ばれているかとか、乗り換えは何駅で行えばよいか、というようなことだからである。またたとえば会社の組織図や家系図、トーナメントの組合せ、電気回路の配線図なども同様の事情にある。そこで重要なのは、点で表されるもの（各部所、親や子、対戦相手、抵抗や半導体）の結合関係のみである。グラフ理論は、このような質的関係を表現し、研究する分野であり、応用領域は数学のみにとどまらず非常に広い。歴史的には後に述べるオイラーが出発点である。

　いくつかの点とこれらを結ぶ線分（曲線でもよい）からできる図形をグラフという。このとき点は頂点、線分は辺とよばれる。どの二つの頂点も、一方から出発して他方へと達する辺の列で結べるとき、そのグラフは連結であるという。連結なグラフは直観的には、ひとかたまりの図形をなしている。連結グラフのすべての辺を1回通るような周遊道が存在するかどうかという問題がある。これが18世紀に「ケーニヒスベルクの橋の問題」としてオイラーによって考えられた問題である。すなわち図Aのようなケーニヒスベルク（現、ロシア領カリーニングラード）のプレーゲル川に架かっていた七つの橋をすべて1回ずつ回って元の出発点に戻るような散歩道を考えよという問題である。オイラーは、町のA、B、C、Dの部分を頂点で、それらを結ぶ橋をこれらの点を結ぶ辺とみて、図Bのようなグラフを考えた。すると、散歩道をみいだす問題は、このグラフの周遊道をみいだす問題になる。オイラーは、「各頂点から出る辺の数がすべて偶数であるか、二つの頂点では奇数であるが他は偶数であるならば、連結グラフは周遊道をもつ」という定理を証明して、この問題に否と答えたのである。実際、この問題では各頂点から出る辺の数はすべて奇数である。したがってまた、AとBにもう1本の橋が架かっていれば（元の場所へは戻れないが）周遊道があり、さらにCとDにもう1本の橋が架かっていれば元に戻る周遊道が存在する。この定理はグラフの「一筆書きの定理」ともよばれ、逆も成り立つ。

　図Cのような正十二面体の各頂点を世界の都市とみて、各辺をそれらの間を行き来する旅行路としたとき、この旅行路に沿って各都市をちょうど1回通る世界旅行コースをみいだせというのがハミルトンの問題であり、旅行時間や旅費を考慮に入れれば旅行業者がいつも直面する問題でもある。この正十二面体の頂点のつくるグラフは、図Dのような平面上のグラフとなるので、このグラフの各頂点をちょうど1回通る通路を考えればよい。この場合には太線のような道が求める通路になる。同様な問題が任意の連結グラフで考えられるが、この一般の場合の解（一筆書きの定理のような）はまだ得られていない。

　グラフは、それらの辺が頂点以外では互いに交わることのないように平面に描けるとき平面グラフという。図Eのグラフを平面に描くと、かならずどれかの2辺が頂点以外の点で交わってしまうので、これは平面グラフではない。これに関してクラトウスキーによる、「グラフが平面グラフとなるためには、図Fの①または②のグラフが部分として含まれないことが必要十分である」という結果がある。

　グラフの一つの頂点から出る辺の個数をその頂点における局所次数という。頂点がA₁、A₂、…、Anであるグラフの各頂点Aiの局所次数がρ(Ai)であり、辺の数をNとするならば、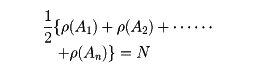

となる。このことから、局所次数が奇数であるような点はかならず偶数個あることがわかる。図Gのようなグラフは、閉じた道（ある点から出発して元に戻り、途中では自身と出会うことのない道）のないグラフであり、こうした連結グラフは英語のtreeを訳して木という。木はn個の頂点をもつとn－1個の辺をもつ。よって木の辺の個数をN、頂点の個数をnとすると、r＝N－n＋1＝0となる。しかし一般の連結グラフでは、この数r＝N－n＋1は0ではなく、このrをそのグラフの回路階数という（図H）。グラフの回路階数は、そのグラフに含まれる回路の数が多くなるほど多くなり、そのグラフの複雑さを示す数である。これは、この図形の一次元ベッチ数とよばれる位相不変量である。

　四色問題(よんしょくもんだい)（地図を国で色分けする場合、線で接する国を違う色で塗るとすると、必要な色の最大数は4である、ということの証明問題）も、各国を頂点に境界を接する国に対応する頂点を辺で結ぶと、頂点の彩色問題としてグラフ理論の一部とみられる。

［野口　廣］

『O・オア著、野口廣訳『グラフ理論』（1970・河出書房新社）』

[参照項目] | 一筆書き | 四色問題

グラフ理論（ケーニヒスベルクの橋の問題…

グラフ理論（ケーニヒスブルクの橋のグラ…

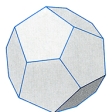
グラフ理論（正十二面体）〔図C〕

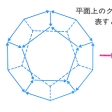
グラフ理論（正十二面体の頂点のつくるグ…

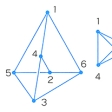
グラフ理論（どれかの2辺が頂点以外の点…

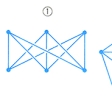
グラフ理論（平面グラフとなるための条件…

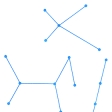
グラフ理論（閉じた道のないグラフ）〔図…

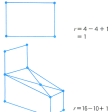
グラフ理論（グラフの回路階数）〔図H〕

出典　小学館　日本大百科全書(ニッポニカ)

改訂新版　世界大百科事典

グラフ理論 (グラフりろん)
theory of graphs

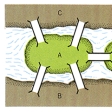
一筆書きの絵のように，いくつかの点とそれらを結ぶ線からなる図形がグラフである。線は何本あってもよく，曲がっていてもよいし長短もとわないことは電気系統の配線図と同様である。グラフを考えるときは，線のつながり方が重要であって形は問題としないが，線が余分に別な点を通るように変形したり，くぐらせるべきところを交わらせたりすれば別なグラフと考える。このようにグラフに対して許される変形を限定しておいて，それによって不変である性質を研究するのがグラフ理論である。考える対象を明確にするため，グラフは次の（1），（2）の性質をもつ点と線の集合であるとしよう（図1）。（1）もし二つの線に共通部分があれば，それは点であり，その点は構成要素となる。（2）構成要素である点は線の端点になっているか孤立点であるかのいずれかである。このとき点は頂点，線は辺または枝とも呼ばれる。グラフはそれに属するどんな2点をとっても，適当ないくつかの線をたどれば一方から他方に到達することができるとき連結であるという。どんなグラフもいくつかの連結したグラフ（部分グラフ）に分けることができる。

　グラフGの点aに連結している枝の個数をaの度数と呼びρ（a）と書く。Gの各点についての度数の総和をとれば，枝の個数の2倍になる。度数が奇数の点を奇点，偶数なら偶点という。度数の総和についての上の注意から，どんなグラフにおいても奇点の個数は0か偶数でなければならない。さらに連結グラフにおいては，奇点の個数が0か2であれば一筆書きができることが示される。一般に，奇点が2n個あるような連結グラフはn筆書きができる。その一筆の始めと終りは奇点である。また，もし二重の一筆書きを許すならば，連結グラフである限りそれはいつも可能である。

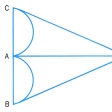
　グラフを連結した成分に分け，それぞれの構造をさらに詳しく調べるためには，いくつかの基本的な概念が必要となる。連結グラフで，頂点がすべて偶点ばかりであるものを閉列，二つだけが奇点であとの頂点はすべて偶点であるものを開列，両者をあわせて列trainという。開列の奇点は端点である。もし列の点の度数がすべて1か2ならばその列を路pathといい，それが閉列ならば閉路，開列ならば開路という。閉路はループと呼ばれることが多い（図2）。ループのない連結グラフが木tree（図3）でグラフ理論で重要な役割を果たす。各成分が木からなる非連結グラフは森と呼ばれることがある。木に属する任意の2頂点は一意的に定まる路で結ばれる。また，n個の点が与えられたとき，それらを頂点とするnⁿ⁻²個の異なった木が構成できる。一般に，木にはそれに属する特別な路で幹と呼ばれるものがあって，この木の任意の頂点はもっとも近いところにある幹の点と一路的に定まる路で結ぶことができる。このように木については組合せ論的な考察が容易となり，興味ある結果が知られている。連結グラフの部分グラフとしての木（部分木という）も考えられる。部分木が二つあればその共通部分もまた部分木になる。一方，連結グラフには極大な部分木が存在する（一意的とは限らない）。そして任意の頂点はどれかの極大な部分木に含まれる。極大部分木はその性質から知られるように応用上重要な役割を果たしている。このほか，グラフ理論では枝に向きを考えて電気回路網に応用したり，トポロジーの手法を用いたりしてその内容を豊富にしている。
執筆者：飛田 武幸

図1～図3

出典　株式会社平凡社「改訂新版　世界大百科事典」

ブリタニカ国際大百科事典 小項目事典

グラフ理論
グラフりろん
graph theory

グラフのもつ位相幾何学的な性質を解析する数学の一分野（→トポロジー）。ここでのグラフとは，折れ線グラフや棒グラフのような量の変化を図示したものではなく，一筆書きのように点と線との結合様式によって得られる図形である。たとえば，会社の組織図，トーナメントの組み合わせなどのように，線のつながり方によって得られる図形の本質（グラフ構造）を研究対象とする。有名な命題にケーニヒスベルクの橋の問題や四色問題がある。スイスの数学者レオンハルト・オイラーがケーニヒスベルクの橋の問題の解決法を与えるとともに，グラフ理論のもとをつくった。また 1930年代にハンガリーの数学者ポーリャ・ジェルジが現代数学のなかに位置づけた。（→離散数学）

出典　ブリタニカ国際大百科事典 小項目事典

百科事典マイペディア

グラフ理論【グラフりろん】

一筆書きの絵のように，いくつかの点とそれらを結ぶ線からなる図形がグラフである。線は何本あってもよく，グラフを考えるときは，線のつながり方が重要であって形は問題としない。線が余分に別な点を通るように変形したり，交わらないところを交わらせたりすれば，別のグラフと考える。このようにグラフに対して許される変形を限定しておいて，それによって不変である性質を研究するのがグラフ理論である。

出典　株式会社平凡社