チューリング機械（読み）チューリングキカイ（英語表記）Turing machine

デジタル大辞泉

チューリング‐きかい【チューリング機械】

⇒チューリングマシン

出典　小学館

改訂新版　世界大百科事典

チューリング機械 (チューリングきかい)
Turing machine

イギリスの数学者A.M.チューリングは1936年に発表した論文で，数学基礎論で当時懸案となっていた〈計算可能とはどういうことか〉という問題に対する一つの解答として，ある仮想的な機械を提案した。これが今日チューリング機械と呼ばれているものである。

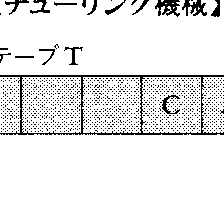
　チューリング機械は，図に示すように機械Mと両方向に無限にのびるテープTからなる一個の自動機械（オートマトン）である。テープは桝目に区切られており，そこには記号が1個書かれているか，何も書かれていない。機械Mはヘッドを持っており，テープ上を1桝目ごとに左右に移動し，テープに書かれた記号を読み，それを消し，あるいはそこに記号を書くことができる。機械Mは有限個の内部状態の任意の一つをとることができる。この内部状態の集合をQ＝｛q₀，q₁，q₂，……，q_n｝とする。テープにはいくらでも記号を書き込めるが，使用する記号の種類は有限である。この記号の集合をS＝｛s₀，s₁，s₂，……，s_n｝とする。

　チューリング機械の動作は，機械Mの現在の内部状態と現在読んでいる桝目の記号の二つで決められ，（1）機械Mの内部状態を変化させ，（2）その桝目に記号を書き込み，（3）ヘッドを左右いずれかへ1桝移動させる。チューリング機械の動作を関数で表すと，（1）f：Q×S→Q（状態遷移関数），（2）g：Q×S→S（出力関数），（3）h：Q×S→｛L，R｝（ヘッド移動方向の関数で，L（左），R（右）のどちらかをとることを示す）となる。すなわち，時刻tでMが内部状態q（t）にあり，読んでいる桝目の記号がs（t）のとき，時刻t＋1では状態f（q（t），s（t））に入り，その桝目にs（t）の代りにg（q（t），s（t））を書き込み，h（q（t），s（t））＝Lならヘッドを1桝だけ左へ，h（q（t），s（t））＝Rなら右へ動かす。

　一般に機械Mの動作は（q_i，s_j，f（q_i，s_j），g（q_i，s_j），h（q_i，s_j））なる“5文字組”の集合で定義される（このような機械を有限オートマトンという）。f（q_i，s_j）の定義されていない（q_i，s_j）の状況に到着したときにチューリング機械は“停止する”と定義しておく。またSには空白を表す記号bが必ず入っていて，空白の桝目にはbが書かれていると考える。

　さて，このように5文字組群で定義されたチューリング機械の“計算”は，まず，初期状態を与え，（空白を含む）記号列の書かれたテープを与え，最後にどの桝目から始めるかを定めることにより規定される。ヘッドは5文字組群に従って，自動的に1ステップずつテープ上の記号を処理していき，いつか停止するかまたは永久に動きつづける。停止したときは，そのときテープ上に書かれている記号列が初期テープ上の記号列に対する“計算”の答えである。

　チューリング機械は，5文字組群を変えることにより，さまざまな“計算”あるいは情報処理をすることができる。ただし問題ごとに情報をうまく記号列として与え，所要ステップ数が膨大になることは覚悟しなければならない。

　チューリングがコンピューターcomputer（文字通り“計算する人”）のモデルとしてこのような機械に想着したのは以下のような過程による。まず，人間の頭は有限の記憶能力しかない。紙の上に書かれた記号を読み，それに基本的な思考操作を加えて新しい記号を書く。“計算”とはこのような基本動作の繰返しである。そして，二次元状の紙の代りに一次元状のテープを使っても，計算可能という観点だけから見れば何ら支障はない。一時に読める記号数には限界があり，それを1個と限定しても支障はない。用いる記号もたかだか有限種類であるが，用紙はいくらでも補給されうる。以前に書いた記号は参照できるし，消して新しいものと書き換えてもよい。その後の計算可能性の理論や現代のコンピューターの発展を見ても，このチューリングの抽象化は正しかったといえる。他方，チューリングの時代に計算可能性に関していくつかの数学的提案があったが，これらはすべてチューリング機械と同等であることが証明された。そこで〈実際的な計算手続きと自然に呼べるいかなる過程もチューリング機械で実現可能である〉というチャーチA.Churchのテーゼが提唱されて現在に至っている。

　さて，チューリングは前記論文で万能チューリング機械が存在することをも証明した。この機械は，任意の与えられたチューリング機械（の5文字組群）を符号化してテープ上に与えられ，1ステップごとにこの記述を読みながらその動作を模擬するようなチューリング機械である。これは現代のコンピューターがプログラムを与えることによって何でも計算できるのと同一の考え方である。その反面，チューリング機械で計算（処理）不可能な問題が存在することも証明された。チューリングは，任意のチューリング機械に空白のテープを与えたとき，その機械が停止するか否かを決定するチューリング機械は存在しないことを示したのである。

　このようにチューリング機械の提案とそれによって発見された事実は数学基礎論に大きな影響を与えたばかりでなく，万能計算機の原理，プログラム，シミュレーションなど現在の計算機科学の理論的基礎を与えた。チューリング機械自体の研究もオートマトン理論が始まった1950年代から盛んになり，二次元状のテープを用いる変形や，計算に要するステップ数やテープの量などが問題となってきている。
執筆者：西尾 英之助

コラム－パリティーチェックをするチュー…

図－チューリング機械

出典　株式会社平凡社「改訂新版　世界大百科事典」

日本大百科全書(ニッポニカ)

チューリング機械
ちゅーりんぐきかい

イギリスの数学者チューリングが考えた、思考のうえでの計算機械である。これは、現在のコンピュータの理論的な原型であるともいえる。計算の理論を展開するための思考上の機械であるから、現実のコンピュータのように計算時間を短縮するための機構や結果を見やすくするためのプリンターなどはついていない。理論を展開するのに必要な最小限の部品しかついていない。

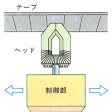
　チューリング機械は、(1)無限に長いテープ、(2)ヘッド、(3)制御部、の三つの部分だけから成り立っている。テープには、情報を格納することのできる区分があり、一つの区分の中に一つの記号を書き込むことができる。そしてこのテープは、左右の方向に無限に延びている。ヘッドは、テープの一つの区分に書かれている記号を読み取ったり、書き換えたりする。制御部は、ヘッドとの情報のやり取りをしたり、ヘッドの位置を動かしたりする部分である。制御部は、有限個の状態をもちうる。ヘッドで読み取った記号と、制御部の状態により、次に機械がなすべき動作が決まる。機械の動作の仕様は、次のような規則をいくつか書き並べて表すことにしている。「状態qのとき、ヘッドがテープから記号aを読み取ったら、zという作業をして、状態rへ移る」。ここでzには、次の3種類がある。(1)現在ヘッドがあるところのテープの区分の中にbという記号を書く（読み取った記号aは失われる）。(2)現在のヘッドの位置を右へ1区分だけ動かす。(3)現在のヘッドの位置を左へ1区分だけ動かす。

　テープに書き込んだり読み取ったりすることのできる記号は、有限個の種類しかないものとする。また、とりうる状態も、動作の仕様の規則も有限個に限る。このような機械に対して、次の四つを指定すると、この機械の動作が決まる。(1)利用するすべての記号、(2)とりうる状態、(3)この機械が始めにとる状態、(4)動作の仕様（規則の集まり）。

　チューリング機械は現実のコンピュータに比べると非常に簡単なものであるが、チューリングは、「ある問題を解くアルゴリズムが存在するということは、その問題がこの機械で解けることである」と定義した。アルゴリズムの存在の概念は、チューリングのほかに、クリーニStephen Cole Kleene（1909―1994）、ゲーデルや、チャーチAlonzo Church（1903―1995）、ポストEmil Leon Post（1897―1954）などが別々に考えていたが、のちになって、どれも同値の定義であったことが示された。チューリング機械の考え方は、現在のコンピュータ科学にとって重要な成果をもたらした。とくに、「チューリング機械で解けない問題が存在する」ことが証明されて、「アルゴリズムが存在しない問題がある」ことが明らかになった。つまり、このことはコンピュータに解けない問題があることを示している。

　あるチューリング機械の仕様をテープに書いておけば、その仕様の機械と同じ動きをするチューリング機械を万能チューリング機械という。これは、現在のプログラム内蔵方式のコンピュータと本質的に同じものである。万能チューリング機械は、チューリングのほか、高橋秀俊（1915―1985）、池野信一（1924―1988）、M・ミンスキー（1927―2016）など多くの人たちによって、簡素な仕様のものがつくられている。

［中西正和］

『M・ミンスキー著、金山裕訳『計算機の数学的理論』（1970・近代科学社）』▽『相沢輝昭著『計算理論の基礎』（1970・文一総合出版）』▽『小林孝次郎著『計算可能性入門』（1980・近代科学社）』

[参照項目] | アルゴリズム | 情報科学 | チューリング

チューリング機械

出典　小学館　日本大百科全書(ニッポニカ)

百科事典マイペディア

チューリング機械【チューリングきかい】

英国の数学者A.M.チューリングがデジタル計算機のモデルとして1936年に提唱した仮想的な機械。このモデルによれば，デジタル計算機で処理可能なことはチューリング機械の動作として記述可能であり，逆にチューリング機械で原理的に計算不可能な問題はデジタル計算機では処理できない。このようにチューリング機械の提唱とそれによって発見された事実は〈計算不能性〉をめぐって数学基礎論に大きな影響を与えたばかりでなく，万能計算機の原理，プログラム，シミュレーションなど，現在の計算機科学に理論的基礎を与えた。

出典　株式会社平凡社

世界大百科事典（旧版）内のチューリング機械の言及

【オートマトン】より

…たとえば，神経細胞網モデル，セルオートマトン，自己増殖オートマトン，などであり，その一部は今でも研究されている。計算機モデルとしては，これらよりも前に，チューリング機械があり，アルゴリズムや計算に関する研究がなされていた。　初期のころは，オートマトンさえ研究すればすべて解決するといったような楽観論が支配していたように思われる。…

【計算モデル】より

…コンピューターが行う計算を数学的に表したモデルのこと。計算モデルとしては複数の種類が提唱されているが，もっとも有名なのはA.M.チューリング が考案したチューリング機械である。チューリング機械は，有限状態の制御部と，左右無限に伸びたテープと，そのテープ上の記号を読み取るためのヘッドからなる(図)。…

【計算量】より

…そこで，アルゴリズム自体の効率を議論するために，ある程度抽象化された計算モデルを用い，そのうえでの計算時間を測る。　厳密な議論では，チューリング機械などの原始的な抽象機械を計算モデルとし，機械の計算ステップ数を計算時間とみなすのが一般的である。そこまで抽象化しなくてもよい場合には，プログラムの各単位実行文を1ステップとみなし，プログラムの実行に要したステップ数を計算時間としてもよい。…

【形式言語】より

…
[無制限文法]
　書き換え規則に対してどんな制約もおかない文法を無制限文法unrestricted grammar，あるいは0型文法という。この文法で生成される言語は無制限言語，あるいは0型言語といわれ，チューリング機械によって識別される。この言語の族は，前述の全ての言語の族を含む。…

※「チューリング機械」について言及している用語解説の一部を掲載しています。

出典｜株式会社平凡社「世界大百科事典（旧版）」