精選版 日本国語大辞典 「ドップラー効果」の意味・読み・例文・類語
ドップラー‐こうか‥カウクヮ【ドップラー効果】
日本大百科全書(ニッポニカ) 「ドップラー効果」の意味・わかりやすい解説
ドップラー効果
どっぷらーこうか
警笛を鳴らしながら列車が線路のわきに立つ観測者の前を走り過ぎると、そのとたんに警笛の音が低くなったように聞こえる。振動数ν0の音波を放つ音源と、この音を聴く観測者の、一方または両方が運動しているときには、観測者の聴く音の振動数νは、一般には音源の振動数ν0と同じ値をもたない。これを(音波の)ドップラー効果という。音源から観測者に向かう方向をn方向とする。観測者の速度uのn方向成分をun、音源の速度vのn方向成分をvnとし、静止座標系における音波の速度をcとする。二つの振動数の比は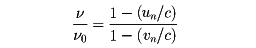
である。とくに、初めに記した例で、列車が近づいてくるときには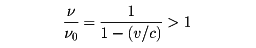
遠ざかるときには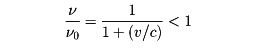
となる。
音源や観測者が運動しているときには、時間間隔(周期)T0ごとに音源から放たれた音波が観測者に届くまでに通過する距離が各周期ごとに一定量ずつ減るか増えるかするために、観測者の聴く音波の周期TはT0と同じではない。したがって、周期の逆数である振動数νとν0も異なる値をもつことになる。また、音源とともに運動する座標系、観測者とともに運動する座標系、および静止座標系で測った位置座標の間の関係は、ガリレイ変換によって与えられる。音源から放たれてn方向に伝わる音波の位相の式を三つの座標系について書くと、振動数の比ν/ν0の式が得られる。
まっすぐな道路を速度vで進む車から時間間隔T0を置いて次々に伝書鳩(でんしょばと)を放ち、この道路を速度uで先行する車を追わせる。伝書鳩の速度をcとする。先行する車には、時間間隔Tごとに伝書鳩が着く。TとT0の間には
vT0=c(T0-T)+uT
の関係がある。T0、Tの逆数をν0、νと書くと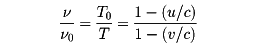
となる。前出の式はこれと同じ式である。
[飼沼芳郎]
光波のドップラー効果
特殊相対性理論の、ローレンツ変換を用いて論じられる。音波の場合との相違点は、どの座標系(慣性系)についても真空中の光速度c0が同一の値をもつことである。光源の座標系が、観測者の座標系に対して速度Vで並進運動をする場合には、光源の放つ振動数ν0の光波がn方向に進み、振動数νの光波として観測者に観測される。二つの振動数の比は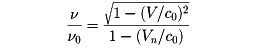
ここに、Vnは速度Vのn方向成分である。とくに、Vがnに平行の場合には
Vがnに反平行の場合には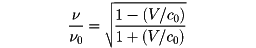
である。これらの比は、(V/c0)2が1に比して無視できる場合には、音波のドップラー効果の式と同じ形の式となる。これを縦のドップラー効果という。
Vがnに垂直のときには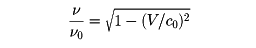
となる。この振動数の比は、Vが大きく、(V/c0)2が1に比して無視できぬ場合にだけ1と異なる値をもつ。これは光波にだけみられる効果で、横のドップラー効果とよばれる。この効果は、「走っている時計は遅れる」という特殊相対性理論でよく知られた現象の一例である。
[飼沼芳郎]
応用
オーストリアのJ・C・ドップラーが1842年にドップラー効果の着想を得たのち、音波や光波の分野でこの効果について数多くの研究が行われ、この効果はさまざまの方面に応用されてきた。気体の原子は走りながら光を放つ。気体原子の速度はマクスウェル分布に従っていろいろの値をとるので、ドップラー効果により、原子スペクトルの振動数は気体の温度に比例する幅にわたって分布する。これをスペクトル線のドップラー幅という。銀河系外の星雲の放つ光の連続スペクトルには数本の暗線(吸収線)が観察される。この暗線の振動数は、実験室内で観察される原子スペクトルの対応する線の振動数に比べると赤のほうに偏移している。ハッブルはこの赤方偏移がドップラー効果によって生ずると考えて、銀河系外の星雲は、遠方の星雲ほど大きな速度で遠ざかっているとし、宇宙は膨張しているという解釈に到達した。メスバウアー効果の実験では、無反跳γ(ガンマ)線の線源を一定速度で動かしたときにおこるγ線のドップラー効果が用いられる。路上を走行する自動車の速度の計測には、ドップラーレーダーが用いられ、センチメートル波の電波が車で反射したときのドップラー効果が利用されている。
[飼沼芳郎]
改訂新版 世界大百科事典 「ドップラー効果」の意味・わかりやすい解説
ドップラー効果 (ドップラーこうか)
Doppler effect
線路のそばで近づいてくる電車の警笛を聞くとき,電車が通り過ぎると急に音が低くなる。また電車に乗っていると,前方の踏切の警報機の音が,それを通り過ぎるとたんに低くなり,すれ違う電車の警笛の音も同様である。これらは日常しばしば経験することであるが,このように音源と観測者との一方,または両方が運動しているとき,観測者の聞く音の高さ(すなわち振動数)が変化する現象をドップラー効果という。1842年オーストリアの物理学者J.C.ドップラーが,二重星の光に関して,星の運動方向と色の変化(色の変化は振動数の変化による)を論じたのが発見の最初である。
静止している観測者に向かって,振動数f0(Hz)の音を発する音源が速さvs(m/s)で近づいてくる場合を考えよう。音の速さはv(m/s)とする。ある瞬間に音源から送り出された音波の山は1秒の間にvだけ進む。この間に音源もvsだけ進み,その間にf0個の音波の山を送り出す。したがって音源の進む方向ではv-vsの間に波の山がf0個あることになるので,波長はλ1=(v-vs)/f0となり,音源が静止している場合より短くなる。しかし波の進む速さは変わっていないので,観測者にとってその音の振動数は,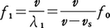 となる。すなわち,振動数が増えたことになり,実際の音源より高い音として聞こえる。音源が遠ざかる場合は,
となる。すなわち,振動数が増えたことになり,実際の音源より高い音として聞こえる。音源が遠ざかる場合は,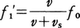 となる。
となる。
次に,音源が静止していて,これに向かって観測者がvO(m/s)の速さで近づく場合を考える。音源が静止しているので空間を進む音波の波長は変化せず,λ=v/f0である。しかし運動している観測者に対して波の山は速さv+vOで近づいてくる。その結果,観測者にとって波の振動数は,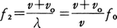 となる。音源も観測者も動く場合には,音源から観測者に向かう向きを正として速さvs,vOの符号をとると,上の二つの式を組み合わせて振動数は,
となる。音源も観測者も動く場合には,音源から観測者に向かう向きを正として速さvs,vOの符号をとると,上の二つの式を組み合わせて振動数は,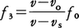 となる。
となる。
ドップラー効果は,音に限らずすべての波動現象に見られる。ただし光の場合には光速が非常に速いため,通常,ドップラー効果の影響はきわめてわずかであり,光源と観測者の相対速度が光速に比較できるほど十分に速い場合のみ観測される。星や星雲の中には,地球に対して視線方向に非常に大きな相対速度で遠ざかりつつあるものがあり,そのスペクトルを精密に観測すると,特定の原子の線スペクトルがドップラー効果によって赤の側(長波長側)にずれていることがわかる。これを赤方偏移といい,そのずれの大きさから,その星と地球の間の視線方向の相対速度を求めることができる。
マイクロ波のドップラー効果は航空機や自動車の速さの測定に応用されている。またレーザー光のドップラー効果を利用して,液体の流速を測定するドップラー流速計も実用化されている。
執筆者:有山 正孝
出典 株式会社平凡社「改訂新版 世界大百科事典」改訂新版 世界大百科事典について 情報
百科事典マイペディア 「ドップラー効果」の意味・わかりやすい解説
ドップラー効果【ドップラーこうか】
→関連項目アルゴス・システム|近接信管|シュタルク|速度計|フィゾー|流速計|流量計
出典 株式会社平凡社百科事典マイペディアについて 情報
ブリタニカ国際大百科事典 小項目事典 「ドップラー効果」の意味・わかりやすい解説
ドップラー効果
ドップラーこうか
Doppler effect
ドップラー効果[原子炉]
ドップラーこうか[げんしろ]
Doppler effect
出典 ブリタニカ国際大百科事典 小項目事典ブリタニカ国際大百科事典 小項目事典について 情報
法則の辞典 「ドップラー効果」の解説
ドップラー効果【Doppler effect】
光のドップラー効果は,光源と観測者との相対運動に基づくもので,シリウスのスペクトルについて1868年に観測されたのが最初といわれている.遠ざかる方向へ移動する光源からのスペクトル線は波長の長いほうにシフトして観測される(赤方偏倚*).これをもとに遠距離の銀河系の移動速度と距離との関係が求められた(ハッブルの法則*).
光のドップラー効果において,相対性理論に従うと,互いに v なる速度で移動する任意の二つの座標系 S,S′ において測定された振動数 ν,ν′ に対して
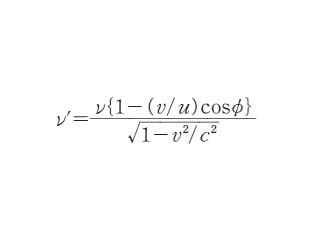
となる.ここで u は波動の位相速度,φ は光波の進行方向と観測者の移動方向とのなす角度である.
世界大百科事典(旧版)内のドップラー効果の言及
【ドップラー】より
…35年にはアメリカ移住を決意してミュンヘンまでいったが,結局プラハの州立中等学校の数学と会計学の教授職につき,その後41年には,プラハの国立工業大学に移り,基礎数学と実用幾何学の教授となった。42年に,《二重星と若干の他の天体の色光について》と題する論文を発表し,その中で観測される波の振動数が,波の伝搬する媒体に対する波源の運動や観測者の運動に関係すること,すなわちドップラー効果の存在を明らかにし,さらに46年の論文では,波源と観測者双方が同時に運動する場合へ拡張した。音に関するドップラー効果の検証は,1845年にオランダのバイス・バロットChristoph Hendrik Diederik Buys‐Ballot(1817‐90)がユトレヒトで,トランペッターをのせた機関車を使用して行った。…
【波動】より
…この電磁波によって単位時間,単位面積当りに運ばれるエネルギーの流れはポインティングベクトルで表される。
[ドップラー効果]
観測者と波源とが互いに近づく向きに運動しているとき,振動数が本来のものより大きく観測され,逆に互いに遠ざかる向きに運動しているときは小さく観測される。この現象も波動に特有のものでドップラー効果と呼ばれる。…
※「ドップラー効果」について言及している用語解説の一部を掲載しています。
出典|株式会社平凡社「世界大百科事典(旧版)」
関連語をあわせて調べる
春になって暖かくなりかけた頃、急に寒さが戻って、地面などがまた凍りつく。《 季語・春 》[初出の実例]「七瀬御秡 同晦日也。〈略〉雪汁いてかへる」(出典:俳諧・誹諧初学抄(1641)初春)...